Ménélaüs d'Alexandrie

Ménélaos ou Ménélaüs d'Alexandrie (fin du I^er siècle) est un mathématicien et astronome grec. Par analogie avec la propriété qu'ont les droites dans le plan, de déterminer le plus court chemin entre deux points, il introduisit la notion de géodésique sur la sphère.

Biographie

On sait par un dialogue de Plutarque, De facie in orbe lunæ, que Menelaüs passa une partie de sa vie à Rome, mais Pappus d'Alexandrie et Proclus laissent entendre qu'il avait étudié dans sa jeunesse à Alexandrie.

Ptolémée, au second siècle de notre ère, dit également dans son Almageste (chap. VII.3), que Ménélaüs observa deux occultations des étoiles α Virginis (Spica) et β Scorpii par la Lune à Rome en janvier 98, à seulement quelques jours d'intervalle. Pour Ptolémée, elles confirmaient la précession des équinoxes, un phénomène découvert par Hipparque au deuxième siècle av. J. C.

Les Sphériques est le seul traité de Ménélaüs qui soit parvenu jusqu'à nous, et cela par une traduction arabe. Ces trois livres traitent de la géométrie de la sphère et de ses applications à l'astronomie. C'est ce traité qui définit le triangle sphérique comme formé par trois arcs de grands cercles, les trilatéraux, et qui contient le théorème suivant, dit théorème de Ménélaüs, étendu aux triangles sphériques.

Théorème de Menelaüs dans le plan

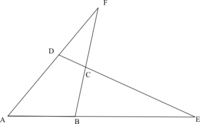
Ce théorème énonce que, les trois points C, D, E appartenant respectivement aux droites (BF), (AF), (AB), tout en étant distincts de A, B, et F, il est équivalent de dire :

1. 
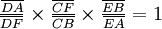
2. C, D, E sont alignés

On appelle transversale du triangle ABF toute droite qui, comme ici CDE, coupe les trois droites (BF), (AF), (AB) sans intercepter les sommets A, B, F.

Œuvres

On connaît par une tradition indirecte les titres de quelques traités de Ménélaüs :

• Les sphériques en trois livres, traduit en arabe par Hunayn ibn Ishaq en 910. Ce traité fut traduit en latin par Gérard de Crémone, puis Francesco Maurolico et enfin par Edmund Halley.
• Des cordes dans le cercle, en six livres, était connu de Théon d'Alexandrie
• Éléments de géométrie en 3 livres, traduits en arabe par Thabit ibn Qurra
• De cognitione quantitatis discretæ corporum permixtorum contenait, selon la tradition arabe, des expériences de pesée avec une balance hydrostatique.
• Menelaüs a peut-être également tenu un catalogue d'étoiles.

Bibliographie

• Björnbo, A. A., Studien über Menelaos' Sphärik. Beiträge zur Geschichte der Sphärik und Trigonometrie der Griechen, Abhandlungen zur Geschichte der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen, vol. 14, Leipzig 1902 ; voir aussi le Dictionary of Scientific Biographies, vol. IX, pp. 296-302.
• Thomas Heath - "A history of Greek mathematics" vol. 2 (1921, rééd. 1981), éd. Dover. ISBN 0-486-24074-6
• Krause, M., Die Sphärik von Menelaos aus Alexandrien in der Verbesserung von Abu Nasr Mansur b. `Ali b. `Iraq, mit Untersuchungen zur Geschichte des Textes bei den islamischen Mathematikern, Abhandlungen der Gesellschaft der Wissenschaften zu Göttingen, Philologisch-historische Klasse, 3e série, n° 17, Berlin 1936
• Y. et R. Sortais - La géométrie du triangle (1987), éd. Hermann
• TAHA A.-K. ; PINEL P.; "Sur les sources de la version de Francesco Maurolico des Sphériques de Ménélaos", Bollettino di storia delle scienze matematiche ISSN 0392-4432 ,1997, vol. 17, no2, pp. 149-198
• PINEL Pierre; TAHA Abdelkaddous; "Le travail d'al-Tusi sur les Sphériques de Ménélaos : établissement critique du texte, apport mathématique, interprétation astronomique "; Farhang, vol. 15-16, n° 44-45, pp. 33-109
• NADAL Robert; TAHA Abdelkaddous ; PINEL Pierre, "Le contenu astronomique des Sphériques de Ménélaos", Archive for history of exact sciences ISSN 0003-9519,2004, vol. 58, no5, pp. 381-436
• Pierre PINEL ; A. K. TAHA; "L'historique des Sphériques de Ménélaos de l'Antiquité à nos jours (Partie 1)", Mirror of Heritage, Ayene-ye Miras, New Series, vol. 3, Issue n° 1, (28), Spring 2005, pp. 45-68

Liens externes

• Le théorème de Ménélaüs (démonstration interactive)

• Portail de l’astronomie
• Portail de la géométrie