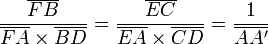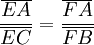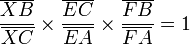Théorème de ménélaüs

Théorème de Ménélaüs

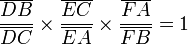
Le théorème de Ménélaüs d'Alexandrie affirme que si D, E et F sont trois points des côtés (BC), (AC) et (AB) d'un triangle ABC, alors D, E et F sont alignés si et seulement si :: $\frac{\overline{DB}}{\overline{DC}}\times \frac{\overline{EC}}{\overline{EA}} \times \frac{\overline{FA}}{\overline{FB}} = 1$

Une telle droite est appelée une ménélienne du triangle ABC.

Démonstration du théorème de Ménélaüs

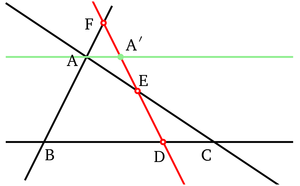
Soient D, E, et F trois points alignés appartenant aux côtés (BC), (AC) et (AB) d'un triangle. Introduisons A' le projeté de A sur (EF) parallèlement à (BC) ; A' est simplement le point d'intersection de la droite (EF) avec la parallèle à (BC) passant par A.

D'après le théorème de Thalès appliqué aux triangles FBD et EDC, on a respectivement

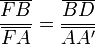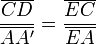
$\frac{\overline{FB}}{\overline{FA}} = \frac{\overline{BD}}{\overline{AA'}}$ et $\frac{\overline{CD}}{\overline{AA'}} = \frac{\overline{EC}}{\overline{EA}}$

en mesures algébriques. On en déduit que

$\frac{\overline{FB}}{\overline{FA} \times \overline{BD}} = \frac{\overline{EC}}{\overline{EA}\times \overline{CD}} =\frac{1}{\overline{AA'}}$

ce qui équivaut à

$\frac{\overline{DB}}{\overline{DC}}\times \frac{\overline{EC}}{\overline{EA}} \times \frac{\overline{FA}}{\overline{FB}} = 1$

Réciproquement, soient DEF trois points appartenant respectivement aux côtés (BC), (AC) et (AB) d'un triangle et tels que

$\frac{\overline{DB}}{\overline{DC}}\times \frac{\overline{EC}}{\overline{EA}} \times \frac{\overline{FA}}{\overline{FB}} = 1$

Supposons d'abord que (EF) et (BC) soient parallèles. En appliquant le théorème de Thalès dans le triangle ABC, on aurait

$\frac{\overline{EA}}{\overline{EC}} = \frac{\overline{FA}}{\overline{FB}}$

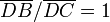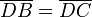Compte tenu de l'hypothèse, cela implique que ${\overline{DB}}/{\overline{DC}}=1$ soit $\overline{DB} = \overline{DC}$ , donc on aurait B=C ce qui est impossible. On en déduit que (EF) et (BC) sont sécantes et on appelle X leur point d'intersection.

Comme démontré plus haut, on a

$\frac{\overline{XB}}{\overline{XC}}\times \frac{\overline{EC}}{\overline{EA}} \times \frac{\overline{FB}}{\overline{FA}} = 1$

et d'après l'hypothèse, on a donc 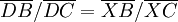${\overline{DB}}/{\overline{DC}}={\overline{XB}}/{\overline{XC}}$ ce qui implique X=D. Les points D, E et F sont donc alignés.

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de M%C3%A9n%C3%A9la%C3%BCs ».

Catégories : Théorème de géométrie | Géométrie du triangle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de ménélaüs de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Theoreme de Menelaus — Théorème de Ménélaüs Le théorème de Ménélaüs d Alexandrie affirme que si D, E et F sont trois points des côtés (BC), (AC) et (AB) d un triangle ABC, alors D, E et F sont alignés si et seulement si :: Une telle droite est appelée une… … Wikipédia en Français
Théorème de Menelaüs — Théorème de Ménélaüs Le théorème de Ménélaüs d Alexandrie affirme que si D, E et F sont trois points des côtés (BC), (AC) et (AB) d un triangle ABC, alors D, E et F sont alignés si et seulement si :: Une telle droite est appelée une… … Wikipédia en Français
Théorème de Ménélaüs — En mathématiques, et plus précisément en géométrie, le théorème de Ménélaüs, dû à Ménélaüs d Alexandrie, affirme que si D, E et F sont trois points des côtés (BC), (AC) et (AB) d un triangle ABC, alors D, E et F sont alignés si et seulement… … Wikipédia en Français
Théorème de Céva — Théorème de Ceva Pour les articles homonymes, voir Ceva (homonymie). Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si … Wikipédia en Français
Théorème de ceva — Pour les articles homonymes, voir Ceva (homonymie). Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si … Wikipédia en Français
Menelaus — Ménélaüs d Alexandrie Ménélaos ou Ménélaüs d Alexandrie (fin du Ier siècle) est un mathématicien et astronome grec. Par analogie avec la propriété qu ont les droites dans le plan, de déterminer le plus court chemin entre deux points, il… … Wikipédia en Français
Menelaus d'Alexandrie — Ménélaüs d Alexandrie Ménélaos ou Ménélaüs d Alexandrie (fin du Ier siècle) est un mathématicien et astronome grec. Par analogie avec la propriété qu ont les droites dans le plan, de déterminer le plus court chemin entre deux points, il… … Wikipédia en Français
Ménélaus d'Alexandrie — Ménélaüs d Alexandrie Ménélaos ou Ménélaüs d Alexandrie (fin du Ier siècle) est un mathématicien et astronome grec. Par analogie avec la propriété qu ont les droites dans le plan, de déterminer le plus court chemin entre deux points, il… … Wikipédia en Français
Ménélaüs — d Alexandrie Ménélaos ou Ménélaüs d Alexandrie (fin du Ier siècle) est un mathématicien et astronome grec. Par analogie avec la propriété qu ont les droites dans le plan, de déterminer le plus court chemin entre deux points, il introduisit… … Wikipédia en Français
Ménélaüs d'Alexandrie — Ménélaos ou Ménélaüs d Alexandrie (fin du Ier siècle) est un mathématicien et astronome grec. Par analogie avec la propriété qu ont les droites dans le plan, de déterminer le plus court chemin entre deux points, il introduisit la notion de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de ménélaüs