- Mouvement De Lagrange De La Toupie
-
Mouvement de Lagrange de la toupie
Le mouvement de Lagrange de la toupie est le mouvement d'une toupie pesante autour d'un point O de son axe, la réaction d'axe n'ayant pas de moment par rapport à O (rotule parfaite).
C'est à peu près le mouvement d'une toupie ordinaire, à ceci près que dans une toupie , le clou de la toupie est rond et glisse en frottant sur le plan où elle "repose" : il s'ensuit par application du théorème du couple gyroscopique qu'elle se redresse et vient en position de toupie dormante.
Le cas de Lagrange est mieux visualisé par le mouvement d'un gyroscope à deux axes de Cardan, surchargé : si la rotation est très rapide, la précession est directement proportionnelle au poids. On a donc une balance gyroscopique! Il convient d'étudier d'abord ce cas plus facile, avant d'aborder le cas général.
Sommaire
Balance gyroscopique : Précession = ~ mga/Cr(0)
- Description géométrique : on adopte les conventions suivantes pour les angles d'Euler: la rotation du premier cardan est définie par l'angle ψ(t) ; la rotation du deuxième cardan, intérieur au premier est la nutation
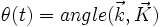 ; la toupie est enfin mobile autour de son axe de révolution O,K, selon l'angle de rotation propre φ(t) .
; la toupie est enfin mobile autour de son axe de révolution O,K, selon l'angle de rotation propre φ(t) . - Description cinématique : soit O, u l'axe des nœuds. le vecteur rotation est donc :
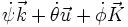
- Description cinétique : les inerties à la rotation propres sont A, A, C ;
l'énergie cinétique.2 est donc
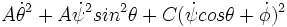
- Description dynamique :
le théorème du moment cinétique écrit selon u, K/\u, K donne les trois équations :
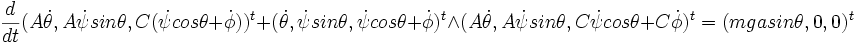
- Intégration dans l'approximation gyroscopique (vitesse de rotation propre très grande):
la troisième équation donne Lz = =cste = Cr(0) =~ C
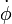 .
.La deuxième équation donne θ = θ0 = cste : la nutation est constante.
La première équation donne
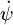 = mga / Cr(0).
= mga / Cr(0).La précession « pèse » donc linéairement sur mga, indépendamment de la nutation.
On peut aussi considérer que cela n'est qu'artificiel, car le moment est en sinθ : alors , il est plus naturel de considérer le couple M et écrire
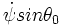 = M / Cr(0):= Précession := Pr en rad/s
= M / Cr(0):= Précession := Pr en rad/s- Retrouver cela par le théorème du couple gyroscopique:
Cr(0)dK/dt = M= mga k/\K ; soit Cr(0).Pr.K/\k +mga k/\K = 0
Précession des équinoxes d'Hipparque
Cette fois, le moment M est celui du soleil sur le renflement équatorial. Soit Q le quadrupôle terrestre = 2(A-C)<0 : M = 3/4
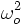 .cosθ.Q.k/\K (cf gravimétrie):
.cosθ.Q.k/\K (cf gravimétrie):- Précession = -
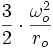 .cos
.cos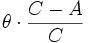 .
.
De la valeur de la précession (26 000 ans), on tire la valeur de (C-A)/C de la Terre.
En réalité, il faut aussi tenir compte de l'influence de la Lune : celle-ci intervient environ par le double (mais, inversement, la Lune subit le moment en retour, alors que le Soleil qui le subit aussi est influencé de façon négligeable suite à sa masse) : au 16"/an s'ajoutent donc 34"/an dus à la lune, soit 50"/an, soit un tour en 26 000 ans :
Hipparque ne savait pas mesurer le point Gamma avec la précision de 1" d'arc, mais il disposait des mesures antérieures vieilles de 2 siècles, soit 10 000" d'arc, ce qui suffisait.
Le pôle céleste n'est pas éternellement voisin de l'étoile polaire. En 26 000 ans, il décrit dans le ciel un cercle autour du point Q, de direction perpendiculaire à l'écliptique, point Q situé environ au milieu du Dragon (regarder sur un globe céleste le cercle écliptique (le Zodiaque suffit) et prendre la perpendiculaire à cet anneau) : le cercle de 23°26' est très large et emmènera dans 13 000 ans le pôle vers la constellation du Cygne (à vérifier!) : alors du point de vue climat, l'hémisphère nord recevra cette fois un peu plus de chaleur que l'hémisphère sud (~ 7%), ce qui est important dans la théorie de Milancovitch du climat (il faut y rajouter la variation périodique d'excentricité e(t) et la variation périodique d'inclinaison i(t) (stabilisée par l'existence de la Lune!) On obtient ainsi une remarquable concordance avec les cycles glaciaires de l'holocène.
A noter que le plan orbital de la Lune est décalé par rapport à l'équateur terrestre et l'écliptique; il en résulte un léger décalage de 9" d'arc et une période d'1 saros ( 18.6 ans); cet effet est négligeable sur le climat , certes!
Mouvement linéarisé
Reprendre les 3 équations exactes; et injecter les approximations suivantes :
- θ(t) = θ0 + Y(t)
- ψ(t)sinθ0 = t.Pr + X(t) , avec Pr = M/Cr(0)
et linéariser en (X,Y):
- X" + Pr².X + Y'. Couplage = 0
- -X'. Couplage + Y" = 0
avec Couplage = constante = (Cr(0)-2A.Pr.cosθ0)/A, pratiquement égal à C/A r(0) en rad/s, caractérisant le couplage gyroscopique, qui conserve l'énergie : celle-ci ne peut que se tranférer de X vers Y et réciproquement.
La deuxième équation s'intègre immédiatement : -X . Couplage + Y' = constante = a
Soit X" + X(Pr² + Couplage²) + a.Couplage = 0
on trouve donc X(t) = cste + oscillation de pulsation = sqrt(Pr² + Couplage²) ~ Couplage = C/A r(0)
et Y(t) = b .t + oscillation de même pulsation .
On reconnaît le dessin d'une trochoïde plus ou moins allongée dessinée sur la sphère unité par le vecteur K : les pointes de la cycloïde sont toujours vers le haut (faire attention en projection horizontale selon que θ0 > ou < π / 2).
- Application : m = 1kg; OG = a = 2cm ; A = m r² avec r = 4cm et C=mr'² avec r'= 3.6 cm (toupie-prolate); theta(0) = 30° ; r(0) = 4500 tours/minute donne :
theta-max -theta(0) = 3' ; nutation de période = 10 ms ; précession = 14°/s .
Mouvement de Lagrange général
C'est évidemment plus compliqué si tous les OdG (Ordre de grandeur) se recoupent!
On peut montrer qu'il s'agit d'un mouvement à la Poinsot dans un référentiel bougeant à la Poinsot : il ne reste plus qu'à se représenter mentalement le mouvement.
Plus concrètement, le mouvement est intégrable, car il existe trois intégrales premières : puisque M = k/\K , L.k = constante = L1; L.K = constante = L2 et l'énergie E = 1/2L.ω + mga.cosθ.
Quelques calculs donnent une équation de Newton (voir diagramme horaire); donc le mouvement est intégrable à une quadrature près : E = 1/2 A
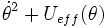 , avec Ueff = mga.cosθ + L2²/2C + (L1-L2.cosθ)²/2(A.sin²θ).
, avec Ueff = mga.cosθ + L2²/2C + (L1-L2.cosθ)²/2(A.sin²θ).On doit distinguer en mathématiques 8 cas possibles. Mais pas en physique (voir pendule simple).
La discussion s'effectue essentiellement selon 2 grands cas possibles: pour theta = 0, Ueff(0) est infinie ou bien finie (ce qui exige la condition "impossible" en physique : L1 = L2); ensuite, dans le cas Ueff(0) finie, il reste à distinguer si exprimée en fonction de cos(theta), il y a minimum ou non. Les "bifurcations" et les séparatrices dans l'espace des phases ne sont vraiment sensibles qu'à l'œil exercé de qui veut bien regarder le détail de tout mouvement de cette toupie.
Œuf de Christophe Colomb : L²/4A > mga
Dans ce dernier cas, on trouve que si L1=L2 est suffisamment grand, la position verticale de la toupie est stable : L²/4A > mga est la condition dite de Colomb : la légende veut que Colomb prît un œuf (cuit) et le fît tenir vertical en le faisant tourner rapidement sur une table.
Si L1 différent de L2, il est facile de montrer que theta reste bloqué entre deux valeurs: les valeurs de théta inférieures à 90° sont dues , on s'en doute , à l'effet gyroscopique. Quand r(0) n'est plus suffisant, theta reste toujours bloqué entre deux valeurs (donc theta = 180° est impossible: c'est l'objet de multiples jeux de foire ; déquiller la quille du centre est impossible avec un pendule gyroscopique). Inversement un pendule gyroscopique lancé verticalement aura du mal à changer sa position verticale, et répondra moins que le simple pendule sphérique aux perturbations extérieures.
Précession uniforme
Comprendre que cette condition impose nutation nulle doit maintenant être assez intuitif. Et la vitesse de précession Pr est donnée par la formule :
- L2.Pr - A. Pr². cosθ = mga
Ce qui peut se retrouver géométriquement :
Le vecteur K subit une précession sans nuter, (donc L est aussi en précession, sans nuter), autour de la verticale (on dit que la toupie ronfle; on dit qu'elle dort si theta est nul). Le moment dynamique est Pr k/\L = u [L2.Pr -A Pr².cos(theta)].sin(theta)et est égal à M = u mga.sin(theta) cqfd.
Les forts en mécanique pourront aussi appliquer le cours :
sachant que r =
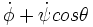 , on peut écrire directement :
, on peut écrire directement :0 = couple gyro +couple de déséquilibrage dynamique + M , soit :
0 = -C
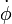 .Pr.sinθ - (1/2).(C-A)Pr².sin2θ +mga.sinθ
.Pr.sinθ - (1/2).(C-A)Pr².sin2θ +mga.sinθC'est bien le même résultat Ce résultat exact précise celui trouvé pour la balance gyroscopique.
Voir aussi
Articles connexes
- Mouvement à la Poinsot
- pendule gyroscopique
- balance gyroscopique
- compas gyroscopique
- gyroscope
Liens externes
Il existe bien d'autres cas de l'intégrabilité du mouvement du solide autour d'un point : un travail très approfondi se trouve sur la toile (rechercher Kovaleskaia et Goritchev). On citera seulement un article de vulgarisation : [1]
Pour plus, se référer à l'ouvrage Systèmes intégrables de Michèle Audin, dans lequel elle présente différents résultats sur la théorie de l'intégrabilité, laquelle a fait de notables progrès durant les deux dernières décennies.
- Portail de la physique
Catégories : Article à recycler (physique) | Dynamique du solide - Description géométrique : on adopte les conventions suivantes pour les angles d'Euler: la rotation du premier cardan est définie par l'angle ψ(t) ; la rotation du deuxième cardan, intérieur au premier est la nutation
Wikimedia Foundation. 2010.
