Mouvement a la Poinsot

En mécanique du solide, on appelle mouvement à la Poinsot, le mouvement d'un solide autour de son centre de gravité G, le moment des forces extérieures par rapport à G étant nul. Il existe 3 cas :

• le solide a ses inerties de rotation égales : A = B = C = J. Alors le mouvement se réduit à une simple rotation uniforme d'axe le moment cinétique Lo (constant), à la vitesse angulaire Lo/J , donc d'énergie cinétique constante Lo²/2J.
• le solide est à symétrie de révolution : on parle de mouvement d'Euler-Poinsot de la toupie. Le mouvement de la Terre en est un exemple.
• le solide est quelconque : le mouvement est périodique, intégrable grâce aux fonctions elliptiques de Jacobi (voir pendule simple) : c'est le mouvement à la Poinsot.

Sommaire 1 Mouvement d'Euler de la toupie 2 Démonstration du théorème d'Euler 3 Exemple de la Terre 4 Mouvement à la Poinsot 5 Voir aussi 5.1 Articles connexes 5.2 Liens externes

Mouvement d'Euler de la toupie

Soit un solide de révolution S, d'axes principaux I, J , K, d'inertie à la rotation (A, A, C).

Soit Gz la direction du moment cinétique constant Lo.

Soit GP = 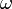(t).

Soient S la projection de P sur Gz , et R la projection de P sur GZ (d'axe K).

Théorème d'Euler : la figure GS, GP, GR tourne en bloc autour de Gz sans se déformer : l'angle de nutation (Gz, GZ)= θ reste constant. Le mouvement de (S) est donc simplement le mouvement de rotation sans glissement du cône de révolution d'axe GZ, de génératrice GP, sur le cône de révolution d'axe Gz (Lo), de génératrice GP : l'herpolhodie (lieu de P dans le référentiel barycentrique) est donc le cercle de centre S de rayon SP ; et la polhodie (lieu de P dans le référentiel propre du solide (S)) est le cercle de centre R de rayon RP.

L'angle de précession varie linéairement : 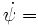Lo/A (= PR/sinθ).

L'angle de rotation propre varie linéairement : 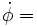Lo cosθ(1/C-1/A)

Démonstration du théorème d'Euler

• lemme 1 : GP appartient au plan Gz, GZ : en effet la matrice est de révolution.
• lemme 2 : l'angle de nutation est constant : en effet d/dt(Lo.K)= Lo.(ω×K) = 0 par le lemme 1.
• lemme 3 : OR := r = 1/C . Lo.K = cste via le lemme 2.
• lemme 4 : 2Ec = cste = OP.Lo donc OS est constant.
• lemme 5 : décomposer OP (et non pas projeter) sur Gz et GZ : on trouve aisément précession et rotation propre.

Exemple de la Terre

Dans le cas de la Terre, bien dessiner la figure, car C > A : GP est extérieur à l'angle (GR, GS);

D'autre part, la Terre est essentiellement un géoïde de forme ellipsoïdale aplatie, avec A/(C-A) = 305. (S'il s'agissait d'un ellipsoïde homogène, on aurait A/(C-A)= (a²+c²)/(a²-c²)=~297 : la Terre est plus dense au centre); le mouvement de précession est de période 305,(365/366)jours ; le mouvement de rotation propre est de 86 164,1 s. Au pôle Nord, la polholdie est un cercle d'environ 10 m : c'est dire que le vecteur rotation et le moment cinétique sont quasi-alignés. Ce mouvement, à peine perçu à la fin du XIX^e siècle (par Chandler), est maintenant très bien suivi par l'IERS.

Note : cette description, dite d'Euler, ne correspond pas à la réalité expérimentale observée par l'IERS :

1. la Terre n'est pas de révolution.
2. Surtout la Terre n'est pas un solide : il existe des tremblements de Terre (voir effet Sumatra), des mouvements de convection profonde correspondant à la tectonique des plaques, un noyau dont une partie est liquide et agité de mouvements de convection importants (voir géomagnétisme terrestre); enfin et surtout, la Terre se comporte comme un matériau doué d'élasticité et de viscosité; le rebond glaciaire relève le bouclier canadien, entraînant une dérive de la polhodie ; de plus, le mouvement des océans (courants et marées) et le mouvement de l'atmosphère perturbe la polhodie (voir rotation de la Terre).
3. le moment cinétique Lo de la Terre n'est pas constant. À cause du bourrelet équatorial, il subit une précession , dite précession des équinoxes, déjà décrit par Hipparque (200 av. J.-C.).

Mouvement à la Poinsot

Géométriquement, le mouvement à la Poinsot est décrit comme suit :

Soit l'ellipsoïde E1 respectant A X² + B Y² + C Z² = 1 et soit l'ellipsoïde E2 respectant A² X² + B² Y² +C² Z² = Lo²/2Ec . Le vecteur OP est à l'intersection de ces deux ellipsoïdes : la polhodie est donc la courbe du 4^e ordre tracée sur E1 et E2.

On convient de prendre A > B > C : éliminer y et constater que la projection de la polhodie est A(A-B)X² + C(C-B)Z² = constante - C : ce sont donc des arc d'hyperboles ayant les mêmes asymptotes, avec 2 cas de dégénérescence : l'un est trivial : les axes GZ et GX recoupent l'ellipsoïde en deux ellipses; l'autre est aussi l'intersection de 2 ellipses.

On voit donc que les polhodies sont des courbes fermées appartenant à 4 quadrants distincts et symétriques : on peut, grosso modo, dire qu'il y a deux types de mouvement : un mouvement autour de l'axe GZ (celui de la longueur de la boîte d'allumettes), et un mouvement autour de la perpendiculaire à la face de la boîte d'allumettes (qui est, quand on a fait beucoup ricochets sur l'eau avec des pierres, le plus « stable »), et il n'y a aucun espoir de lancer la boîte selon l'axe perpendiculaire aux « grattoirs » : c'est bien une position du mouvement stationnaire , mais elle est instable!

Les herpolhodies sont évidemment plus compliquées, puisque le plan tangent en P au premier ellipsoïde (E1) coupe la podaire de G en S ; et GS est un vecteur fixe du référentiel barycentrique, car GS a pour direction Lo et pour valeur 2Lo²/Ec : l' « œuf » (E1) roule donc autour du point G en restant en contact avec le plan perpendiculaire en S à GS au Point qui décrit sans glisser une herpolhodie sans point d'inflexion.

On peut évidemment écrire les équations d'Euler du mouvement :

A p' + ( C-B) qr = 0 (et 2 autres par permutation)

Soit pqr dt = ds une nouvelle échelle de temps :

Ap² = 2(B-C) (s-s1) et idem pour q(t) et r(t).

Il en résulte donc que dt = K .ds / sqrt[(s-s1)(s-s2(s-s3)]: s(t) est donc une « simple » intégrale elliptique. De manière plus immédiate, on peut dire que le système des 3 équations d'Euler avec les 3 conditions initiales [p(0), q(0), r(0)] définit 3 fonctions p(t), q(t) et r(t) qui sont directement liées aux fonctions de Jacobi : sn(t) , cn(t) et dn(t).

Remarque : le mouvement , ayant lieu à énergie constante, est évidemment infini : ce que dit Poinsot est qu'il est périodique dans S : les polhodies sont fermées , de période finie (sauf dégénérescence exceptionnelle du temps infini en direction de l'axe Oy).

Comme il y a toujours une petite perte d'énergie, il convient d'examiner la stabilité des 3 points fixes que sont les trois axes. Finalement, l'axe le plus stable est l'axe Ox (celui, banal, du « ricochet »).

Remarque : il est intéressant d'examiner le cas dit « gyroscopique », où p >> q et p >> r : alors la figure GPS est très étroite, et les fonctions de Jacobi s'approximent très bien par des fonctions sinusoïdales.

Voir aussi

Articles connexes

• Pendule simple
• Mouvement de Lagrange de la toupie

Liens externes

• Article [pdf]

• Portail de la physique