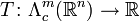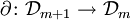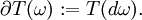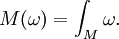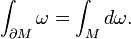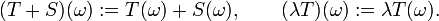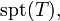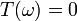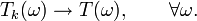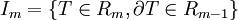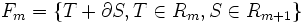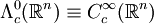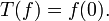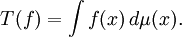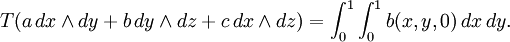Courant (Mathématiques)

Courant (mathématiques)

Sommaire

1 Introduction
2 Topologie
3 Cas particuliers
4 Exemples
5 Bibliographie

Introduction

En mathématiques, et plus précisément en analyse fonctionnelle et en topologie différentielle, un courant selon Georges de Rham est une fonctionnelle sur l'espace des formes différentielles à support compact d'une variété différentielle. En fait, les courants peuvent être vu comme une extension des distributions. Sur le plan géométrique, ils peuvent correspondre à des sous-variétés pouvant présenter des singularités: par exemple la fonction δ de Dirac. Une version généralisée aux courants du Théorème de Stokes peut être prouvée..

Soit 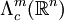$\Lambda_c^m(\mathbb{R}^n)$ la variété différentielle des m-formes à support compact dans Rⁿ. Une application linéaire continue

$T\colon \Lambda_c^m(\mathbb{R}^n)\to \mathbb{R}$

est appelée un m-courant. Soit 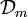$\mathcal D_m$ l'espace des m-courantin Rⁿ. On définit un opérateur de bord

$\partial\colon \mathcal D_{m+1}\to \mathcal D_m$

par

$\partial T(\omega) := T(d\omega).\,$

On peut voir alors que les courants représentent une généralisation des m-surfaces. En effet, si M une variété compacte de dimension m et orientée, on peut lui associer le courant M' défini par

$M(\omega)=\int_M \omega.\,$

Alors, la définition du bord 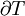$\partial T$ d'un courant, est justifiée par le théorème de Stokes:

$\int_{\partial M} \omega = \int_M d\omega.\,$

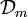L'espace $\mathcal D_m$ des courants à m dimensions est un espace vectoriel réel avec pour opérations:

$(T+S)(\omega):= T(\omega)+S(\omega),\qquad (\lambda T)(\omega):=\lambda T(\omega).$

La somme de 2 courants représente l'union des surfaces correspondantes. La multiplication par un scalaire représentent un changement de la multiplicité de la surface. En particulier, la multiplication par −1 représente un changement d'orientation de a surface.

On définit le support du courant T, noté

$\mathrm{spt}(T),\,$

comme étant le plus petit fermé C tel que

$T(\omega) = 0\,$

si ω = 0 on C.

On note 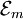$\mathcal E_m$ le sous-espace vectoriel de 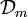$\mathcal D_m$ des courants à supports compacts.

Topologie

L'espace des courants possèdent naturellement une topologie faible induite par celle des formes différentielles. Cela permet alors de définir la notion de convergence faible. On dit qu'une suite T_k converge faiblement vers T si

$T_k(\omega) \to T(\omega),\qquad \forall \omega.\,$

Il existe une norme plus forte sur l'espace des courants qui est la mass norm.

Une norme intermédiaire existe aussi, la flat norm.

A noter que

2 courants sont proches en mass norm s'ils diffèrent d'une petite partie
2 courants sont proches en flat norm s'ils sont égaux à une petite déformation près.

Cas particuliers

On note 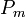$P_m\,$ les courants m-dimensionnel.
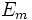$E_m\,$ est l'ensemble des courants à supports compact
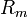$R_m\,$ désigne les courants rectifiables. C'est-à-dire :

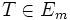$T \in E_m\,$ , tel que les surfaces associées sont de mesure nulle, en comptant les multiplicités.

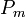$P_m\,$ désigne les chaînes polyhédriques intégrales: c'est le sous-groupe additif de 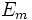$E_m\,$ générés par des simplexes orientés.
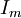$I_m\,$ désigne les courants intégraux:

$I_m = \{ T \in R_m, \partial T \in R_{m-1} \}$

$F_m\,$ désigne les integral flat chains (ou chaînes intégrales plates):*

$F_m = \{ T + \partial S, T \in R_m, S \in R_{m+1} \}$

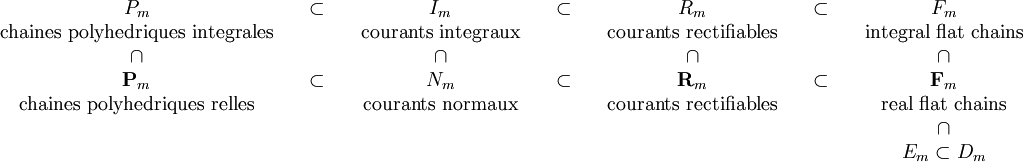
$\left. \begin{array}{ccccccc} P_m & \quad \subset \quad & I_m & \quad \subset \quad & R_m & \quad \subset \quad & F_m \\ \text{chaines polyhedriques integrales} & & \text{courants integraux} & & \text{courants rectifiables} & &\text{integral flat chains} \\ \cap & & \cap & & \cap & & \cap \\ \mathbf{P}_m & \quad \subset \quad & N_m & \quad \subset \quad & \mathbf{R}_m & \quad \subset \quad & \mathbf{F}_m \\ \text{chaines polyhedriques relles} & & \text{courants normaux} & & \text{courants rectifiables} & &\text{real flat chains} \\ & & & & & & \cap \\ & & & & & & E_m \subset D_m \end{array} \right.$

Exemples

On rappelle que

$\Lambda_c^0(\mathbb{R}^n)\equiv C^\infty_c(\mathbb{R}^n)\,$

donc on définit un 0-courant comme:

$T(f) = f(0).\,$

En particulier, toute mesure signée $μ$ avec une masse finie est un 0-courant:

$T(f) = \int f(x)\, d\mu(x).$

Soit (x, y, z) les coordonnées dans R³. Alors, on peut définir un 2-courant comme:

$T(a\,dx\wedge dy + b\,dy\wedge dz + c\,dx\wedge dz) = \int_0^1 \int_0^1 b(x,y,0)\, dx \, dy.$

Bibliographie

PlanetMath
Frank Morgan : Geometric Measure Theory: A Beginner's Guide.
Hassler Whitney : Geometric Integration Theory

Portail des mathématiques

Ce document provient de « Courant (math%C3%A9matiques) ».

Catégories : Analyse fonctionnelle | Topologie différentielle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Courant (Mathématiques) de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

Courant (mathematiques) — Courant (mathématiques) Sommaire 1 Introduction 2 Topologie 3 Cas particuliers 4 Exemples 5 Bibliographie … Wikipédia en Français
Courant (mathématiques) — Sommaire 1 Introduction 2 Topologie 3 Cas particuliers 4 Exemples 5 Bibliographie … Wikipédia en Français
Courant Institute — of Mathematical Sciences Le Courant Institute of Mathematical Sciences (« Institut Courant de sciences mathématiques ») est une division de l Université de New York faisant partie de la faculté des arts et des sciences. L Institut est… … Wikipédia en Français
Courant Institute Of Mathematical Sciences — Le Courant Institute of Mathematical Sciences (« Institut Courant de sciences mathématiques ») est une division de l Université de New York faisant partie de la faculté des arts et des sciences. L Institut est dédié à la recherche et à… … Wikipédia en Français
Courant institute of mathematical sciences — Le Courant Institute of Mathematical Sciences (« Institut Courant de sciences mathématiques ») est une division de l Université de New York faisant partie de la faculté des arts et des sciences. L Institut est dédié à la recherche et à… … Wikipédia en Français
Mathematiques de la relativite generale — Mathématiques de la relativité générale Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils… … Wikipédia en Français
Mathématiques De La Relativité Générale — Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la … Wikipédia en Français
Mathematiques — Mathématiques Les mathématiques constituent un domaine de connaissances abstraites construites à l aide de raisonnements logiques sur des concepts tels que les nombres, les figures, les structures et les transformations. Les mathématiques… … Wikipédia en Français
Mathematiques speciales — Mathématiques spéciales En France, Maths spé ou Mathématiques spéciales est le nom d une ancienne filière de classe préparatoire disparue après la réforme de l enseignement supérieur de 1997, et qui est donné officieusement à une partie des… … Wikipédia en Français
Mathématiques Spéciales — En France, Maths spé ou Mathématiques spéciales est le nom d une ancienne filière de classe préparatoire disparue après la réforme de l enseignement supérieur de 1997, et qui est donné officieusement à une partie des filières de la seconde année… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Courant (Mathématiques)