Mesure bornée
- Mesure bornée
-
Mesure finie
Sur un espace mesurable 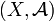 , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.
, une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.
Fonctions intégrables
Toute fonction complexe f mesurable et bornée est intégrable contre toute mesure finie μ ; et on dispose de la majoration :
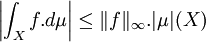
Exemples de mesures finies
- La mesure de comptage sur un ensemble X est finie ssi X est un ensemble fini.
- Les masses de Dirac sont des mesures finies, quel que soit l'espace mesurable considéré.
- Plus généralement, les mesures de probabilité sont des exemples de mesures finies : ce sont des mesures positives de masse 1.
- Pour une mesure complexe ν pas nécessairement finie, et pour une fonction mesurable ν-intégrable, la variation totale de la mesure f.ν est exactement | f | . | ν | ; de fait, la mesure f.ν est finie.
Espace des mesures finies
Toute somme de mesures finies est une mesure finie. Toute mesure proportionnelle à une mesure finie est une mesure finie. Les mesures bornées forment un espace vectoriel complexe 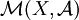 . De plus, on définit la norme :
. De plus, on définit la norme :
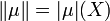
Pour cette norme, c'est un espace de Banach.
Pour toute mesure ν, l'application 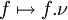 induit une isométrie de
induit une isométrie de 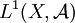 sur un sous-espace vectoriel fermé de
sur un sous-espace vectoriel fermé de 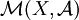 . Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.
. Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie de la mesure
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Mesure bornée de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Mesure Finie — Sur un espace mesurable , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie. Fonctions intégrables Toute fonction complexe f mesurable et bornée… … Wikipédia en Français
Mesure finie — Sur un espace mesurable , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) (en) μ dont la masse | μ | (X) (valeur sur X de la variation |μ| de μ) est finie. Sommaire 1 … Wikipédia en Français
Mesure (mathématiques) — Pour les articles homonymes, voir mesure. Pour une introduction à cette notion, consulter l article : Superficie. En mathématiques, une mesure positive (ou simplement mesure quand il n y a pas de risque de confusion) est une fonction qui… … Wikipédia en Français
Fonction a variation bornee — Fonction à variation bornée En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de… … Wikipédia en Français
Fonction À Variation Bornée — En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de Dirichlet sur la convergence… … Wikipédia en Français
Fonction à variation bornée — En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de Dirichlet sur la convergence… … Wikipédia en Français
INTÉGRATION ET MESURE — La théorie de l’intégration joue en mathématique un rôle extrêmement important. C’est une théorie riche et complexe. Il ne sera pas question ici d’en donner une description exhaustive ni d’en aborder les assez redoutables aspects techniques. On… … Encyclopédie Universelle
Moment (mathématiques) — Pour les articles homonymes, voir Moment. En probabilités (mathématiques, statistiques), on définit le moment d ordre n>0 d une variable aléatoire X, s il existe, le nombre . Sommaire 1 … Wikipédia en Français
fini — fini, ie (fi ni, nie) part. passé de finir. 1° Qui est à sa fin. • Et l on verra peut être avant ce jour fini Ma passion vengée et votre orgueil puni, CORN. Méd. II, 3. • Et ce soir destiné pour la cérémonie Fera voir pleinement si ma haine … Dictionnaire de la Langue Française d'Émile Littré
IMAGINATION — SECTION PREMIÈRE. C est le pouvoir que chaque être sensible sent en soi de se représenter dans son cerveau les choses sensibles. Cette faculté est dépendante de la mémoire. On voit des hommes, des animaux, des jardins: ces perceptions entrent … Dictionnaire philosophique de Voltaire
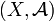 , une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.
, une mesure finie ou mesure bornée est une mesure (réelle ou complexe) μ dont la masse | μ | (X) (valeur de la variation totale | μ | sur X) est finie.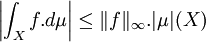
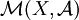 . De plus, on définit la norme :
. De plus, on définit la norme :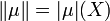
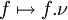 induit une isométrie de
induit une isométrie de 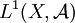 sur un sous-espace vectoriel fermé de
sur un sous-espace vectoriel fermé de 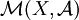 . Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.
. Ce sous-espace est exactement l'ensemble des mesures finies absolument continues par rapport à ν.