Antipodaire
- Antipodaire
-
Podaire
La podaire d'une courbe C par rapport à un point P est le lieu géométrique des projections orthogonales de P sur les tangentes à la courbe C.
Inversément, la courbe C dont une courbe est la podaire s'appelle l'antipodaire (ou podaire inverse).
Étymologie et histoire
La podaire fut étudiée par Maclaurin en 1718 puis par Terquem. Étymologiquement, le terme podaire provient du mot grec podos pied (pied de la perpendiculaire).
Définition mathématique
L'équation paramétrique de la podaire d'une courbe C(t) par rapport à un point P est donnée par :
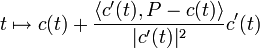
Propriétés et applications
Liens externes
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Antipodaire de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Acceleration de Siacci — Accélération de Siacci En mécanique rationnelle, les composantes de l accélération dans différents systèmes de coordonnées sont bien connues. Dans le cas de courbes planes, on utilise souvent les coordonnées polaires (r, θ). Moins connu, est le… … Wikipédia en Français
Accélération De Siacci — En mécanique rationnelle, les composantes de l accélération dans différents systèmes de coordonnées sont bien connues. Dans le cas de courbes planes, on utilise souvent les coordonnées polaires (r, θ). Moins connu, est le système utilisant la… … Wikipédia en Français
Accélération de Siacci — En mécanique rationnelle, les composantes de l accélération dans différents systèmes de coordonnées sont bien connues. Dans le cas de courbes planes, on utilise souvent les coordonnées polaires (r, θ). Moins connu, est le système utilisant la… … Wikipédia en Français
Accélération de siacci — En mécanique rationnelle, les composantes de l accélération dans différents systèmes de coordonnées sont bien connues. Dans le cas de courbes planes, on utilise souvent les coordonnées polaires (r, θ). Moins connu, est le système utilisant la… … Wikipédia en Français
Constante des aires — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Force centrale, mouvement — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Mouvement a force centrale — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Mouvement À Force Centrale — En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force. Ce type de mouvement est… … Wikipédia en Français
Mouvement à force centrale — En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force. Ce type de mouvement est… … Wikipédia en Français
antipodară — ANTIPODÁRĂ s.f. (mat.) Curbă a cărei podară în raport cu un punct este o curbă dată. [cf. fr. antipodaire]. Trimis de LauraGellner, 13.09.2007. Sursa: DN ANTIPODÁRĂ s. f. (mat.) curbă a cărei podară în raport cu un punct este o curbă dată.… … Dicționar Român