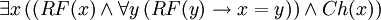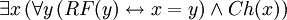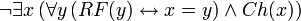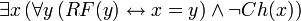Loglangue

La langue de la logique, s'est formée progressivement pour remédier à l'incapacité des langues naturelles à mettre en évidence et à exprimer de façon claire les diverses structures logiques. Des difficultés d'expression analogues ont été rencontrées dans d'autres domaines du savoir, comme la mathématique, la physique, la chimie et même la linguistique. Dans chaque cas, on a dû introduire des notations ou des langues fragmentaires, pour permettre à ces sciences de faire d'immenses progrès. Comme l'écrit Bertrand Russell dans sa préface au Tractatus, «...une bonne notation est si subtile et si suggestive qu'elle en devient parfois semblable à un professeur vivant. Des irrégularités notationnelles sont souvent le premier indice d'erreurs philosophiques et une notation parfaite serait un substitut de la pensée. »^[1]

Sommaire 1 Histoire 2 Points communs avec les langues naturelles 3 Différences entre langue(s)de la logique (ou loglangues) et langues naturelles 4 Exemples 5 Notes 6 Liens externes

Histoire

Il est essentiel de distinguer la logique comme langue de la logique comme déduction ou calcul. Cette distinction, rappelée en 1967 par Van Heijenoort^[2], est déjà présente dès les débuts de la logique. L'oeuvre d'Aristote comprend, en effet, outre une énumération de différentes formes de syllogismes, une ébauche d'élucidation de la structure des propositions. Dès les débuts, la logique possède sa langue. Celle de la logique traditionnelle était toutefois rès limitée en comparaison avec l'actuelle. On s'y tenait à un petit nombre de propositions élémentaires du genre "S est P", "S n'est pas P", "Tout S est P", "Aucun S n'est P", "Quelque S est P", Quelque S n'est pas P", et d'autres construites à partir d'elles avec des connecteurs propositionnels.

Leibniz (1646-1716) est sans doute le premier qui, au travers de sa fameuse caractéristique universelle, conçut le projet d'un vaste formulaire dans lequel on pourrait exprimer toutes les pensées, et pas seulement les notions propres à une discipline particulière. Chez Leibniz apparaît aussi l'idée que formaliser c'est traduire.

Ce projet ne s'est concrétisé que deux siècles plus tard, principalement dans l'idéographie (Begriffsschrift) de Gottlob Frege (1848-1925), mais aussi dans le formulaire de Peano (1858-1932).

Frege assigne comme but à sa Begriffsschrift une formalisation qui est non seulement destinée à vérifier la justesse des raisonnements, mais aussi à fournir une expression adéquate de la diversité des pensées. Il proclame que, à la différence de Boole, sa logique n'est pas simplement un calculus ratiocinator, mais également une lingua characterica au sens de Leibniz.

Les langues frégéennes et péaniennes se sont fortement modifiées depuis. Frege utilisait, par exemple, une écriture bidimensionnelle et sa notation ressemblait davantage à des idéogrammes qu'à l'écriture linéarisée de la loglangue actuelle. On remarquera cependant que des traitements de textes contemporains, comme TeX, ont permis récemment de lui donner un second souffle.

Ces premières langues logiques ont aussi été enrichies de manière à permettre l'analyse de plus en plus subtile à de propositions qui semblaient défier toute formalisation.

C'est cette langue frégéenne, modifiée et enrichie, basée sur le langage des prédicats du premier ordre mais le débordant strictement, par élargissement du cadre extensionnel et intégration de concepts intensionnels, qui constitue la langue de la logique^[3] actuelle.

Quand la langue de logique du premier ordre et de ses extensions est traitée de cette façon comme une langue étrangère, la formalisation, l'interprétation ou la représentation de phrases de la langue naturelle ne sont rien d'autre que des traductions dans ce nouveau langage. Comme dans les autres cas de traduction, on peut procéder de manière intuitive ou de façon automatique, comme chez Montague ou dans la "discourse representation theory" de Kamp^[4].

Points communs avec les langues naturelles

Tout comme le français, la langue de la logique a sa grammaire propre. Celle-ci comprend un ensemble de lettres, qui forment son alphabet et qui permettent de construire des expressions grammaticalement correctes.

Les lettres ou symboles sont groupés en sortes:

• les symboles propositionnels, prédicatifs et fonctionnels ;
• les constantes ;
• les variables, qui, comme les constantes, peuvent être de différents types ;
• les symboles logiques, pouvant inclure des opérateurs non extensionnels (modaux, temporels, implications relevantes etc.);
• les signes de ponctuation, comme les parenthèses.

Toute suite finie de lettres de l'alphabet est une expression. Mais toute expression n'est pas grammaticale. Comme en français ---où on distingue les catégories de noms, verbes, prépositions et adjectifs--- les expressions grammaticales sont tépartis en différentes catégories:

• les termes, construits avec les symboles fonctionnels, les variables et les constantes ---la définition des termes évoque la morphologie d'une langue naturelle;

• les énoncés simples et complexes ---les règles de formation des énoncés correspondent à la syntaxe d'une langue naturelle.

Tout comme une langue naturelle, la langue de la logique est vivante, en ce sens qu'elle évolue en s'adjoignant de nouveaux mots et en se débarrassant d'expressions désuètes et d'archaïsmes. Elle possède aussi de nombreux dialectes et de systèmes d'écriture. C'est pourquoi, il est plus exact de parler d'en parler au pluriel : les langues propositionnelle, prédicative, modale, à plusieurs types d'objets ...

Différences entre langue(s)de la logique (ou loglangues) et langues naturelles

• La grammaire d'une loglangue est précise et complète. Dans le cadre d'une loglangue déterminée, la frontière qui sépare les expressions grammaticalement correctes et les autres est nette. Une loglangue est en principe entièrement décrite par une unique grammaire, constitutive de la langue. Les langues naturelles en revanche n'ont pas de grammaire unique; leurs grammaires généralement incomplètes sont des théories a posteriori visant à décrire plus ou moins fidèlement la structure de la langue.
• Les loglangues sont avant tout écrites. Les énoncés oraux occasionnels font toujours référence à des expressions écrites ou susceptibles de l'être.
• Une loglangue n'a pas vocation à être une langue maternelle, ni même une langue naturelle, comme l'esperanto, voire un idiome comme loglan, qui est plus une "langue logique"^[5] qu'une langue de la logique. Ce qui n'implique pas qu'on assigne a priori des limites à son pouvoir d'espression.

Exemples

Avec les êtres humains, comme univers de discours, et un symbole binaire A signifiant ...aime....

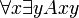= Tout le monde aime quelqu'un.

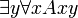= Quelqu'un est aimé par tout le monde.

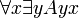= Tout le monde est aimé (de quelqu'un).

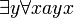= Il y a quelqu'un qui aime tout le monde.

Voici deux traductions en loglangue du fameux exemple de la théorie des descriptions de Russell, L'actuel roi de France est chauve.

• 
• 

Ces traductions sont équivalentes. Par contre, les traductions suivantes de L'actuel roi de France n'est pas chauve ne le sont pas, la première étant vraie et la seconde fausse,

• 
• 

Notes

Liens externes

• Un cours de loglangue.
• (en) Indications pour la traduction, par Peter Suber.
• "Logical Form", Paul Pietroski, Stanford Encyclopedia of Philosophy

• Portail de la philosophie
• Portail de la linguistique
• Portail de la logique