Identite de MacWilliams

Identite de MacWilliams

Identité de MacWilliams

En mathématiques l'identité de MacWilliams est une application de l'analyse harmonique sur un groupe abélien fini, dans le cas où le groupe est un espace vectoriel de dimension finie sur un corps fini.

Elle est utilisée essentiellement en théorie des codes, pour les codes linéaires, elle relie les polynômes énumérateurs des poids d'un code et de son dual, permettant ainsi, par exemple, de déterminer le polynôme énumérateur des poids du dual à partir de celui du code.

Sommaire

Position du problème

Objectif

Article détaillé : Code linéaire.

Dans cet article C désigne un code de paramètre [n, k, δ] sur le corps fini Fd où d est un entier puissance d'un nombre premier p.

L'objectif de l'identité de MacWilliams est de répondre à la question suivante : soit C un code linéaire quel est la distance minimale au sens de Hamming de son code dual ?

La réponse de dépend pas uniquement de la distance minimale de C, il est en fait nécessaire de connaître toute la distribution des poids du code C, ce qui donne lieu à la définition suivante :

  • Le polynôme énumérateur des poids est le polynôme dont à coefficients à valeur dans les entiers positifs tel que si i est un entier positif le coefficient du monôme Xi est égal au nombre de mots du code de poids de Hamming égal à i.

Le polynôme énumérateur des poids correspond donc à la distribution des différents poids du code.

Considérons par exemple le cas où n est égal à k, c'est-à-dire celui où il n'existe aucune redondance, la sphère de rayon i et de centre le vecteur nulle contient exactement ai points avec :

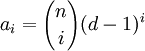
a_i= {n \choose i} (d-1)^i \;

C'est-à-dire le i-ème coefficient binomial d'ordre n que multiplie le nombre de lettres différente de 0 de l'alphabet à la puissance i. Dans ce cas, le polynôme énumérateur P[X] est égal à :

P[X]= \sum_{i=0}^n a_i X^i = \sum_{i=0}^n {n \choose i} (d-1)^i X^i= \Big(1 + (d-1)X \Big)^n \;

L'objectif est de trouver le polynôme énumérateur des poids du code dual, dans l'exemple le code dual ne contient qu'un unique mot, le mot nul, sont polynôme énumérateur est donc le polynôme nul.

Outils

Article détaillé : Analyse harmonique sur un espace vectoriel fini.

L'espace vectoriel utilisé ici, à savoir Fdn, est un groupe abélien fini pour l'addition, son groupe dual est donc fini et isomorphe à (Fdn +), la théorie de l'analyse harmonique est relativement simple. Dans ce contexte, elle permet de définir une transformée de Fourier disposant des propriétés usuelles comme l'égalité de Parseval ou la formule sommatoire de Poisson.

La théorie est encore simplifiée du fait de la structure d'espace vectoriel du groupe, il existe un isomorphisme entre le groupe et son espace dual. Si μ est un caractère non trivial sur le groupe additif du corps Fd, tous les caractères s'écrivent sous la forme χy suivante :

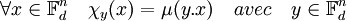
\forall x \in \mathbb F_d^n \quad \chi_y(x) = \mu (y.x) \quad avec \quad y \in \mathbb F_d^n\;

Ici . désigne la forme bilinéaire non dégénérée définie par l'égalité suivante, si x = (xi) et y = (yi) désigne deux vecteurs de Fdn :

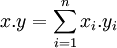
x.y = \sum_{i=1}^n x_i.y_i\;

Identité de MacWilliams

Avec les notations du paragraphe précédent, si Q[X] désigne le polynôme énumérateur des poids du code dual de C, alors l'égalité suivante est vérifiée :

Q[X]=\frac 1{d^k}\Big( 1 + (d-1)X\Big)^n P\Big(\frac{1-X}{1 + (d-1)X} \Big)\;


Démonstration

Considérons la fonction g de Fdn dans C[X] l'anneau des polynômes à coefficients complexes, définie par :

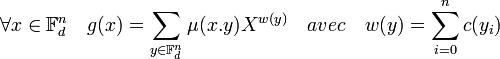
\forall x \in \mathbb F_d^n \quad g(x) = \sum_{y \in \mathbb F_d^n}\mu(x.y) X^{w(y)} \quad avec \quad w(y) = \sum_{i = 0}^n c(y_i) \;

Ici c désigne la fonction de Fd dans C qui à 0 associe 0 et à tout autre élément associe 1. L'application w correspond donc à la fonction poids de Hamming. Une fois encore, (yi) désigne les différentes coordonnées de y dans la base canonique de Fdn.

  • Le polynôme Q[X], défini par l'égalité suivante, est le polynôme énumérateur des poids du code dual de C.
Q[X] = \frac 1{q^k} \sum_{c \in C} g(c) \;

La définition du polynôme Q[X] montre que :

Q[X] = \frac 1{q^k} \sum_{c \in C} g(c) = \frac 1{q^k} \sum_{y \in \mathbb F_d^n} \sum_{c \in C} \mu(c.y) X^{w(y)} = \frac 1{q^k} \sum_{y \in \mathbb F_d^n} b_y X^{w(y)} \quad avec \quad b_y = \sum_{c \in C} \mu(c.y) \;

Il est donc nécessaire de calculer by. Si y est un élément du code dual, alors c.y est égal à 0 pour tout c élément de C, on en déduit que μ(c.y) est égal à 1 et by est égal au cardinal de C, c'est-à-dire qk. Si y n'est pas élément de C, alors l'application qui à c associe μ(c.y) est un caractère non trivial du groupe (C, + ). Il est donc orthogonal au caractère trivial, cette relation d'orthogonalité exprime le fait que by est nul. On en déduit que :

Q[X]=\sum_{c \in C^{\perp}} X^{w(c)} \;

Cette dernière égalité démontre que Q[X] est bien le polynôme annulateur du code dual.

  • le polynôme Q[X] vérifie l'égalité suivante :
Q[X]=\frac 1{d^k}\Big( 1 + (d-1)X\Big)^n P\Big(\frac{1-X}{1 + (d-1)X} \Big)\;

Si (ci) sont les coordonnées de c et (yi) celle de y, alors les égalités suivantes sont vérifiées :

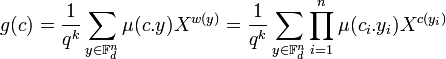
g(c) = \frac 1{q^k} \sum_{y \in \mathbb F_d^n}\mu(c.y) X^{w(y)} = \frac 1{q^k} \sum_{y \in \mathbb F_d^n} \prod_{i=1}^n \mu(c_i.y_i) X^{c(y_i)} \;

Calculons alors la valeur suivante :

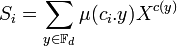
S_i = \sum_{y \in \mathbb F_d} \mu(c_i.y) X^{c(y)} \;

Si ci est nul alors μ(ci.y) est égal à 1 pour toute valeur de y, c(y) vaut 0 si y est nul et 1 sinon, on en déduit que Si = 1 + (q - 1)X. Si ci est non nul alors l'application qui à y associe μ(ci.y) est un caractère non trivial du groupe additif du corps Fd. Il est donc orthogonal au caractère trivial et :

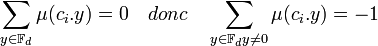
\sum_{y \in \mathbb F_d} \mu(c_i.y) = 0 \quad donc \quad \sum_{y \in \mathbb F_d y \ne 0} \mu(c_i.y) = -1 \;

On en déduit les égalités suivantes :

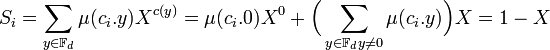
S_i = \sum_{y \in \mathbb F_d} \mu(c_i.y) X^{c(y)} =\mu(c_i.0)X^0 + \Big(\sum_{y \in \mathbb F_d y \ne 0} \mu(c_i.y) \Big)X = 1 -X \;

On en déduit l'égalité suivante :

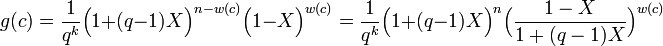
g(c) = \frac 1{q^k}\Big(1 + (q-1)X \Big)^{n-w(c)}\Big( 1 -X \Big)^{w(c)}=\frac 1{q^k}\Big(1 + (q-1)X \Big)^n \Big(\frac {1-X}{1 + (q-1)X} \Big)^{w(c)}\;

On obtient donc pour expression de Q[X], l'égalité suivante :

Q[X] = \frac 1{q^k}\Big(1 + (q-1)X \Big)^n \sum_{c \in C} \Big(\frac {1-X}{1 + (q-1)X} \Big)^{w(c)}= \frac 1{d^k}\Big( 1 + (d-1)X\Big)^n P\Big(\frac{1-X}{1 + (d-1)X} \Big)\;

Ce qui termine la démonstration.

Applications

Code sans redondance

Considérons le code sans redondance de l'exemple du paragraphe des objectifs, le polynôme énumérateur des poids du code est :

P[X]= \Big(1 + (d-1)X \Big)^n \;

L'identité de MacWilliams donne pour valeur de Q[X] polynôme énumérateur du code dual :

Q[X]=\frac 1{d^n}\Big( 1 + (d-1)X\Big)^n \Big( 1 + (d-1)\frac{1-X}{1 + (d-1)X} \Big)^n \;

Ce qui donne les égalités suivantes :

Q[X]=\frac 1{d^n}\Big( 1 + (d-1)X\Big)^n \Big(\frac{d}{1 + (d-1)X} \Big)^n = 1 \;

Le code dual possède en effet un unique élément de poids nul, l'identité de MacWilliams fournit bien le polynôme énumérateur du code dual.

Code de Hamming

Article détaillé : Code de Hamming.

Déterminons le polynôme énumérateur des poids du code de Hamming. La méthode utilisée ici consiste à déterminer le polynôme énumérateur du code dual directement et d'utiliser l'identité de MacWilliams pour déterminer le polynôme énumérateur du code dual du code dual, égal au code de Hamming.

Les notations utilisées ici sont celles de l'article détaillé, en particulier m désigne la valeur n - k, c'est-à-dire la dimension du code dual et H désigne la matrice de contrôle du code.

  • Tous les mots du code dual non nuls du code de Hamming ont un poids égal à dm-1.

En effet, le code dual est constitué des mots de la forme tx.H où x décrit l'espace vectoriel Fdm. Désignons par (hi) pour i variant de 1 à n les n colonnes de la matrice H qui sont aussi des vecteurs de dimension m. L'application qui à x associe le vecteur (x.hi) est donc un isomorphisme entre Fdm et le code dual.

Soit A l'ensemble des vecteurs a de Fdm tel que a.x soit différent de 0. L'intersection des classes de l'espace projectifs avec A forment une partition de A. De plus, a.x est différent de 0 si et seulement si λa.x est différent de 0 pour tout λ élément de Fd*. En conséquence chaque classe de la partition de A contient d - 1 éléments. Enfin, les vecteurs hi décrivent un système de représentants des classes de l'espace projectif de Fdm (cf le paragraphe Existence et unicité dans le cas général). On en déduit que le poids de (x.hi) est égal à la fraction de numérateur le cardinal de A et de dénominateur d - 1.

Le complémentaire de A, si x n'est pas nul, est un hyperplan de Fdm donc un ensemble de cardinal dm - 1. Le cardinal de A est donc égal à dm - 1. (d - 1). Le poids de (x.hi) est alors égal à dm - 1 si x n'est pas nul.

  • Le polynôme énumérateur des poids du code de Hamming P[X] est défini par l'égalité suivante :
P[X]=\frac 1{d^m}\Bigg( \Big( 1 + (d-1)X\Big)^n + (d^m -1)\Big( 1 + (d-1)X\Big)^{n-d^{m-1}}(1 - X)^{d^{m-1}} \Bigg)\;

En effet, le polynôme énumérateur des poids du code dual est le suivant :

Q[X]=1 + (d^m -1)X^{d^{m-1}}\;

L'identité de MacWilliams montre alors que :

P[X]=\frac 1{d^m}\Big( 1 + (d-1)X\Big)^n \Big( 1 + (d^m -1)\Big( \frac{1-X}{1 + (d-1)X} \Big)^{d^{m-1}}\Big) = \frac 1{d^m}\Bigg( \Big( 1 + (d-1)X\Big)^n + (d^m -1)\Big( 1 + (d-1)X\Big)^{n-d^{m-1}}(1 - X)^{d^{m-1}} \Bigg)\;

Ce qui termine la démonstration.


Notes et références

Voir aussi

Articles connexes

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Bibliographie

  • M. Demazure Cours d'algèbre. Primalité, divisibilité, codes Cassini 1997
  • F. J. MacWilliams & NJA Sloane The Theory of Error-Correcting Codes North-Holland, 1977
  • A. Warusfel Structures algébriques finies Hachette 1971
  • G. Peyré L'algèbre discrète de la transformée de Fourier Ellipses Marketing 2004

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Identit%C3%A9 de MacWilliams ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Identite de MacWilliams de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Identité de MacWilliams — En mathématiques, l identité de MacWilliams est une application de l analyse harmonique sur un groupe abélien fini, dans le cas où le groupe est un espace vectoriel de dimension finie sur un corps fini. Elle est utilisée essentiellement en… …   Wikipédia en Français

  • Identité De Mac Williams — Identité de MacWilliams En mathématiques l identité de MacWilliams est une application de l analyse harmonique sur un groupe abélien fini, dans le cas où le groupe est un espace vectoriel de dimension finie sur un corps fini. Elle est utilisée… …   Wikipédia en Français

  • Identité de Mac Williams — Identité de MacWilliams En mathématiques l identité de MacWilliams est une application de l analyse harmonique sur un groupe abélien fini, dans le cas où le groupe est un espace vectoriel de dimension finie sur un corps fini. Elle est utilisée… …   Wikipédia en Français

  • Identité de mac williams — Identité de MacWilliams En mathématiques l identité de MacWilliams est une application de l analyse harmonique sur un groupe abélien fini, dans le cas où le groupe est un espace vectoriel de dimension finie sur un corps fini. Elle est utilisée… …   Wikipédia en Français

  • Arithmétique modulaire — Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes… …   Wikipédia en Français

  • Analyse harmonique sur un espace vectoriel fini — En mathématiques et plus précisément dans le cadre de la théorie de l analyse harmonique, l analyse harmonique sur un espace vectoriel fini correspond au cas particulier où le groupe est le groupe additif d un espace vectoriel fini. Ce contexte s …   Wikipédia en Français

  • Analyse Harmonique Sur Un Espace Vectoriel Fini — En mathématiques et plus précisément dans le cadre de la théorie de l analyse harmonique, l analyse harmonique sur un espace vectoriel fini correspond au cas particulier où le groupe est le groupe additif d un espace vectoriel fini. Ce contexte s …   Wikipédia en Français

  • Code linéaire — En mathématiques, plus précisément en théorie des codes, un code linéaire est un code correcteur. Il est structuré comme un sous espace vectoriel d un espace vectoriel de dimension finie sur un corps fini. L espace vectoriel fini utilisé est… …   Wikipédia en Français

  • Code Linéaire — En mathématiques, plus précisément en théorie des codes, un code linéaire est un code correcteur. Il est structuré comme un sous espace vectoriel sur un corps fini. L espace utilisé est souvent F2n le terme usuel est alors celui de code linéaire… …   Wikipédia en Français

  • Code lineaire — Code linéaire En mathématiques, plus précisément en théorie des codes, un code linéaire est un code correcteur. Il est structuré comme un sous espace vectoriel sur un corps fini. L espace utilisé est souvent F2n le terme usuel est alors celui de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”