- Isomorphisme de graphes
-
Morphisme de graphes
Un morphisme de graphe ou homomorphisme de graphe est une application entre deux graphes qui respecte la structure de ces graphes. Autrement dit l'image d'un graphe G dans un graphe H doit respecter les relations d'adjacence présentes dans G.
Sommaire
Formalisation
Si G et H sont deux graphes, une application
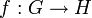est un morphisme de graphe si f = (fV,fE), où 
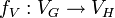, transforme les sommets de G en ceux de H et si 
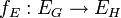transforme les arêtes de G en celles de H en respectant la contrainte suivante : s'il existe une arête 
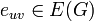entre deux sommets de G, alors il doit y avoir une arête 
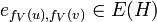entre les deux sommets correspondants de H.Notation et cardinalités
La notation[1] HOM(G,H) dénote l'ensemble des homomorphismes
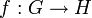et hom(G,H) est le nombre de tels homomorphismes, c'est-à-dire la cardinalité de HOM(G,H). On dit de l'homomorphisme f qu'il est une injection (respectivement surjection) si ses deux fonctions fV et fE sont injectives (respectivement surjectives); si elles sont à la fois injectives et surjectives, c'est-à-dire bijectives, alors f est un isomorphisme. On utilise les notations INJ(G,H) pour l'injection, SUR(G,H) pour la surjection et BIJ(G,H) pour la bijection.L'isomorphisme peut aussi s'exprimer de la façon suivante : les graphes ont le même nombre de sommets, c'est-à-dire V(G) = V(H), et sont connectés de la même façon. Autrement dit, si les deux graphes venaient à être dessinés, alors il n'y aurait qu'à déplacer les sommets de l'un pour obtenir la copie conforme de l'autre, comme cela est illustré ci-dessous.
Cette notion nous permet d'introduire celle de l'étiquetage : à chaque sommet est associé une étiquette, souvent un entier allant de 1 à V(G) = n mais il peut s'agir d'un alphabet quelconque permettant ainsi à l'étiquette d'un sommet de contenir des renseignements sur sa localisation (qui pourront ensuite être utilisés pour des problèmes de routage). Si on s'intéresse aux graphes étiquetés, alors il suffit que les étiquettes de certains sommets soient différents pour que l'on considère les graphes différents; cependant, les graphes peuvent être équivalents au niveau de la structure et on dira qu'ils sont isomorphes.
Graphe G Graphe H Isomorphisme
entre G et H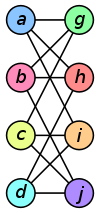
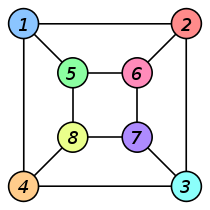
ƒ(a) = 1 ƒ(b) = 6
ƒ(c) = 8
ƒ(d) = 3
ƒ(g) = 5
ƒ(h) = 2
ƒ(i) = 4
ƒ(j) = 7
Problème du chemin
Une propriété de l'homomorphisme découlant directement de la définition concerne l'existence d'un chemin : la contrainte sur la structure impose à toute arrête du graphe d'origine d'exister dans l'image.
Si l'on se trouve sur le sommet v0 et que l'on va à v1 par l'arête
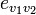, alors on pourra faire le même chemin dans l'image par l'arrête 
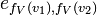; on obtient par induction que tout chemin de G se retrouve par le chemin des images dans H.Extensions et variantes
Une extension au problème a été proposée en 2006[2] : en associant un sommet
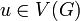à un sommet i de H, on paye un coût que l'on note 
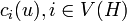, et l'on peut alors définir le coût d'un homomorphisme par l'ensemble du coût donné par chaque association de fV soit :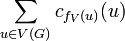
Le but est de déterminer s'il existe un homomorphisme dont le coût ne dépasse pas une limite k.
Parmi les autres variantes du problème, on peut spécifier pour chaque sommet une liste d'images permises[3].
Notes et références
- ↑ (en) Pavol Hell et Jaroslav Nesetril : Graphs and Homomorphisms. Oxford University Press, 2004. (ISBN 0198528175)
- ↑ (en) Gregory Gutin et Arash Rafiey et A. Yeo : Level of repair analysis and minimum cost homomorphisms of graphs. Discrete Applied Math., volume 154, pages 890–897, 2006.
- ↑ (en) Pavol Hell : Algorithmic aspects of graph homomorphisms. Survey in Combinatorics, London Math. Society, Cambridge University Press, pages 239–276, 2003.
Portail des mathématiques
Catégories : Théorie des catégories | Théorie algébrique des graphes
Wikimedia Foundation. 2010.
