Inégalité de korn
- Inégalité de korn
-
Inégalité de Korn
Énoncé
Soit 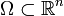 un ouvert borné dont la frontière est suffisamment régulière (par exemple
un ouvert borné dont la frontière est suffisamment régulière (par exemple 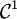 par morceau). Notons
par morceau). Notons  le linéarisé du tenseur des contraintes défini pour tout
le linéarisé du tenseur des contraintes défini pour tout 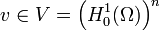 par
par
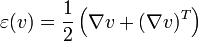 .
.
Alors il existe c > 0 telle que
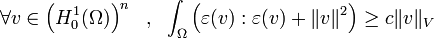
En notation indicielle avec 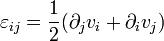 cette inéquation s'écrit
cette inéquation s'écrit
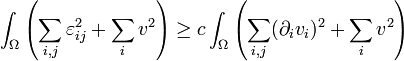 .
.
Bibiographie
- Duvaut G. Lions J.L., Les inéquations en mécanique et en physique, Dunod (1972)
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inégalité de korn de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Inégalité de Korn — Énoncé Soit un ouvert borné dont la frontière est suffisamment régulière (par exemple par morceau). Notons ε le linéarisé du tenseur des déformations défini pour tout par . Alors il existe c > … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Killing Joke — Cet article concerne le groupe de musique. Pour l album homonyme sorti en 1980, voir Killing Joke (album). Pour celui de 2003, voir Killing Joke (album, 2003). Killing Joke … Wikipédia en Français
 un ouvert borné dont la frontière est suffisamment régulière (par exemple
un ouvert borné dont la frontière est suffisamment régulière (par exemple 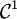 par morceau). Notons
par morceau). Notons  le linéarisé du tenseur des contraintes défini pour tout
le linéarisé du tenseur des contraintes défini pour tout 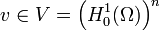 par
par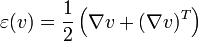 .
.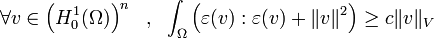
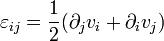 cette inéquation s'écrit
cette inéquation s'écrit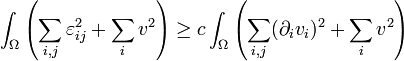 .
.