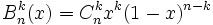Interpolation de Berstein

L'approximation de Bernstein est une méthode d'approximation polynomiale permettant d'approcher uniformément une fonction continue définie sur l'intervalle par une famille de polynômes, appelés polynômes de Bernstein. Cela donne une version constructive du théorème de Stone-Weierstrass.

Ces polynômes sont de la forme

pour un entier , où 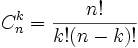est le coefficient binomial, c'est-à-dire le nombre de combinaisons d'un ensemble de k éléments (sans les distinguer) parmi . On construit donc une approximation de par la fonction

.

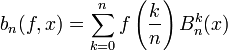On construit 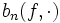à partir des valeurs de f aux points 0,1 / n,...,1 mais, en ces points, la valeur de 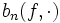peut être différente de celle de f. Selon certaines définitions, cela en fait un procédé d'interpolation ou non.

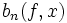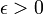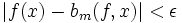La convergence uniforme de vers s'énonce donc de la façon suivante : pour tout , il existe un entier assez grand tel que pour tout et tout entier .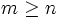

Il convient de noter que si 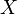est une variable aléatoire suivant une loi binomiale de paramètres 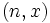, alors 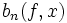n'est rien d'autre que l'espérance de 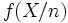, c'est-à-dire la moyenne de appliquée au nombre de succès de n expériences indépendantes de probabilité . Le convergence ponctuelle de 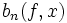(c'est-à-dire pour chaque point ) vers 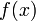est alors une conséquence immédiate de la loi faible des grands nombres. 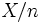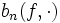En majorant la probabilité de l'écart entre et , on en déduit facilement la convergence uniforme de vers

Référence

• S. Bernstein, Démonstration du théorème de Weierstrass, fondée sur le calcul des probabilités. Charkow Ges. (2) 13, 1-2, 1912.

• Portail des mathématiques