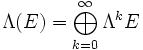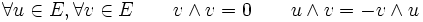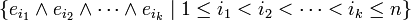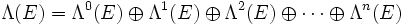Algèbre de Grassmann

Algèbre de Grassmann

Algèbre extérieure

Hermann Grassmann, date inconnue.

En algèbre et en analyse vectorielle, l'algèbre extérieure d'un espace vectoriel E est une algèbre graduée, notée Λ * E. Une présentation informelle de cette algèbre est donnée dans la première partie ci-dessous.

Pour simplement comprendre les notations : * désigne ici la graduation. Elle est entière et commence par 0. L'ensemble ΛkE est un espace vectoriel sur le corps K. Ses éléments sont exactement ceux de degré k. Au moins en géométrie, ils sont souvent appelés des k-multivecteurs, ou plus simplement bivecteurs pour k=2. En particulier, Λ0E = K et Λ1E = E. L'espace vectoriel Λ * E est la somme directe des ΛkE où k décrit N. Sa loi multiplicative, appelée le produit extérieur, est notée par le symbole wedge \wedge. Elle est associative, bilinéaire et alternée. On dit qu'elle est "anti-commutative" ou "commutative au sens graduée" (voir plus bas).

L'algèbre extérieure est aussi appelée algèbre de Grassmann nommée ainsi en l'honneur de Hermann Grassmann. Vers 1840, ce dernier a écrit un traité sur les "grandeurs extensives", précurseurs des multivecteurs.

L'algèbre extérieure est particulièrement utile en topologie algébrique élémentaire et surtout en géométrie différentielle et en physique mathématique. Elle permet en particulier de définir les formes différentielles et les champs de multivecteurs. En géométrie algébrique, l'algèbre extérieure intervient dans l'étude des faisceaux localement libres. Ces applications sont à peine abordées dans cet article qui se veut avant tout introductif.

Une première approche

L'algèbre extérieure peut être caractérisée comme l'algèbre la « plus simple » possédant les propriétés précédentes, ce qui s'exprime formellement à l'aide d'un problème universel. Dans un premier temps on peut se contenter d'une description par générateurs et relations.

Les éléments de la forme 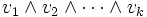v_1\wedge v_2\wedge\cdots\wedge v_k avec v1, …, vk dans E sont appelés k-vecteurs. Le sous-espace de Λ(E) engendré par tous les k-vecteurs porte le nom de k-ème puissance extérieure de E et se note Λk(E). Les éléments de cet espace sont donc des combinaisons de k-vecteurs, pas forcément des k-vecteurs.

L'algèbre extérieure apparaît comme la somme directe des puissances extérieures successives :

\Lambda(E) = \bigoplus_{k=0}^{\infty} \Lambda^k E

L'indice k forme un degré compatible avec le produit extérieur : le produit d'un k-vecteur et d'un l-vecteur est un vecteur de degré inférieur à k+l. Ainsi l'algèbre extérieure a une structure d'algèbre graduée.

Les relations

\forall u \in E, \forall v \in E \qquad v\wedge v = 0 \qquad u\wedge v = - v\wedge u

ne sont vraies en général que pour des vecteurs, pas pour des k-vecteurs, ni des éléments de l'algèbre extérieure.

Une interprétation géométrique des k-vecteurs : le 2-vecteur 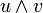u\wedge v représente le parallélogramme orienté de côtés u et v, le 3-vecteur 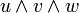u\wedge v\wedge w représente le parallélépipède orienté de côtés u, v, et w.

Base et dimension

Si E est de dimension n et de base (e1, ..., en), alors il est possible de donner une base de la k-ème puissance extérieure Λk(E), sous la forme

\{e_{i_1}\wedge e_{i_2}\wedge\cdots\wedge e_{i_k} \mid 1\le i_1 < i_2 < \cdots < i_k \le n\}

En effet, c'est un résultat général de décomposition pour les applications multilinéaires alternées. Chacune des composantes du k-vecteur sur cette base est un mineur de la matrice représentative du système de vecteurs vj sur la base ei.

La dimension de Λk(E) est le coefficient binomial 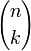{n \choose k}. Notamment, Λk(E) = {0} pour k > n.

L'algèbre extérieure est une algèbre graduée égale à la somme directe

\Lambda(E) = \Lambda^0(E)\oplus \Lambda^1(E) \oplus \Lambda^2(E) \oplus \cdots \oplus \Lambda^n(E)

(dans laquelle Λ0(E) = K et Λ1(E) = E), et sa dimension est donc 2n.

Définitions formelles

L'algèbre Λ * E est l'algèbre graduée la plus générale contenant E, avec un produit ayant la propriété d'alternance. Il est naturel de voir dans ce problème une variante de l'introduction de l'algèbre tensorielle T(E), et d'obtenir la propriété d'alternance par un quotient adapté. Soit donc I l'idéal bilatère de T(E) engendré par les éléments de la forme 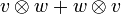v \otimes w+w\otimes v pour v et w appartenant à E. L'espace 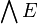\bigwedge E est défini comme le quotient

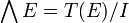\bigwedge E = T(E)/I.



  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Alg%C3%A8bre ext%C3%A9rieure ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algèbre de Grassmann de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Algebre exterieure — Algèbre extérieure Hermann Grassmann, date inconnue. En algèbre et en analyse vectorielle, l algèbre extérieure d un espace vectoriel E est une algèbre graduée, notée Λ * E. Une présentation informelle de cette algèbre est donnée dans la première …   Wikipédia en Français

  • Algèbre Extérieure — Hermann Grassmann, date inconnue. En algèbre et en analyse vectorielle, l algèbre extérieure d un espace vectoriel E est une algèbre graduée, notée Λ * E. Une présentation informelle de cette algèbre est donnée dans la première partie ci dessous …   Wikipédia en Français

  • Algebre multilineaire — Algèbre multilinéaire En mathématiques, l’algèbre multilinéaire étend les méthodes de l’algèbre linéaire. Tout comme l’algèbre linéaire est bâtie sur le concept d’un vecteur et développe la théorie des espaces vectoriels, l’algèbre multilinéaire… …   Wikipédia en Français

  • Algèbre Multilinéaire — En mathématiques, l’algèbre multilinéaire étend les méthodes de l’algèbre linéaire. Tout comme l’algèbre linéaire est bâtie sur le concept d’un vecteur et développe la théorie des espaces vectoriels, l’algèbre multilinéaire est bâtie sur le… …   Wikipédia en Français

  • Algèbre extérieure — Pour les articles homonymes, voir Algèbre (homonymie). Hermann Grassmann, date inconnue. En mathématiques, et plus précisément en algèbre et en analyse vectorielle …   Wikipédia en Français

  • Grassmann — Hermann Günther Grassmann Hermann Günther Grassmann Hermann Günther Grassmann (15 avril 1809 à Stettin 26 septembre 1877 à Stettin) était un polymathe allemand. À son époque, il était connu en tant que …   Wikipédia en Français

  • Algèbre multilinéaire — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, l’algèbre multilinéaire étend les méthodes de l’algèbre linéaire. Tout comme l’algèbre linéaire est bâtie sur le concept de vecteur et développe la théorie des espaces… …   Wikipédia en Français

  • Algèbre (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot « algèbre » vient de l arabe ’al ǧabr (« réduction »), désignant une technique de chirurgie des membres puis une technique de… …   Wikipédia en Français

  • ALGÈBRE — L’algèbre au sens moderne, à savoir l’étude des structures algébriques indépendamment de leurs réalisations concrètes, ne s’est dégagée que très progressivement au cours du XIXe siècle, en liaison avec le mouvement général d’axiomatisation de… …   Encyclopédie Universelle

  • GRASSMANN (H. G.) — GRASSMANN HERMANN GÜNTHER (1809 1877) Mathématicien et philosophe allemand, né et mort à Stettin (aujourd’hui Szczecin). Fils d’un pasteur protestant, Hermann Grassmann étudia d’abord la théologie à Berlin avant d’enseigner les mathématiques,… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”