- Identités Logarithmiques
-
Identités logarithmiques
Voici une liste d'identités utiles lorsqu'on travaille avec les logarithmes. Toutes sont valables à condition que les réels utilisés (a, b, c et d) soient strictement positifs. En outre, les bases des logarithmes doivent être différentes de 1.
Sommaire
Valeurs particulières
Multiplication, division et exponentiation
Ces trois identités nous permettent d'utiliser des tables de logarithme et des règles à calcul ; connaissant le logarithme de deux nombres, nous pouvons les multiplier et diviser rapidement, ou aussi bien calculer des puissances ou des racines de ceux-ci.
Formules de G. G. Gendre:
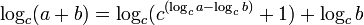 pour a > b
pour a > b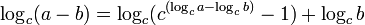 pour a > b
pour a > b
Ces formules permettent dans certains cas de calculer numériquement log(a + b) en fonction de log(a) et log(b) en évitant des dépassements des limites numériques.
Réciprocité
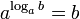
- pour tout nombre réel r, loga(ar) = r
Les formules précédentes sont utilisées pour résoudre des équations dont les inconnues sont en exposant.
Changement de base
Cette identité est utile pour calculer des logarithmes avec des machines à calculer, car la plupart des ces dernières ne proposent que les logarithmes décimaux et naturels.
DémonstrationCette formule découle simplement du rapport constant lors du changement de base.
Hypothèse :
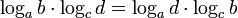
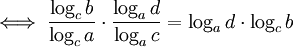 (changement de base à gauche)
(changement de base à gauche)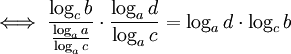 (changement de base de logca)
(changement de base de logca)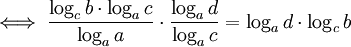 (multiplication par l'inverse)
(multiplication par l'inverse)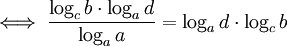 (simplification des logac)
(simplification des logac)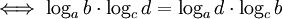 (simplification de logaa)
(simplification de logaa)
∎CQFD
Limites
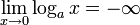 pour a > 1
pour a > 1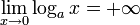 pour 0 < a < 1
pour 0 < a < 1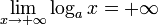 pour a > 1
pour a > 1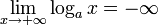 pour 0 < a < 1
pour 0 < a < 1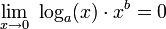 pour b rationnel positif
pour b rationnel positif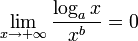 pour b rationnel positif
pour b rationnel positif
La dernière limite est souvent interprétée comme « en l'infini le logarithme croît plus lentement que toute puissance (strictement positive) de la variable ».
Dérivée
Dans le cas particulier de la base e :
Primitive
- Portail des mathématiques
Catégories : Analyse réelle | Identité mathématique | Logarithme
Wikimedia Foundation. 2010.

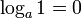
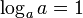
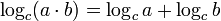
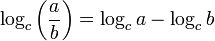
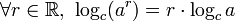
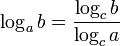
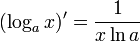
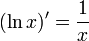
![\int\log_ax\;\mathrm dx = x\cdot\left[\log_ax-\frac{1}{\ln a}\right]](/pictures/frwiki/55/763d703937785d372a0a5dadcbacd033.png)