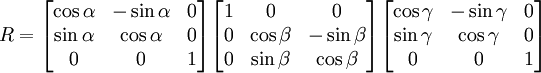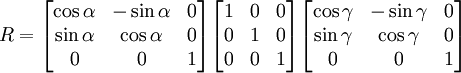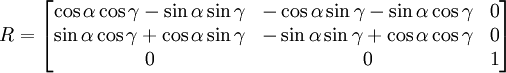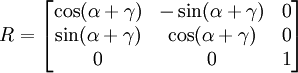Gimbal lock

Blocage de cardan

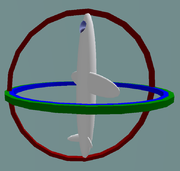
Animation : un ensemble de trois cardans montés de façon à accorder trois degrés de liberté

Le blocage de cardan est la perte d'un degré de liberté, plus connue sous le nom anglais de gimbal lock, qui survient quand les axes de deux des trois cardans nécessaires pour appliquer ou compenser les rotations dans l'espace à trois dimensions sont portés par la même direction.

Un cardan est un anneau fixé de façon à pouvoir tourner autour d'un axe. Les cardans sont souvent imbriqués les uns dans les autres de façon à pouvoir tourner autour de plusieurs axes. Ils apparaissent dans les gyroscopes et dans les centrales à inertie afin de permettre au cardan le plus intérieur de rester fixe alors que la fixation du cardan extérieur peut prendre n'importe quelle orientation, dans les compas, les volants à inertie ou plus familièrement dans des porte-bouteilles pour permettre aux objets de rester horizontaux. Ils servent à orienter les propulseurs d'une fusée^[1]. Certains systèmes de coordonnées mathématiques se comportent comme si des cardans réels étaient utilisés pour mesurer les angles. Lorsqu'il y a au moins trois cardans imbriqués d'une certaine façon, le blocage de cardan peut se produire.

Sommaire

1 Le blocage de cardan en génie mécanique
2 Le blocage de cardan en mathématiques appliquées
- 2.1 Perte d'un degré de liberté avec les angles d'Euler
- 2.2 La solution des quaternions
3 Notes et références
4 Voir aussi
- 4.1 Articles connexes
- 4.2 Liens externes

Le blocage de cardan en génie mécanique

Exemple

Situation normale : les trois cardans sont indépendants

Blocage de cardan : deux des trois cardans sont coplanaires, un degré de liberté est perdu

Prenons le cas d'une plate-forme de mesure de l'altitude sur un avion qui vole vers le Nord disposant de trois axes de cardans à angles droits deux à deux, c'est-à-dire le roulis, le tangage et le lacet, chacun valant zéro. Si l'avion s'incline de 90 degrés vers le haut, l'axe de roulis de l'avion et de la plate-forme devient parallèle à l'axe du cardan de lacet, et on ne peut plus compenser les changements de lacet (voir illustration ci-contre).

Le mot blocage est trompeur : aucun cardan ne se bloque, les trois cardans peuvent toujours tourner librement autour de leurs axes de fixation respectifs. Néanmoins, comme les axes de roulis et de lacet sont parallèles, il n'y a plus d'axe disponible pour réagir aux changements de lacet.

Solutions

On peut pallier le problème en utilisant un quatrième cardan, déplacé de manière intelligente au moyen d'un moteur, de manière à maintenir un grand angle entre les axes de cardans du roulis et du lacet.

Une autre solution consiste à tourner un ou plusieurs cardans vers une position arbitraire au moment où le blocage de cardan est détecté, en réinitialisant ainsi le dispositif.

L'approche moderne est d'éviter complètement d'utiliser des cardans. Dans le contexte de centrales à inertie, cela peut se faire en montant directement les capteurs inertiels au corps du véhicule (plateforme inertielle liée)^[2] et en exploitant les données de rotation et d'accélération ainsi captées en utilisant des méthodes à base de quaternions pour en déduire l'orientation et la vitesse du véhicule. Une autre manière de remplacer les cardans est d'utiliser des supports à fluide ou une chambre de flottaison^[3].

Le blocage de cardan à bord de Apollo 11

Une anecdote bien connue à propos du blocage de cardan concerne la mission lunaire Apollo 11. Sur ce vaisseau spatial, un jeu de cardans était utilisé sur une centrale à inertie. Les ingénieurs étaient avertis du problème du blocage de cardan, mais s'étaient refusé à employer un quatrième cardan^[4]. La justification de ce choix apparaît en partie dans dans la citation suivante :

« Les avantages d'un cardan surnuméraire semblent moins importants que la simplicité de l'équipement, le gain de place, et la fiabilité naturelle d'une unité à trois degrés de liberté directs. »

— David Hoag, Apollo Lunar Surface Journal

Ils ont préféré une solution alternative s'appuyant sur un dispositif qui se serait déclenché à l'approche de 85 degrés de roulis. Ce dispositif n'a pas fonctionné^[5] :

« À l'approche de ce point, au sein d'une boucle de stabilisation fermée, les moteurs de torsion pouvaient en principe être commandés pour faire tourner le cardan de 180 degrés d'un seul coup. Au lieu de cela, dans le module lunaire, l'ordinateur a fait clignoter un avertissement « blocage de cardan » à 70 degrés et a gelé la plate-forme inertielle à 85 degrés »

— Paul Fjeld, Apollo Lunar Surface Journal

Cela a inspiré au pilote du module de commande Mike Collins une fameuse pointe d'humour alors qu'il communiquait par radio avec la Terre :

« Que diriez-vous de m'envoyer un quatrième cardan pour Noël ? »

Le blocage de cardan en mathématiques appliquées

Le problème du blocage de cardan apparaît lorsque l'on utilise les angles d'Euler dans une application des mathematiques, par exemple dans un logiciel (modélisation 3D, système de navigation embarqué, jeu vidéo, métavers, ...).

Les angles d'Euler offrent une description numérique d'une rotation quelconque de l'espace à trois dimensions au moyen de trois nombres.

Pour faire une comparaison, toutes les translations peuvent se décrire au moyen de trois nombres $x$ , $y$ et $z$ comme la succession de trois mouvements en ligne droite le long de trois axes perpendiculaires $X$ , $Y$ et $Z$ . Il en va de même pour les rotations, toutes les rotations peuvent se décrire au moyen de trois nombres $α$ , $β$ et $γ$ , comme la succession de trois mouvements de rotation autour de trois axes perpendiculaires l'un avec le suivant. Cette ressemblance entre les coordonnées linéaires et les coordonnées angulaires rend les angles d'Euler très intuitifs, mais malheureusement ils souffrent du problème du blocage de cardan.

Perte d'un degré de liberté avec les angles d'Euler

Une rotation de l'espace à trois dimensions peut se représenter numériquement au moyen de matrices de plusieurs manières. Une de ces représentations est :

$\begin{align} R &= \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta \\ 0 & \sin \beta & \cos \beta \end{bmatrix} \begin{bmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align}$

avec $α$ et $γ$ contraints dans l'intervalle $[ - π,π]$ et $β$ contraint dans l'intervalle $[0,π]$ .

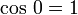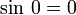Examinons par exemple ce qui se passe lorsque $β = 0$ . Comme $\cos \, 0 = 1$ et $\sin \, 0 = 0$ , l'expression ci-dessus devient égale à :

$\begin{align} R &= \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align}$

La seconde matrice est la matrice identité et n'a pas d'effet sur le produit. Si l'on multiplie la première matrice par la troisième, on obtient :

$\begin{align} R &= \begin{bmatrix} \cos \alpha \cos \gamma -\sin \alpha \sin \gamma & -\cos \alpha \sin \gamma - \sin \alpha \cos \gamma & 0 \\ \sin \alpha \cos \gamma + \cos \alpha \sin \gamma & -\sin \alpha \sin \gamma + \cos \alpha \cos \gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align}$

Enfin, en appliquant les formules de trigonométrie :

$\begin{align} R &= \begin{bmatrix} \cos ( \alpha + \gamma ) & -\sin (\alpha + \gamma) & 0 \\ \sin ( \alpha + \gamma ) & \cos (\alpha + \gamma) & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{align}$

Changer les valeurs de $α$ et de $γ$ dans la matrice ci-dessus a le même effet : l'angle de rotation $α + γ$ change, mais l'axe de rotation reste dans la direction $Z$ . La dernière colonne et la dernière ligne de la matrice ne changeront pas : un degré de liberté a été perdu.

La seule solution pour que $α$ et $γ$ recommencent à jouer des rôles différents est d'éloigner $β$ de la valeur $0$ .

Un problème semblable apparaît lorsque $β = π$ .

On peut choisir d'autres conventions pour représenter une rotation avec une matrice au moyen d'angles d'Euler que la convention Z-X-Z ci-dessus et on peut également choisir d'autres intervalles de variation pour les angles, mais dans tous les cas, il y a au moins une valeur pour laquelle un degré de liberté est perdu.

On remarquera que le problème du blocage de cardan ne rend pas les angles d'Euler « faux » (ils continuent à jouer leur rôle de système de coordonnées), mais les rend mal adaptés à certaines applications pratiques.

La solution des quaternions

Une autre représentation des rotations dans l'espace à trois dimensions est celle des quaternions.

Un quaternion est un quadruplet 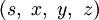$(s,\ x,\ y,\ z)$ qui représente dans le cas général une similitude géometrique. Si la relation $s 2 + x 2 + y 2 + z 2 = 1$ est vérifiée, alors le quaternion peut être utilisé pour représenter une rotation.

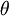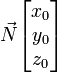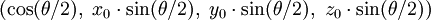D'un point de vue pratique, une rotation d'angle $\mathbf{\theta}$ autour de l'axe dirigé par un vecteur unitaire $\vec{N}\begin{bmatrix}x_0\\ y_0\\ z_0\end{bmatrix}$ est représentée par le quaternion $(\cos (\theta / 2),\ x_0 \cdot \sin (\theta / 2),\ y_0 \cdot \sin (\theta / 2),\ z_0 \cdot \sin (\theta / 2) )$ .

Il n'y a pas de problème équivalent à celui du blocage de cardan avec les quaternions. Cela peut s'expliquer de manière intuitive par le fait qu'un quaternion décrit une rotation en bloc (« veuillez tourner de 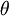$\mathbf{\theta}$ radians autour de l'axe porté par le vecteur 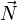$\vec{N}$ »), tandis que les angles d'Euler sont composés de trois rotations successives.

En plus de cela, les quaternions ont d'autres avantages sur les angles d'Euler.

Notes et références

↑ (en)Jonathan Strickland, « What is a gimbal -- and what does it have to do with NASA? », 2008
↑ (en)Chris Verplaetse, « Overview of Pen Design and Navigation Background », 1995
↑ (en)Chappell, Charles, D., « Articulated gas bearing support pads », 2006
↑ (en)David Hoag, « Apollo Guidance and Navigation - Considerations of Apollo IMU Gimbal Lock - MIT Instrumentation Laboratory Document E-1344 », 1963
↑ (en)Eric M. Jones et Paul Fjeld, « Gimbal Angles, Gimbal Lock, and a Fourth Gimbal for Christmas », 2006

Voir aussi

Liens externes

(en)Vidéo expliquant le blocage de cardan au moyen d'une animation

Portail de l’astronautique

Ce document provient de « Blocage de cardan ».

Catégories : Angle | Mesure physique | Technologie des véhicules spatiaux | Imagerie numérique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Gimbal lock de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Gimbal Lock — (engl.) bzw. kardanische Blockade bezeichnet ein geometrisches Problem, welches bei Transformationen in Verbindung mit Eulerwinkeln auftreten kann. Der Begriff stammt aus dem Englischen, Gimbal heißt hier Kardanische Aufhängung, Gimbal Lock ist… … Deutsch Wikipedia
Gimbal lock — bezeichnet ein geometrisches Problem, welches bei Transformationen in Verbindung mit Eulerwinkeln auftreten kann. Der Begriff stammt aus dem Englischen, Gimbal heißt hier Kardanische Aufhängung, Gimbal Lock ist also deren Blockade. Eulerwinkel… … Deutsch Wikipedia
Gimbal lock — occurs when the axes of two of the three gimbals needed to compensate for rotations in three dimensional space are driven to the same direction. For example, assume a level sensing platform on an aircraft flying due north has its three gimbal… … Wikipedia
gimbal lock — A situation in which two gimbals coincide in the same plane. This results in the restriction on the freedom of movement of a gyroscope, robbing it of its useful properties. Inner and outer gimbals are in the same plane … Aviation dictionary
Gimbal — A gimbal is a pivoted support that allows the rotation of an object about a single axis. A set of two gimbals, one mounted on the other with pivot axes orthogonal, may be used to allow an object mounted on the innermost gimbal to remain vertical… … Wikipedia
Складывание рамок — … Википедия
Inertial navigation system — An Inertial Navigation System (INS) is a navigation aid that uses a computer and motion sensors to continuously track the position, orientation, and velocity (direction and speed of movement) of a vehicle without the need for external references … Wikipedia
Euler angles — The Euler angles were developed by Leonhard Euler to describe the orientation of a rigid body (a body in which the relative position of all its points is constant) in 3 dimensional Euclidean space. To give an object a specific orientation it may… … Wikipedia
Blocage de cardan — Animation : un ensemble de trois cardans montés de façon à accorder trois degrés de liberté Le blocage de cardan est la perte d un degré de liberté, connue aussi sous le nom anglais de gimbal lock, qui survient quand les axes de deux des… … Wikipédia en Français
Eulerwinkel — Eulersche Winkel oder auch Eulerwinkel sind eine Möglichkeit zur Beschreibung der Orientierung (Winkellage) von Objekten im dreidimensionalen Raum. Es handelt sich um drei Winkel, welche jeweils eine Drehung (Rotation) um bestimmte Achsen… … Deutsch Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Gimbal lock

Blocage de cardan

Sommaire