Formules de binet

Formules de binet

Formules de Binet

En physique, en mécanique classique, les formules de Binet sont des expressions de la vitesse et de l'accélération d'un corps soumis à une force centrale telle que la gravitation ou un champ électrostatique.

Elles permettent d'exprimer, en coordonnées polaires, la position d'un mobile en fonction de l'angle formé par celui-ci. En effet, l'expression en fonction du temps est beaucoup plus difficile à établir. En particulier, les formules de Binet permettent de démontrer que, dans un champ de force centrale en K/r², les trajectoires sont des coniques.

Formules de Binet

On considère tout d'abord le cas attractif. En posant u = 1/r et en notant 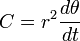C = r^2 \frac{d\theta}{dt}\; la constante des aires, d'après la seconde loi de Kepler, on peut montrer que :

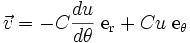\vec{v} = -C\frac{du}{d\theta}\; \mathrm{e_r} + C u\; \mathrm{e_{\theta}} ;
\vec{a} = -C^2 u^2 \left[ \frac{d^2u}{d\theta^2} + u \right]\; \mathrm{e_r}.

L'accélération est donc radiale comme la force à laquelle est soumise le corps. Dans le cas répulsif, les composantes selon er seraient positives, le corps étudié s'éloignerait du centre de force.

Démonstration

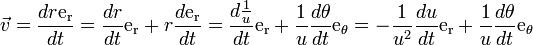
On a \vec{v} = \frac{dr\mathrm{e_r}}{dt} = \frac{dr}{dt}\mathrm{e_r} + r \frac{d\mathrm{e_r}}{dt} = \frac{d\frac{1}{u}}{dt}\mathrm{e_r}+\frac{1}{u}\frac{d\theta}{dt}\mathrm{e_{\theta}} = -\frac{1}{u^2}\frac{du}{dt}\mathrm{e_r}+\frac{1}{u}\frac{d\theta}{dt}\mathrm{e_{\theta}}

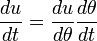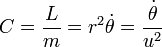
Or \frac{du}{dt} = \frac{du}{d\theta}\frac{d\theta}{dt} et C = \frac{L}{m} =r^2\dot\theta = \frac{\dot\theta}{u^2}

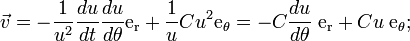
Donc \vec{v} = -\frac{1}{u^2}\frac{du}{dt}\frac{du}{d\theta}\mathrm{e_r} + \frac{1}{u}Cu^2\mathrm{e_{\theta}} = -C\frac{du}{d\theta}\; \mathrm{e_r} + C u\; \mathrm{e_{\theta}};

De même on dérive \vec{v} pour obtenir \vec{a}.

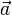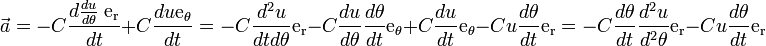
\vec{a} = -C\frac{d\frac{du}{d\theta}\; \mathrm{e_r}}{dt} + C\frac{du\mathrm{e_{\theta}}}{dt} = -C\frac{d^2u}{dtd\theta}\mathrm{e_r}-C\frac{du}{d\theta}\frac{d\theta}{dt}\mathrm{e_{\theta}} + C\frac{du}{dt}\mathrm{e_{\theta}} - Cu\frac{d\theta}{dt}\mathrm{e_r} = -C\frac{d\theta}{dt}\frac{d^2u}{d^2\theta}\mathrm{e_r} - Cu\frac{d\theta}{dt}\mathrm{e_r} = -C^2 u^2 \left[ \frac{d^2u}{d\theta^2} + u \right]\; \mathrm{e_r}

Trajectoires coniques

On considère ici le cas attractif, le cas répulsif donnant exactement le même résultat. En utilisant la seconde loi de Newton, on a :

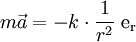m \vec{a} = -k \cdot \frac{1}{r^2}\; \mathrm{e_r}.

En insérant l'expression de l'accélération et en remplaçant 1/r par u, puis enfin en projetant selon er, on a :

m C^2 \left[ \frac{d^2u}{d \theta^2} + u \right] = k, soit encore :
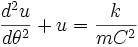\frac{d^2u}{d \theta^2} + u = \frac{k}{mC^2}.

Cette équation différentielle s'intègre facilement : c'est un oscillateur harmonique. On obtient :

u(θ) = Acos(θ + φ) + B.

En revenant à l'expression de r, on a :

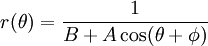r(\theta) = \frac{1}{B + A \cos(\theta + \phi)}.

C'est bien l'expression d'une conique en coordonnées polaires, dont la nature exacte - parabole, hyperbole ou ellipse - dépend des conditions initiales.

  • Portail de la physique Portail de la physique
Ce document provient de « Formules de Binet ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formules de binet de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Formules De Binet — En physique, en mécanique classique, les formules de Binet sont des expressions de la vitesse et de l accélération d un corps soumis à une force centrale telle que la gravitation ou un champ électrostatique. Elles permettent d exprimer, en… …   Wikipédia en Français

  • Formules de Binet —  Ne pas confondre avec la formule de Binet sur la suite de Fibonacci. En physique, en mécanique classique, les formules de Binet sont des expressions de la vitesse et de l accélération d un corps soumis à une force centrale telle que la… …   Wikipédia en Français

  • Formule de Binet — Formules de Binet En physique, en mécanique classique, les formules de Binet sont des expressions de la vitesse et de l accélération d un corps soumis à une force centrale telle que la gravitation ou un champ électrostatique. Elles permettent d… …   Wikipédia en Français

  • Jacques Philippe Marie Binet — Pour les articles homonymes, voir Binet. Jacques Binet Jacques Philippe Marie Binet Naissance 2 février 1786 …   Wikipédia en Français

  • Liste Des Équations Et Formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X …   Wikipédia en Français

  • Liste des equations et formules — Liste des équations et formules Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H …   Wikipédia en Français

  • Liste des équations et formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X …   Wikipédia en Français

  • Liste d'équations et formules — Ceci est une Liste des équations et formules par ordre alphabétique. Cette liste contient les équations, les formules, les relations et autres identités, égalités ou inégalités. Sommaire : Haut A B C D E F G H I J K L M N O P Q R S T U V W X …   Wikipédia en Français

  • Force Centrale En 1/r⁵ — En physique, en mécanique classique, il s agit d un résultat établi par Isaac Newton, en corollaire de son exégèse des Principia Naturalis. Énoncé Soit un point matériel P de masse m décrivant une trajectoire circulaire de rayon a et de centre C …   Wikipédia en Français

  • Force centrale en 1/r⁵ — En physique, en mécanique classique, il s agit d un résultat établi par Isaac Newton, en corollaire de son exégèse des Principia Naturalis. Énoncé Soit un point matériel P de masse m décrivant une trajectoire circulaire de rayon a et de centre C …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”