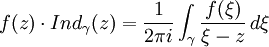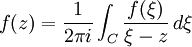Formule intégrale de cauchy

Formule intégrale de Cauchy

Pour les articles homonymes, voir Cauchy.

La formule intégrale de Cauchy est un point essentiel de l'analyse complexe. Elle exprime le fait que la valeur en un point d'une fonction holomorphe est complètement déterminée par les valeurs qu'elle prend sur un chemin fermé contenant (c'est-à-dire entourant) ce point. Elle peut aussi être utilisée pour exprimer sous forme d'intégrales toutes les dérivées d'une fonction holomorphe.

Expression

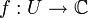Supposons que U soit un ouvert connexe du plan complexe $\mathbb C$ , que $f:U\rightarrow \mathbb C$ soit une fonction holomorphe sur U. Soit $γ$ un chemin fermé inclus dans U, soit enfin z n'appartenant pas à ce chemin. On a alors la formule suivante:

$f(z)\cdot Ind_\gamma (z) = {1 \over 2\pi i} \int_\gamma {f(\xi) \over \xi-z}\, d\xi$

où $I n d γ (z)$ désigne l'indice du point $z$ par rapport au chemin $γ$ . Cette formule est particulièrement utile dans le cas où $γ$ est un cercle C orienté positivement, contenant z et inclus dans U. En effet, l'indice de $z$ par rapport à C vaut alors $1$ , d'où :

$f(z) = {1 \over 2\pi i} \int_C {f(\xi) \over \xi-z}\, d\xi$

Principale conséquence

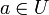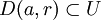Montrons que ceci implique que f est développable en série entière sur U : soit $a\in U$ , $r > 0$ tel que $D(a,r)\subset U$ .

Soit 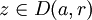$z\in D(a,r)$ , et $γ$ le cercle de centre a et de rayon r orienté positivement paramétré par $\theta\in[0,2\pi]$ .

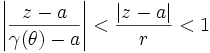On a pour tout $\theta\in[0,2\pi]$ : $\left|\frac{z-a}{\gamma(\theta)-a}\right|<\frac{|z-a|}{r}<1$ ,
ce qui prouve la convergence uniforme sur $[0,2π]$ de la série de terme général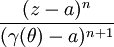 $\frac{(z-a)^n}{(\gamma(\theta)-a)^{n+1}}$ vers

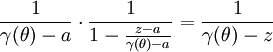$\frac{1}{\gamma(\theta)-a}\cdot\frac{1}{1-\frac{z-a}{\gamma(\theta)-a}}=\frac{1}{\gamma(\theta)-z}$ ,

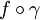et comme $f\circ \gamma$ est continue sur $[0,2π]$ compact, donc bornée, on a convergence uniforme de la série

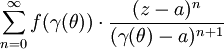$\sum_{n=0}^\infty f(\gamma(\theta))\cdot\frac{(z-a)^n}{(\gamma(\theta)-a)^{n+1}}$ sur $[0,2π]$ ,
ce qui permet d'effectuer une inversion des signes sommes: on a ainsi pour tout z dans D(a,r):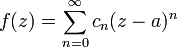

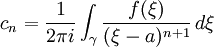
$f(z) = \sum _{n=0}^\infty c_n(z-a)^n$ avec $c_n= {1 \over 2\pi i} \int_\gamma {f(\xi) \over (\xi-a)^{n+1}}\, d\xi$

et donc f est analytique sur U. On a supposé dans la démonstration que U était connexe, mais le fait d'être analytique étant une propriété locale, on peut généraliser l'énoncé précédent et affirmer que toute fonction holomorphe sur un ouvert U quelconque est analytique sur U.

On remarque aussi que, en donnant une expression aux coefficients du développement de f, cette formule explicite les dérivées n-ièmes de f en a:

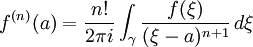$f^{(n)}(a) = {n! \over 2\pi i} \int_\gamma {f(\xi) \over (\xi-a)^{n+1}}\, d\xi$ .

Démonstration de la formule

La preuve de cette formule est assez simple: pour la montrer en un $z 0$ donné il suffit d'appliquer le théorème intégral de Cauchy à la fonction g ainsi définie : 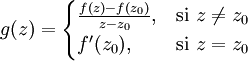$g(z)=\begin{cases} \frac{f(z)-f(z_0)}{z-z_0}, & \text{si }z\neq z_0 \\ f'(z_0), & \text{si }z=z_0 \end{cases}$ et de développer le résultat obtenu.

Autres conséquences

Cette formule a de nombreuses applications, outre le fait de montrer que toute fonction holomorphe est analytique, et permet notamment de montrer le principe du maximum et le théorème des résidus.

Portail des mathématiques

Ce document provient de « Formule int%C3%A9grale de Cauchy ».

Catégories : Analyse complexe | Théorie de l'intégration

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule intégrale de cauchy de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Formule Intégrale De Cauchy — Pour les articles homonymes, voir Cauchy. La formule intégrale de Cauchy est un point essentiel de l analyse complexe. Elle exprime le fait que la valeur en un point d une fonction holomorphe est complètement déterminée par les valeurs qu elle… … Wikipédia en Français
Formule integrale de Cauchy — Formule intégrale de Cauchy Pour les articles homonymes, voir Cauchy. La formule intégrale de Cauchy est un point essentiel de l analyse complexe. Elle exprime le fait que la valeur en un point d une fonction holomorphe est complètement… … Wikipédia en Français
Formule intégrale de Cauchy — Pour les articles homonymes, voir Cauchy. La formule intégrale de Cauchy est un point essentiel de l analyse complexe. Elle exprime le fait que la valeur en un point d une fonction holomorphe est complètement déterminée par les valeurs qu elle… … Wikipédia en Français
Formule de Binet-Cauchy — Pour les articles homonymes, voir Cauchy et Binet. En algèbre linéaire, la formule de Binet Cauchy généralise la propriété de multiplicativité du déterminant d un produit au cas de deux matrices rectangulaires. On peut l écrire pour des matrices… … Wikipédia en Français
Integrale curviligne — Intégrale curviligne En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
Intégrale Curviligne — En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
formule — [ fɔrmyl ] n. f. • 1496; fourmulle 1372; lat. formula, dimin. de forma → forme I ♦ Forme déterminée que l on est tenu ou que l on est convenu de respecter pour exprimer une idée, énoncer une règle ou exposer un fait. 1 ♦ Dr. Modèle qui contient… … Encyclopédie Universelle
Cauchy — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Cette page d’homonymie répertorie des personnes (réelles ou fictives) partageant un même patronyme. Patronyme Augustin Louis Cauchy (1789 1857),… … Wikipédia en Français
Intégrale curviligne — En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
Théorème de Cauchy-Lipschitz — Pour les articles homonymes, voir Cauchy. Cauchy développe une première version du théorème de l article. En mathématiques, et plus précisément en a … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formule intégrale de cauchy