Formule de MacCullagh

Formule de MacCullagh
James MacCullagh (1809–1847)

La formule de MacCullagh est une importante formule pour décrire le champ de gravité d'un corps non sphérique à une distance suffisamment grande mais pas très grande par rapport aux dimensions linéaires du corps. Elle s'obtient en partant de la définition de base du potentiel gravifique, sans effectuer un développement général de Laplace dont elle représente un cas particulier limité à une approximation d'ordre 2. Elle est très utilisée en géodésie théorique et en géophysique.

Sommaire

Expression générale du potentiel gravifique

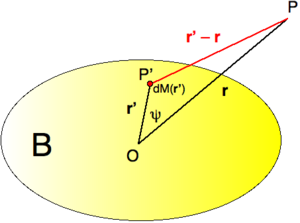
MacCullagh 1.png

En coordonnées sphériques, désignons la composante radiale du vecteur-position \mathbf{r} d'un point potentié P par r, et celle du vecteur-position \mathbf{r'} d'un point potentiant P' par r'. L'origine O du système de coordonnées est pour le moment encore arbitraire. L'angle compris entre les vecteurs \mathbf{r} et \mathbf{r'} est noté ψ et l'élément de masse en P' est \mathrm dM(\mathbf{r'}), la masse totale du corps B étant M. Sous ces conditions, le potentiel gravifique[1] V(P) engendré au point P par le corps B peut s'écrire en toute généralité

V(P) = G \int_{M} \frac{1}{\|\mathbf{r'} - \mathbf{r}\|}\, \mathrm dM(\mathbf{r'}),

avec

\|\mathbf{r'} - \mathbf{r}\| = r \sqrt{1 - 2\frac{r'}{r}\cos \psi + \left(\frac{r'}{r}\right)^{2}} .

La constante G dénote la constante de gravitation de Newton.

Comme (1 + x) − 1 / 2 = 1 − x / 2 + 3x2 / 8 + o(x3) lorsque -1 \le x \le +1, on trouve[2], en posant x = − 2(r' / r)cos ψ + (r' / r)2 :

\frac{1}{\sqrt{1 - 2 \frac{r'}{r} \cos \psi + \left(\frac{r'}{r}\right)^2}} = 1 + \frac{r'}{r} \cos \psi - \frac{1}{2} \left(\frac{r'}{r}\right)^2 + \frac{3}{2} \left(\frac{r'}{r}\right)^2 \cos^2\psi + o\left[\left(\frac{r'}{r}\right)^3\right].

Par conséquent, on a[3]

\frac{r}{\|\mathbf{r'} - \mathbf{r}\|} = 1 + \frac{r'}{r} \cos \psi + \left(\frac{r'}{r}\right)^2 - \frac32 \left(\frac{r'}{r}\right)^2 \sin^2\psi + \dots .

Le potentiel gravifique en P est donc

V(P) = \frac Gr \int_M \mathrm dM + \frac G{r^2} \int_M r' \cos \psi \mathrm dM + \frac G{r^3} \int_M r'^2 \mathrm dM - \frac{3G}{2r^3} \int_M r'^2 \sin^2\psi \mathrm dM + \dots

Théorème de MacCullagh

On voit ainsi qu'à l'approximation d'ordre 2, le potentiel gravifique V(P) peut se décomposer en quatre termes distincts V0(P), V1(P), V2(P), V3(P), soit

V(P) = V0(P) + V1(P) + V2(P) + V3(P).

Le premier terme,

V_0 = G r^{-1} \int_M\, \mathrm dM = GM r^{-1},

correspond au potentiel d'une distribution sphérique, lequel est le même que celui d'une masse ponctuelle égale à la masse comprise dans toute la sphère. A grande distance, c'est évidemment le terme dominant, puisque sa décroissance en 1/r est plus lente que celle des autres termes. C'est le potentiel newtonien classique utilisé pour établir les trajectoires keplériennes des planètes. On dit de lui qu'il correspond à un monopôle, ou à une distribution de masse monopolaire.

MacCullagh 2.png

Le deuxième terme,

V_1 = G r^{-2} \int_M r' \cos \psi\, \mathrm dM,

correspond à une distribution de masse dipolaire, autrement dit à un dipôle. En choisissant l'origine des coordonnées au centre de masse du corps, on annule ce terme[4]. En effet, en se référant à la figure ci-contre, on peut écrire

V_1 = G r^{-2} \int_M r' \cos \psi\, \mathrm dM = G r^{-2} \int_M x\, \mathrm dM = G M r^{-2} x_0,

où x0 désigne la composante le long d'un axe Ox de la position du centre de masse.

Les troisième et quatrième termes, V2 et V3, se rapportent à une distribution de masse quadrupolaire, autrement dit à un quadrupôle. Pour V2 on trouve successivement[5]

V_2 = G r^{-3} \int_M r'^2 \, \mathrm dM = G r^{-3} \int_M (x^2+y^2+z^2) \mathrm dM = \frac12 G r^{-3} \int_M [(y^2+z^2)+(x^2+z^2)+(x^2+y^2)] \, \mathrm dM = \frac12 G r^{-3} (A+B+C),

où A, B, C désignent les trois moments d'inertie par rapport aux axes Ox, Oy, Oz, respectivement. En définissant le moment d'inertie moyen \bar I par

\bar I = \frac13 (A+B+C),

on a donc

V_2 = \frac32 G r^{-3} \bar I.

Pour V3, on trouve

V_3 = -\frac32 G r^{-3} \int_M r'^2 \sin^2 \psi\, \mathrm dM = -\frac32 G r^{-3} \int_M r'^2 \cos^2 \alpha\, \mathrm dM = \frac32 G r^{-3} I,

où I est le moment d'inertie autour de la direction OP. On aboutit ainsi à la formule (parfois aussi appelée théorème) de MacCullagh :

V(P) = G M r^{-1} - \frac32 G r^{-3} (I - \bar I).

Celle-ci s'applique très utilement à des corps presque sphériques comme la Terre et les planètes, et c'est une approximation encore valable à distance suffisante pour un corps de symétrie quelconque. Il existe évidemment une limitation implicite à sa validité par le fait que la série a été tronquée à l'ordre 2 : des harmoniques supérieurs au degré 2 sont bien sûr nécessaires pour représenter de manière plus précise le champ de gravité extérieur en toute généralité.

Formule de MacCullagh pour les corps à symétrie de révolution

Le moment d'inertie I autour d'un axe passant par le centre de masse O d'un corps peut s'écrire en termes des moments principaux d'inertie A, B, C obtenus par diagonalisation préalable de la matrice 3x3 représentant le tenseur d'inertie au moyen de la relation

I = n_x^2 A + n_y^2 B + n_z^2 C.

Ici, nx, ny, nz désignent les cosinus directeurs de l'axe OP par rapport aux axes principaux d'inertie Ox, Oy, Oz, respectivement.

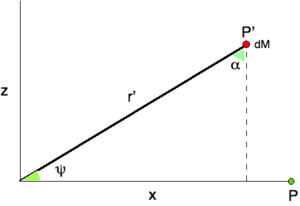
En faisant l'hypothèse que le corps est de révolution autour de l'axe Oz, c'est-à-dire qu'il possède une symétrie axiale d'axe Oz, on a A = B. Désignons par ϕ l'angle que fait la direction OP avec le plan Oxy.[6] Alors nz = sin ϕ et, à cause de la relation liant n_x^2 + n_y^2 + n_z^2 = 1 les cosinus directeurs, on trouve

\sin^2 \phi = 1 - n_x^2 - n_y^2.

Avec A = B, la formule de MacCullagh devient

V(P) = GM r^{-1} - \frac12 G r^{-3} (3 I - 2 A - C).

Dans le cas d'une symétrie axiale, le moment d'inertie I prend lui-même la forme

I = A (n_x^2+n_y^2) + C \sin^2 \phi = A (1 - \sin^2 \phi) + C \sin^2 \phi.

La formule de MacCullagh, pour un corps de révolution, prend donc finalement[7] la forme suivante :

V(P) = GM r^{-1} + \frac12 G r^{-3} (C - A) (1 - 3 \sin^2 \phi).

Facteur de forme géodynamique

D'autre part, toujours dans l'hypothèse d'une symétrie axiale, le développement général du potentiel gravifique en multipôles limité aux termes d'ordre 2 s'écrit

V(P) = GMr − 1 − J2GMa2r − 3P2(cos θ),

où

P_2 (\cos \theta) = \frac32 \sin^2 \phi - \frac12 ,

est le polynôme de Legendre de degré 2. On a donc

V(P) = GM r^{-1} - \frac12 J_2 GM a^2 r^{-3} (1 - 3 \sin^2 \phi).

Dans le cas de la Terre, le coefficient géopotentiel zonal de degré 2, à savoir J2, est souvent appelé « facteur de forme géodynamique ». On l'obtient par identification de cette dernière formule avec celle de MacCullagh, soit

J_2 = \frac{C - A}{Ma^2}.

Certains géodésiens appellent aussi cette dernière relation « formule de MacCullagh », mais cet usage ne semble pas très judicieux.

Notes

  1. ↑ On définit ici le potentiel gravifique V comme un travail. En physique, on a plutôt coutume de définir le potentiel gravifique comme une énergie d'interaction Φ, de sorte que Φ = − V.
  2. ↑ \textstyle\frac{1}{\sqrt{1 - 2 \frac{r'}{r} \cos \psi + \left(\frac{r'}{r}\right)^2}} = 1 - \frac12\left[- 2 \frac{r'}{r} \cos \psi + \left(\frac{r'}{r}\right)^2\right] + \frac{3}{8}\left[- 2 \frac{r'}{r} \cos \psi + \left(\frac{r'}{r}\right)^2\right]^2 + \dots \textstyle = 1 + \frac{r'}{r} \cos \psi - \frac12 \left(\frac{r'}{r}\right)^2 + \frac38 \left[4 \left(\frac{r'}{r}\right)^2 \cos^2\psi - 4 \left(\frac{r'}{r}\right)^3 \cos \psi + \left(\frac{r'}{r}\right)^4\right] + \dots \textstyle = 1 + \frac{r'}{r} \cos \psi - \frac{1}{2} \left(\frac{r'}{r}\right)^2 + \frac{3}{2} \left(\frac{r'}{r}\right)^2 \cos^2\psi + o\left[\left(\frac{r'}{r}\right)^3\right]
  3. ↑ \textstyle\frac{r}{\|\mathbf{r'} - \mathbf{r}\|} = 1 + \frac{r'}{r} \cos \psi + \frac{1}{2} \left(\frac{r'}{r}\right)^2 (3 \cos^2\psi - 1) + \dots = 1 + \frac{r'}{r} \cos \psi + \frac{1}{2} \left(\frac{r'}{r}\right)^2 (3 - 3 \sin^2\psi - 1) + \dots \textstyle = 1 + \frac{r'}{r} \cos \psi + \left(\frac{r'}{r}\right)^2 - \frac{3}{2} \left(\frac{r'}{r}\right)^2 \sin^2\psi + \dots .
  4. ↑ Ainsi, on arrive à déterminer avec précision le centre de masse de la Terre en déterminant (par approximations successives) le référentiel dans lequel les coefficients dipolaires du champ de gravité s'annulent.
  5. ↑ On repère ici, sans perte de généralité, la position d'un point quelconque du corps B par des coordonnées cartésiennes x, y, z.
  6. ↑ Dans un contexte géophysique, l'angle ϕ représente en général la latitude du lieu, ou en est très proche.
  7. ↑ V(P) = GM r^{-1} - \frac12 G r^{-3} (3 I - 2 A - C) = GM r^{-1} - \frac12 G r^{-3} (3 A - 3 A \sin^2 \phi + 3 C \sin^2 \phi - 2 A - C) = GM r^{-1} - \frac12 G r^{-3} [A - C - 3 (A - C) \sin^2 \phi] = GM r^{-1} + \frac12 G r^{-3} (C - A) (1 - 3 \sin^2 \phi).

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule de MacCullagh de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Formule De MacCullagh — James MacCullagh (1809–1847) La formule de MacCullagh est une importante formule pour décrire le champ de gravité d un corps non sphérique à une distance suffisamment grande mais pas très grande par rapport aux dimensions linéaires du corps. Elle …   Wikipédia en Français

  • Formule de maccullagh — James MacCullagh (1809–1847) La formule de MacCullagh est une importante formule pour décrire le champ de gravité d un corps non sphérique à une distance suffisamment grande mais pas très grande par rapport aux dimensions linéaires du corps. Elle …   Wikipédia en Français

  • MacCullagh — James MacCullagh James MacCullagh (1809–1847) James MacCullagh (né en 1809 et mort le 24 octobre 1847) était un mathématicien irlandais. Il est l auteur de la Formule de MacCullagh. Né à Landahaussy, à côté de Strabane, dans le …   Wikipédia en Français

  • James MacCullagh — Naissance 1809 Landahaussy (Irlande) Décès 24 octobre 1847 Dublin (Irlande) Nationalité …   Wikipédia en Français

  • Electromagnétisme: lois locales et intégrales — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Equations de Maxwell — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Formulaire d'électromagnétisme — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Lois de Maxwell — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Maxwell-Faraday — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Équation de Maxwell — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”