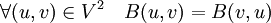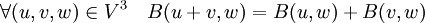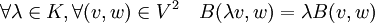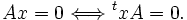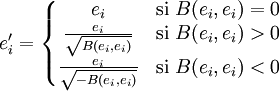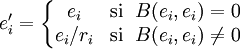Forme bilineaire symetrique

Forme bilinéaire symétrique

Une forme bilinéaire symétrique est le nom donné à une forme bilinéaire sur un espace vectoriel qui est symétrique. Les formes bilinéaires symétriques jouent un rôle important dans l'étude des quadriques.

Sommaire

1 Définition
2 Représentation matricielle
3 Orthogonalité et singularité
4 Bases orthogonales
5 Voir aussi
6 Références

Définition

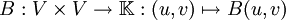Soit $V$ un espace vectoriel de dimension $n$ sur un corps commutatif $\mathbb{K}$ . Une application $B : V\times V\rightarrow \mathbb{K}:(u,v)\mapsto B(u,v)$ est une forme bilinéaire symétrique sur l'espace si:

$\forall (u,v) \in V^2\quad B(u,v)=B(v,u)\$
$\forall (u,v,w) \in V^3 \quad B(u+v,w)=B(u,w)+B(v,w)\$
$\forall \lambda \in K,\forall (v,w) \in V^2 \quad B(\lambda v,w)=\lambda B(v,w)\$

Remarque: Les deux derniers axiomes impliquent seulement la linéarité par rapport à la « première variable » mais le premier permet d'en déduire la linéarité par rapport à la « deuxième variable ».

Représentation matricielle

Soit 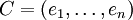$C=(e_{1},\ldots,e_{n})$ une base d'un espace vectoriel $V$ . Définissons la matrice d'ordre $n$ $A$ par $a i j = B (e i, e j)$ . La matrice $A$ est symétrique d'après la symétrie de la forme bilinéaire. Si la matrice de type $(n,1)$ $x$ représente les coordonnées d'un vecteur $v$ par rapport à cette base, et de façon analogue $y$ représente les coordonnées d'un vecteur $w$ , alors $B (v, w)$ est égal à :

t x A y = t y A x .

Supposons que 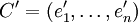$C'=(e'_{1}, \ldots, e'_{n})$ soit une autre base de $V$ , considérons la matrice de passage (inversible) $S$ d'ordre $n$ de la base $C$ à la base $C'$ . Maintenant dans cette nouvelle base la représentation matricielle de la forme bilinéaire symétrique est donnée par

A' = t S A S .

Orthogonalité et singularité

Une forme bilinéaire symétrique est toujours réflexive. Par définition, deux vecteurs $v$ et $w$ sont orthogonaux pour la forme bilinéaire $B$ si $B (v, w) = 0$ , ce qui, grâce à la réflexivité, est équivalent à $B (w, v) = 0$ .

Le noyau d'une forme bilinéaire $B$ est l'ensemble des vecteurs orthogonaux à tout autre vecteur de $V$ . Il est facile de vérifier qu'il est un sous-espace de $V$ . Lorsque nous travaillons avec une représentation matricielle de $A$ relativement à une certaine base, un vecteur $v$ représenté par sa matrice colonne des coordonnées $x$ , appartient au noyau si et seulement si

$A x=0 \Longleftrightarrow {}^t x A=0.$

La matrice $A$ est non inversible ou singulière si et seulement si le noyau de $B$ est non réduit au singleton vecteur nul, c'est-à-dire non trivial.

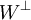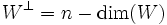Si $W$ est un sous-espace vectoriel de $V$ , alors $W^{\perp}$ , l'ensemble de tous les vecteurs orthogonaux à tout vecteur de $W$ est aussi un sous-espace de $V$ . Lorsque le noyau de $B$ est trivial, la dimension de $W^{\perp}=n-\dim(W)$ .

Bases orthogonales

Une base 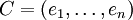$C=(e_{1},\ldots,e_{n})$ est othogonale pour $B$ si :

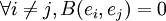$\forall i\neq j, B(e_{i},e_{j})=0\$ .

Lorsque la caractéristique du corps est différente de deux, il existe toujours une base orthogonale. Cela peut être démontré par récurrence.

Une base $C$ est othogonale si et seulement si la matrice $A$ représentant $B$ dans cette base est une matrice diagonale.

Signature et loi d'inertie de Sylvester

Dans sa forme la plus générale, la loi d'inertie de Sylvester affirme, qu'en travaillant sur un corps ordonné $\mathbb{K}$ , le nombre d'éléments diagonaux nuls, ou strictement positifs, ou strictement négatifs, est indépendant de la base orthogonale choisie. Ces trois nombres constituent la signature de la forme bilinéaire.

Cas réel

En travaillant sur le corps des réels, il est possible d'aller un peu plus loin. Soit 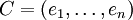$C=(e_{1},\ldots,e_{n})$ une base orthogonale.

Définissons une nouvelles base 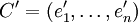$C'=(e'_{1},\ldots,e'_{n})$ par

$e'_{i} = \left\{ \begin{matrix} e_{i} & \mbox{si } B(e_{i},e_{i})=0 \\ \frac{e_{i}}{\sqrt{B(e_{i},e_{i})}} & \mbox{si } B(e_{i},e_{i}) >0\\ \frac{e_{i}}{\sqrt{-B(e_{i},e_{i})}}& \mbox{si } B(e_{i},e_{i}) <0 \end{matrix}\right.$

Maintenant, la matrice $A$ représentant la forme bilinéaire symétrique, dans cette nouvelle base, est une matrice diagonale ayant des 0 ou des 1 uniquement sur sa diagonale. Des zéros apparaissent sur la diagonale si et seulement si le noyau est non trivial.

Cas complexe

En travaillant sur le corps des nombres complexes, on peut établir un résultat similaire à celui du cas réel.

Soit 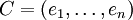$C=(e_{1},\ldots,e_{n})$ une base orthogonale.

Pour tout 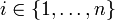$i\in\{1, \ldots, n\}$ tel que 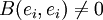$B(e_{i},e_{i})\neq 0$ , notons $r i$ l'une des racines carrées de $B (e i, e i)$ .

Définissons une nouvelle base 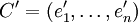$C'=(e'_{1},\ldots,e'_{n})$ par

$e'_{i} = \left\{ \begin{matrix} e_{i} & \mbox{si }\; B(e_{i},e_{i})=0 \\ e_{i}/r_i & \mbox{si }\; B(e_{i},e_{i}) \neq 0\\ \end{matrix}\right.$

Maintenant, la matrice $A$ dans la nouvelle base est une matrice diagonale ayant seulement des 0 ou 1 sur la diagonale. Des zéros apparaissent si et seulement si le noyau est non trivial.

Voir aussi

Forme bilinéaire
Forme hermitienne

Références

Loi d'inertie de Sylvester (en)
Formes quadratiques et groupes classiques de René Deheuvels. Éditions puf. (fr)

Portail des mathématiques

Ce document provient de « Forme bilin%C3%A9aire sym%C3%A9trique ».

Catégorie : Algèbre bilinéaire

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Forme bilineaire symetrique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires: