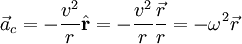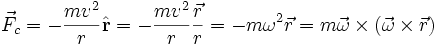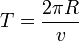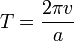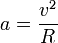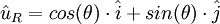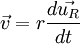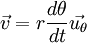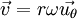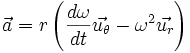- Force centripède
-
Force centripète
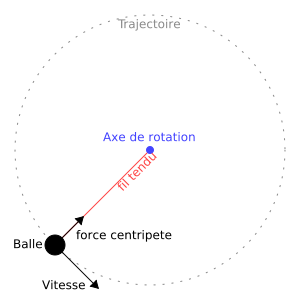 Une balle accrochée par un fil tourne autour d'un axe. La force centripète est exercée par le fil sur la balle pour la maintenir en rotation sur la trajectoire spécifiée. C'est cette force qui donne au fil sa tension.
Une balle accrochée par un fil tourne autour d'un axe. La force centripète est exercée par le fil sur la balle pour la maintenir en rotation sur la trajectoire spécifiée. C'est cette force qui donne au fil sa tension.
Le terme force centripète ("qui tend à rapprocher du centre", en latin) désigne une force permettant de maintenir un objet dans une trajectoire elliptique. En effet, tout objet décrivant une trajectoire elliptique possède en coordonnées cylindriques une accélération radiale non nulle, appelée accélération centripète, qui est dirigée vers le centre de courbure. D'un point de vue dynamique, le Principe Fondamental (PFD) indique alors la présence d'une force radiale dirigée elle aussi vers le centre de courbure.
Cette force est au sens de Newton une force réelle, qui pourra avoir diverses origines, par exemple :
- force de gravitation (mouvement des planètes)
- force de tension (mouvement sur un plan horizontal d'une masse accrochée à un fil dont une extrémité est fixe)
Sans force centripète, l'objet quitterait sa trajectoire elliptique, ce qui se comprend pratiquement par la présence de la force centrifuge. Une force centripète apparaît donc comme une force s'opposant aux effets de la force centrifuge. Il convient néanmoins de préciser que la force centrifuge est une force fictive (voir l'article sur le sujet).
Pour éviter la difficulté relative à la force centrifuge, on pourra considérer que dans un référentiel galiléen un corps isolé adopte une trajectoire rectiligne uniforme. Pour dévier constamment le corps de sa trajectoire rectiligne et lui faire parcourir une trajectoire elliptique, il faudra lui appliquer à tout instant une force compensant l'accélération centrifuge dans le Principe Fondamental, cette force étant alors qualifiée de centripète. Le caractère centripète d'une force n'est donc pas intrinsèque, mais lui est conféré par son effet sur la trajectoire de l'objet : il serait plus correct de parler de force à effet centripète
Pour assurer une telle compensation, cette force doit posséder des caractéristiques précises : elle doit être radiale, dirigée vers le centre de courbure, et son intensité doit être inversement proportionnelle au rayon de courbure de la trajectoire.
Sommaire
Formule de base
Le vecteur vitesse est défini par la vitesse et la direction du mouvement. Si la résultante (c'est-à-dire la somme des vecteurs) des forces appliquées à un objet est nulle, cet objet n'accélère pas et donc se déplace sur une ligne droite à vitesse constante : le vecteur vitesse est constant. Par contre, un objet qui se déplace à vitesse constante et dont la trajectoire est un cercle change en permanence de direction de mouvement. Le taux de variation du vecteur vitesse est alors appelé accélération centripète.
Cette accélération centripète
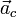 dépend du rayon r du cercle et de la vitesse v de l'objet. Plus la vitesse est grande, plus l'accélération augmente, de même plus le rayon est petit, plus elle augmente. De manière plus précise, l'accélération centripète est donnée par la formule
dépend du rayon r du cercle et de la vitesse v de l'objet. Plus la vitesse est grande, plus l'accélération augmente, de même plus le rayon est petit, plus elle augmente. De manière plus précise, l'accélération centripète est donnée par la formuleoù ω = v / r est la vitesse angulaire. Le signe négatif indique que la direction de cette accélération est dirigée vers le centre du cercle, c'est-à-dire opposée au vecteur position
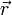 . (On suppose que l'origine de
. (On suppose que l'origine de 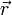 est placée au centre du cercle.)
est placée au centre du cercle.) 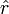 désigne le vecteur unitaire dans la direction de
désigne le vecteur unitaire dans la direction de 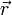 .
.D'après la Seconde loi de Newton,
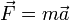 , la force physique
, la force physique 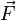 doit être appliquée à une masse m pour produire une telle accélération. La quantité de force nécessaire pour se déplacer à la vitesse v sur le cercle de rayon r est:
doit être appliquée à une masse m pour produire une telle accélération. La quantité de force nécessaire pour se déplacer à la vitesse v sur le cercle de rayon r est:l'expression ayant été formulée de différentes manières équivalentes. Ici,
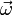 est le vecteur de vitesse angulaire. Ici encore, le signe négatif indique que la direction est dirigée vers l'intérieur vers le centre du cercle et dans la direction opposée au vecteur rayon
est le vecteur de vitesse angulaire. Ici encore, le signe négatif indique que la direction est dirigée vers l'intérieur vers le centre du cercle et dans la direction opposée au vecteur rayon 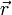 . Si la force appliquée est moins forte respectivement plus forte que
. Si la force appliquée est moins forte respectivement plus forte que 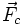 , l'objet va glisser vers l'extérieur respectivement l'intérieur, se déplaçant sur un cercle plus grand, resp. plus petit.
, l'objet va glisser vers l'extérieur respectivement l'intérieur, se déplaçant sur un cercle plus grand, resp. plus petit.Si un objet se déplace sur un cercle à une vitesse variable, son accélération peut être divisée en deux composantes : l'accélération radiale (l'accélération centripète) qui change la direction de la vitesse et une composante tangentielle qui change l'amplitude de la vitesse.
Exemples
Pour un satellite en orbite autour d'une planète, la force centripète est fournie par l'attraction gravitationnelle entre le satellite et la planète et elle agit en direction du barycentre des deux objets.
Pour un objet accroché au bout d'une corde et tournant autour d'un axe de rotation vertical, la force centripète est la composante horizontale de la tension de la corde qui agit en direction du barycentre entre l'axe de rotation et l'objet.
Pour un objet en mouvement circulaire uniforme, cette force vaut
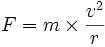 . v étant la vitesse et r, le rayon du cercle.
. v étant la vitesse et r, le rayon du cercle.Exemple numérique
Exemple : une balle de 1kg va à 2m·s-1 à une distance de 0,5m du poteau central, donc
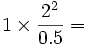 une force de 8 newtons (0,8 kgf)
une force de 8 newtons (0,8 kgf)où la conversion en kilogramme-force s'exprime comme suit :
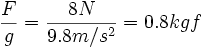 .
.Confusions usuelles
La force centripète ne doit pas être confondue avec la force centrifuge. Cette dernière est une force fictive qui surgit quand on est sur un référentiel en rotation. Pour éliminer toutes ces forces d'inerties, il faut être dans un référentiel non-accéléré, c'est-à-dire un référentiel galiléen qui permet alors d'utiliser les lois de Newton.
La force centripète ne doit pas non plus être confondue avec la force centrale. Les forces centrales sont une classe de forces physiques entre deux objets qui suivent deux conditions :
- la magnitude ne dépend que de la distance entre les deux objets
- la direction pointe le long de la ligne reliant les centres de ces deux objets.
Par exemple, la force gravitationnelle entre deux masses ou la force électrostatique entre deux charges électriques sont des forces centrales. La force centripète maintenant un objet en mouvement circulaire est souvent une force centrale.
Dérivation géométrique
 Les vecteurs position et vitesse se déplacent tout deux le long d'un cercle.
Les vecteurs position et vitesse se déplacent tout deux le long d'un cercle.Le cercle de gauche montre un objet se déplaçant sur un cercle à vitesse constante à quatre instants différents sur l'orbite. Son vecteur position est
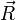 et son vecteur vitesse
et son vecteur vitesse  .
.Le vecteur vitesse
 est toujours perpendiculaire au vecteur position
est toujours perpendiculaire au vecteur position 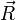 (car
(car  est toujours tangent au cercle) ; ainsi, comme
est toujours tangent au cercle) ; ainsi, comme 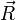 se déplace en cercle,
se déplace en cercle,  fait de même. Le mouvement circulaire de la vitesse est indiqué sur le dessin de droite, avec le mouvement de l'accélération
fait de même. Le mouvement circulaire de la vitesse est indiqué sur le dessin de droite, avec le mouvement de l'accélération 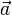 . La vitesse est le taux de variation de la position, l'accélération est le taux de variation de la vitesse.
. La vitesse est le taux de variation de la position, l'accélération est le taux de variation de la vitesse.Comme les vecteurs position et vitesse se déplacent conjointement, ils tournent autour de leurs cercles respectifs au même instant T. Ce temps est la distance parcourue divisée par la vitesse :
et par analogie,
En égalant ces deux équations et en résolvant pour a, on obtient:
la comparaison des deux cercles indique que l'accélération pointe vers le centre du cercle R. Par exemple, à un instant donné, le vecteur position
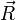 pointe vers 12 heures, le vecteur vitesse
pointe vers 12 heures, le vecteur vitesse  pointe vers 9 heures qui (en regardant sur le cercle de droite) a un vecteur d'accélération pointant vers 6 heures. Ainsi le vecteur accélération est opposé au vecteur position et pointe en direction du centre du cercle.
pointe vers 9 heures qui (en regardant sur le cercle de droite) a un vecteur d'accélération pointant vers 6 heures. Ainsi le vecteur accélération est opposé au vecteur position et pointe en direction du centre du cercle.Dérivation par l'analyse
Une autre stratégie de dérivation est d'utiliser un système de coordonnées polaires, en supposant que le rayon reste constant, et de dériver deux fois.
Soit
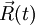 le vecteur décrivant la position d'une masse à un instant t. Comme on suppose que le mouvement est circulaire uniforme, on a
le vecteur décrivant la position d'une masse à un instant t. Comme on suppose que le mouvement est circulaire uniforme, on a 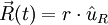 où r est constant (rayon du cercle) et
où r est constant (rayon du cercle) et 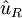 est le vecteur unitaire pointant depuis l'origine vers la masse. La direction est décrite par θ, angle entre l'axe des abscisses (x) et le vecteur unitaire, mesuré dans le sens trigonométrique (sens contraire des aiguilles d'une montre). Exprimé dans le système des coordonnées cartésiennes en utilisant les vecteurs unitaires
est le vecteur unitaire pointant depuis l'origine vers la masse. La direction est décrite par θ, angle entre l'axe des abscisses (x) et le vecteur unitaire, mesuré dans le sens trigonométrique (sens contraire des aiguilles d'une montre). Exprimé dans le système des coordonnées cartésiennes en utilisant les vecteurs unitaires 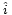 (axe des abscisses, x) et
(axe des abscisses, x) et 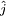 (axe des ordonnées, y), on a
(axe des ordonnées, y), on aNote: Contrairement aux vecteurs unités cartésiens, qui sont constants, la direction du vecteur unité en coordonnées polaires dépend de l'angle θ, et donc ses dérivées dépendent du temps.
En dérivant pour obtenir le vecteur vitesse :
où ω est la vitesse angulaire dθ/dt, et
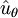 est le vecteur unitaire qui est perpendiculaire à
est le vecteur unitaire qui est perpendiculaire à 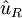 et qui pointe dans la direction des θ augmentant. En coordonnées cartésiennes, on a
et qui pointe dans la direction des θ augmentant. En coordonnées cartésiennes, on a 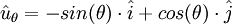 .
.Ce résultat indique que le vecteur vitesse est dirigé autour du cercle et en re-dérivant on obtient l'accélération
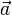
Et ainsi, la composante radiale de l'accélération est :
- aR = −ω2r
Références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Centripetal force ».
- Portail de la physique
Catégorie : Mécanique classique
Wikimedia Foundation. 2010.