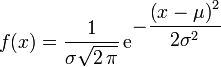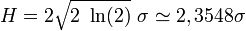Fonctions gaussiennes

Fonctions gaussiennes

Fonction gaussienne

Une fonction gaussienne est une fonction en exponentielle de l'opposé du carré de l'abscisse (une fonction en exp(-(x2)). Elle a une forme caractéristique de courbe en cloche.

L'exemple le plus connu est la densité de probabilité de la loi normale

f(x) = \frac{1}{\sigma \sqrt{2\,\pi}}\, \mathrm{e}^{\displaystyle-\frac{\left(x-\mu\right)^2}{2\sigma^2}}

où μ est l'espérance mathématique et σ est l'écart type.

La largeur à mi-hauteur (FWHM, full width at half maximum) H vaut

H = 2 \sqrt{2\ \ln(2)}\ \sigma \simeq 2,3548 \sigma

la demi largeur à mi-hauteur vaut donc environ 1,178·σ.

Il ne faut pas confondre ces fonctions avec la « fonction de Gauss », également appelée fonction d'erreur erf.

Fonction gaussienne pour μ = 0, σ = 1 Courbe centrée en zéro

Application

Les fonctions gaussiennes sont très utilisées en physique. En effet, nombre de phénomènes physiques suivent une distribution de type gaussien, à cause du théorème de la limite centrale. L'intérêt des fonctions gaussiennes en physique est également dû à certaines de leurs propriétés mathématiques remarquables. Par exemple, la transformée de Fourier d'une fonction gaussienne est une fonction gaussienne, ce qui entraine notamment le fait que les faisceaux lasers sont des faisceaux gaussiens.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Fonction gaussienne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonctions gaussiennes de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Liste de fonctions numériques — En mathématiques, certaines fonctions ont une dénomination usuelle, dépendant éventuellement d un ou plusieurs paramètres numériques, qui les définit précisément. Il peut s agir de fonctions d une ou plusieurs variables réelles ou complexes,… …   Wikipédia en Français

  • Base (Chimie Quantique) — Pour les articles homonymes, voir Base. Une base en chimie quantique est un ensemble de fonctions utilisées afin de créer des orbitales moléculaires, qui sont développées comme combinaisons linéaires de telles fonctions avec des poids ou… …   Wikipédia en Français

  • Base (chimie quantique) — Pour les articles homonymes, voir Base. Une base en chimie quantique est un ensemble de fonctions utilisées afin de modéliser des orbitales moléculaires, qui sont développées comme combinaisons linéaires de telles fonctions avec des poids ou… …   Wikipédia en Français

  • Orbitale de type gaussien — En chimie numérique, les orbitales de type gaussien (connues aussi comme orbitales gaussiennes ou gaussiennes, en anglais Gaussian orbitals GTO) sont des fonctions utilisées comme orbitales atomiques dans les méthodes LCAO pour le calcul des… …   Wikipédia en Français

  • Orbitale gaussienne — Orbitale de type gaussien En chimie numérique, les orbitales de type gaussien (connues aussi comme orbitales gaussiennes ou gaussiennes, en anglais Gaussian orbitals GTO) sont des fonctions utilisées comme orbitales atomiques dans les méthodes… …   Wikipédia en Français

  • Base STO-nG — Une base STO nG est une base utilisée en chimie numérique, c est à dire un ensemble de fonctions utilisées afin de créer des orbitales moléculaires. Il s agit d une base minimale pour laquelle n orbitales gaussiennes primitives sont ajustées à… …   Wikipédia en Français

  • Equipartition de l'énergie — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… …   Wikipédia en Français

  • Theoreme d'equipartition — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… …   Wikipédia en Français

  • Théorème d'équipartition — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… …   Wikipédia en Français

  • Théorème d’équipartition — Équipartition de l énergie Agitation thermique d’un peptide avec une structure en hélice alpha. Les mouvements sont aléatoires et complexes, l’énergie d’un atome peut fluctuer énormément. Néanmoins, le théorème d’équipartition permet de calculer… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”