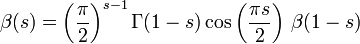Fonction zeta de Catalan

Fonction bêta de Dirichlet

En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C'est un cas particulier de fonction L de Dirichlet pour le caractère de Dirichlet alterné de période 4.

Elle est définie comme la fonction d'une variable complexe s, pour s de partie réelle plus grande que 1, par la série :

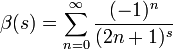$\beta(s)=\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^s}$ ,

ou par l'intégrale

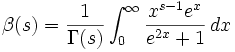$\beta(s) = \frac{1}{\Gamma(s)}\int_0^{\infty}\frac{x^{s-1}e^x}{e^{2x} + 1}\,dx$ .

Dans ces deux cas, les deux formules ne sont valables que pour Re(s)>0.

Autrement, on peut définir la fonction bêta de Dirichlet par la fonction zêta d'Hurwitz, qui est valable pour tous nombres complexes:

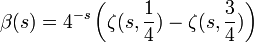$\beta(s) = 4^{-s} \left( \zeta(s,{{1} \over {4}})-\zeta(s, {{3} \over {4}}) \right)$ .

Ou par une autre définition équivalente, du point de vue de la fonction transcendante de Lerch:

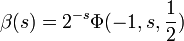$\beta(s) = 2^{-s} \Phi(-1,s,{{1} \over {2}})$ ,

qui est aussi valable pour tous nombres complexes.

Cette fonction se prolonge de façon méromorphe sur le plan complexe.

Équation fonctionnelle

L'équation fonctionnelle suivante permet d'étendre la fonction β à la partie gauche du plan complexe Re(s) <1.

$\beta(s)=\left(\frac{\pi}{2}\right)^{s-1} \Gamma(1-s) \cos \left(\frac{\pi s}{2}\right)\,\beta(1-s)$

où Γ(s) est la fonction gamma d'Euler.

Valeurs spéciales

On peut noter les valeurs particulières suivantes :

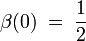$\beta(0)\;=\;\frac{1}{2}$ ,
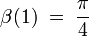$\beta(1)\;=\;\frac{\pi}{4}$ ,
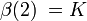$\beta(2)\;=K$ , où K est la constante de Catalan.
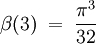$\beta(3)\;=\;\frac{\pi^3}{32}$ .
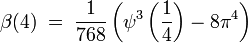$\beta(4)\;=\;\frac{1}{768}\left(\psi^3\left(\frac{1}{4}\right)-8\pi^4\right)$ ,
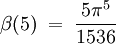$\beta(5)\;=\;\frac{5\pi^5}{1536}$ ,
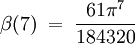$\beta(7)\;=\;\frac{61\pi^7}{184320}$ ,

où $ψ 3 (1 / 4)$ est la fonction polygamma de troisième ordre de 1/4.

Plus généralement, les valeurs prises par la fonction β aux entiers positifs impairs sont des multiples rationnels de puissances de π.

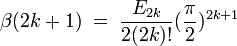$\beta(2k+1)\;=\;\frac{E_{2k}}{2(2k)!}(\frac{\pi}{2})^{2k+1}$ ,

ou les $E 2 k$ sont des nombres d'Euler. Et les valeurs de la fonction bêta de Dirichlet des entiers pairs négatifs sont données aussi par les nombres d'Euler avec:

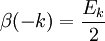$\beta(-k)={{E_{k}} \over {2}}$ .

Par contre, on ne connaît pas grand chose sur les valeurs aux entiers positifs pairs. Le nombre $β(2)$ est appelé la constante de Catalan.

Voir aussi

Références

J. Spanier and K. B. Oldham, An Atlas of Functions, (1987) Hemisphere, New York.

Portail des mathématiques

Ce document provient de « Fonction b%C3%AAta de Dirichlet ».

Catégorie : Fonction zêta

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction zeta de Catalan de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Fonction zêta de Catalan — Fonction bêta de Dirichlet En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas particulier de fonction L de… … Wikipédia en Français
Fonction Beta De Dirichlet — Fonction bêta de Dirichlet En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas particulier de fonction L de… … Wikipédia en Français
Fonction beta de Dirichlet — Fonction bêta de Dirichlet En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas particulier de fonction L de… … Wikipédia en Français
Fonction beta de dirichlet — Fonction bêta de Dirichlet En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas particulier de fonction L de… … Wikipédia en Français
Fonction β de Dirichlet — Fonction bêta de Dirichlet En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas particulier de fonction L de… … Wikipédia en Français
Fonction De Clausen — En mathématiques, la fonction de Clausen est définie par l intégrale suivante : Plus généralement, on définit . Elle est reliée au polylogarithme par . Ernst Kummer e … Wikipédia en Français
Fonction de clausen — En mathématiques, la fonction de Clausen est définie par l intégrale suivante : Plus généralement, on définit . Elle est reliée au polylogarithme par . Ernst Kummer e … Wikipédia en Français
Fonction bêta de Dirichlet — Ne pas confondre avec la fonction bêta à deux variables. En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas… … Wikipédia en Français
Fonction de Clausen — En mathématiques, la fonction de Clausen est définie par l intégrale suivante : Plus généralement, on définit . Elle est reliée au polylogarithme par . Ernst Kummer et Rogers donnent la relation … Wikipédia en Français
Constante de Catalan — En mathématiques, la constante de Catalan, nommée d après le mathématicien Eugène Charles Catalan, est le nombre défini par : [1] où β est la fonction beta de Dirichlet. On ne sait pas si la constante K est rationnelle ou irrationnelle mais… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction zeta de Catalan

Fonction bêta de Dirichlet

Sommaire

Équation fonctionnelle

Valeurs spéciales

Voir aussi

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Fonction zeta de Catalan

Fonction bêta de Dirichlet

Sommaire

Équation fonctionnelle

Valeurs spéciales

Voir aussi

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link