Fonction digamma
- Fonction digamma
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Fonction digamma de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
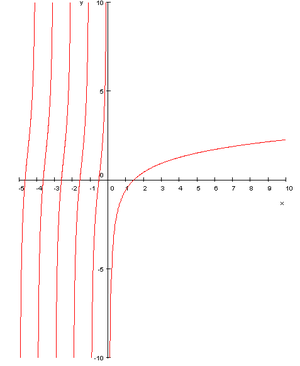
Fonction Digamma — Représentation de la fonction digamma ψ(s) sur la droite des réels. En mathématiques, la fonction digamma ou fonction psi est définie par où D … Wikipédia en Français
Fonction Polygamma — Tracé de la fonction polygamma le long de l axe des réels avec en orange m=0, en jaune m=1, en vert m=2, en rouge m=3 et en bleu m=4 En mathématiques, la fonction polygamma d ordre m est définie comme la m+1 ième dérivée logarithmique de la… … Wikipédia en Français
Fonction Gamma — Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction g … Wikipédia en Français
Fonction Gamma d'Euler — Fonction gamma Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction g … Wikipédia en Français
Fonction polygamma — Tracé de la fonction polygamma le long de l axe des réels avec en orange m=0, en jaune m=1, en vert m=2, en rouge m=3 et en bleu m=4 En mathématiques, la fonction polygamma d ordre m est définie comme la m+1 ième dérivée logarithmique de la… … Wikipédia en Français
Fonction gamma — Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction gamma (ou fonction Gamma) est une fonction … Wikipédia en Français
Fonction spéciale — Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques non élémentaires[1] … Wikipédia en Français
Fonctions Spéciales — Fonction spéciale Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques… … Wikipédia en Français
Fonctions speciales — Fonction spéciale Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques… … Wikipédia en Français
Fonctions spéciales — Fonction spéciale Interférences d ondes émises par deux sources cylindriques. Le phénomène s interprète à l aide des fonctions de Bessel. L analyse mathématique regroupe sous le terme de fonctions spéciales un ensemble de fonctions analytiques… … Wikipédia en Français
Représentation de la fonction digamma ψ(s) sur la droite des réels.
ou même 
, est reliée aux nombres harmoniques par
est le (n - 1)-ième nombre harmonique, et 
est la célèbre constante d'Euler-Mascheroni.
![\psi\left(\frac{1}{8}\right) = -\frac{\pi}{2} - 4\ln(2) - \frac{\sqrt{2}}{2} \left[\pi + \ln\left(2 + \sqrt{2}\right) - \ln\left(2 - \sqrt{2}\right)\right] - \gamma](5/9b57e9b970dc0bf7090330435f5875d0.png)
