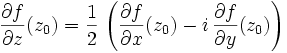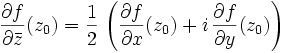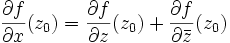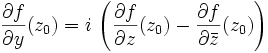- Fonction d'une variable complexe differentiable au sens reel
-
Fonction d'une variable complexe différentiable au sens réel
Cet article constitue essentiellement une introduction à l'article sur les équations de Cauchy-Riemann qu'il permet d'aborder directement. Il définit, pour les fonctions d'une variable complexe et à valeurs complexes : les dérivées partielles (par rapport à
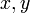 ou
ou 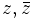 ) et la différentiabilité au sens réel.
) et la différentiabilité au sens réel.
On considère une fonction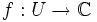 d'une variable complexe, définie sur un sous-ensemble ouvert U du plan complexe
d'une variable complexe, définie sur un sous-ensemble ouvert U du plan complexe 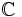 . On utilisera les notations suivantes :
. On utilisera les notations suivantes :- la variable complexe
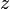 sera notée
sera notée 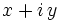 , où x, y sont réels
, où x, y sont réels - les parties réelle et imaginaire de
 seront notées respectivement
seront notées respectivement 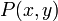 et
et 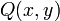 , c'est-à-dire :
, c'est-à-dire :  , où
, où 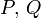 sont deux fonctions réelles de deux variables réelles.
sont deux fonctions réelles de deux variables réelles.
Sommaire
Dérivées partielles d'une fonction d'une variable complexe
Dérivées partielles par rapport à x et y
Définition : soit
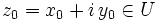 , où
, où 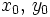 sont réels.
sont réels.- on dit que f admet une dérivée partielle (d'ordre 1) au point
 par rapport à la variable x, notée
par rapport à la variable x, notée 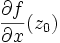 si la limite (finie)
si la limite (finie) 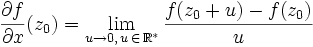 existe
existe - on dit que f admet une dérivée partielle (d'ordre 1) au point
 par rapport à la variable y, notée
par rapport à la variable y, notée 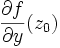 si la limite (finie)
si la limite (finie)  existe
existe
Propriété :- la dérivée partielle
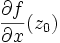 existe si et seulement si les dérivées partielles
existe si et seulement si les dérivées partielles  ,
, 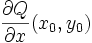 existent, et alors
existent, et alors 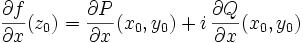
- la dérivée partielle
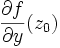 existe si et seulement si les dérivées partielles
existe si et seulement si les dérivées partielles 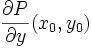 ,
, 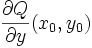 existent, et alors
existent, et alors 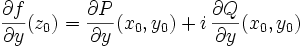
Dérivées partielles d'ordre supérieur :
- si, par exemple,
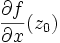 existe en tout point
existe en tout point 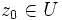 , on définit la fonction
, on définit la fonction 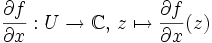
- si, de plus, la fonction
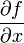 admet une dérivée partielle d'ordre 1 au point
admet une dérivée partielle d'ordre 1 au point  par rapport à la variable x, on la note
par rapport à la variable x, on la note 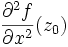 :
: 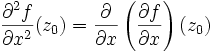 . De manière analogue, si
. De manière analogue, si 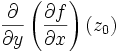 existe, on la note
existe, on la note  , etc.
, etc.
Dérivées partielles par rapport à
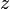 et
et 
Définition : on suppose que f admette des dérivées partielles d'ordre 1 par rapport à x et y au point
 . Alors, on définit :
. Alors, on définit :Propriété : en conservant les hypothèses précédentes
Différentiabilité au sens réel des fonctions d'une variable complexe
On dit qu'une fonction d'une variable complexe est différentiable au sens réel, ou
 -différentiable en un point si on peut l'approcher localement (au voisinage de ce point) par la somme d'une constante et d'une fonction
-différentiable en un point si on peut l'approcher localement (au voisinage de ce point) par la somme d'une constante et d'une fonction  -linéaire ; cette dernière est alors unique, et s'appelle différentielle de la fonction au point considéré.
-linéaire ; cette dernière est alors unique, et s'appelle différentielle de la fonction au point considéré.Plus précisément, cela veut dire que
 , en tant que fonction de deux variables réelles, admet au voisinage du point considéré un développement limité d'ordre 1, dont la différentielle est la partie linéaire.
, en tant que fonction de deux variables réelles, admet au voisinage du point considéré un développement limité d'ordre 1, dont la différentielle est la partie linéaire.- Définition : on dit qu'une application
 est
est  -linéaire si :
-linéaire si : 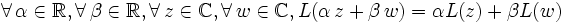 .
.
- (alors :
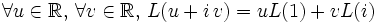 )
)
- (alors :
- Définition : on dit que la fonction
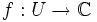 est
est  -différentiable en un point
-différentiable en un point 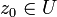 s'il existe une application
s'il existe une application  -linéaire
-linéaire  et une fonction
et une fonction  d'une variable complexe telles que
d'une variable complexe telles que  lorsque
lorsque 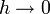 et
et 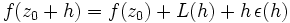 (en supposant que
(en supposant que 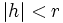 , où r est le rayon d'une boule ouverte telle que
, où r est le rayon d'une boule ouverte telle que 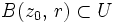 ).
).
- Lorsqu'elle existe, l'application L est unique (ceci résulte de la propriété suivante) ; on l'appelle
 -différentielle ou différentielle de
-différentielle ou différentielle de  en
en  et on la note habituellement
et on la note habituellement 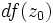 .
. - On dit que
 est
est  -différentiable sur U si elle est
-différentiable sur U si elle est  -différentiable en tout point de U.
-différentiable en tout point de U.
- Lorsqu'elle existe, l'application L est unique (ceci résulte de la propriété suivante) ; on l'appelle
- Propriété : si
 est
est  -différentiable en un point
-différentiable en un point 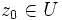 , alors
, alors
- elle est continue en

- elle admet des dérivées partielles d'ordre 1 en
 , et
, et 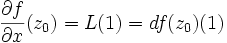 ,
, 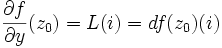 .
.
- elle est continue en
démonstration :
- continuité :
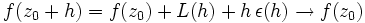 lorsque
lorsque 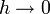 parce que
parce que 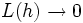 (la
(la  -différentielle L est un endomorphisme d'un espace vectoriel de dimension finie, donc elle est continue) et
-différentielle L est un endomorphisme d'un espace vectoriel de dimension finie, donc elle est continue) et 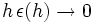 .
. - existence et expression des dérivées partielles d'ordre 1 :
- pour tout u réel tel que
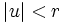 ,
, 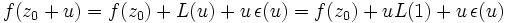 ; donc, si
; donc, si  ,
, 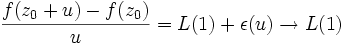 lorsque
lorsque 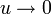 : ceci prouve l'existence de la dérivée partielle de la fonction
: ceci prouve l'existence de la dérivée partielle de la fonction  en
en  par rapport à
par rapport à 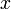 , et la relation
, et la relation 
- pour tout v réel tel que
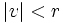 ,
, 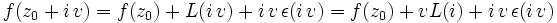 ; donc, si
; donc, si 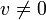 ,
, 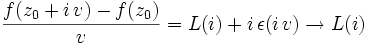 lorsque
lorsque 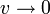 : ceci prouve l'existence de la dérivée partielle de la fonction
: ceci prouve l'existence de la dérivée partielle de la fonction  en
en  par rapport à
par rapport à  , et la relation
, et la relation 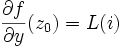 .
.
- pour tout u réel tel que
- Théorème : une condition suffisante (non nécessaire) de
 -différentiabilité en un point, ou sur un ouvert.
-différentiabilité en un point, ou sur un ouvert.
- Soit
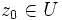 . Si
. Si  admet des dérivées partielles d'ordre 1 par rapport à x et y (ou à
admet des dérivées partielles d'ordre 1 par rapport à x et y (ou à 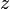 et
et 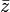 ) en tout point d'un voisinage de
) en tout point d'un voisinage de  , et si
, et si 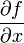 ,
, 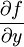 (ou
(ou 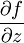 ,
, 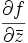 ) sont continues en
) sont continues en  , alors
, alors  est
est  -différentiable en
-différentiable en 
- En particulier, si
 admet des dérivées partielles d'ordre 1 par rapport à x et y (ou à
admet des dérivées partielles d'ordre 1 par rapport à x et y (ou à 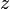 et
et 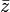 ) définies et continues en tout point de l'ouvert U, la fonction
) définies et continues en tout point de l'ouvert U, la fonction  est
est  -différentiable sur U. Dans ce cas, on dit que
-différentiable sur U. Dans ce cas, on dit que  est
est  -continûment différentiable sur U, ou de classe
-continûment différentiable sur U, ou de classe 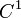 sur U.
sur U.
- Soit
Voir aussi
- Portail des mathématiques
Catégorie : Analyse complexe - la variable complexe
Wikimedia Foundation. 2010.