Flot Géodésique

Flot Géodésique

Flot géodésique

En mathématiques, le flot géodésique, parfois également appelé : « coulée géodésique », permet de décrire la dynamique classique d'une particule massive se déplaçant librement sur une variété riemannienne V. Il est formalisé par un groupe continu à un paramètre qui opère sur le fibré tangent unitaire T1V de la variété V.

Lorsque la variété V est compacte à courbure négative constante, le flot géodésique fournit à la physique théorique le modèle le plus simple de système hamiltonien complètement chaotique.

Sommaire

Description

Étant donné un point (x,v) du fibré tangent unitaire de V, soit 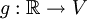g:\R \rightarrow V l'unique géodésique de V telle que g(0) = x et g'(0) = v parcourue à vitesse constante égale à 1.

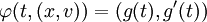
Le flot géodésique est alors défini par \varphi(t,(x,v))=(g(t),g'(t))

Exemples

Le flot géodésique des surfaces à courbure négative constante

Dès 1898, Hadamard reconnaissait que le flot géodésique sur une surface à courbure négative constante possédait une dynamique présentant la propriété de sensibilité aux conditions initiales, devenue depuis l'un des paradigme de la théorie du chaos.

Ce flot est une parfaite illustration des propriétés de la hiérarchie ergodique ; il est en effet, par ordre d' « instabilité » croissante :

  • mélangeant (Hedlung [3] & Hopf [4])
  • isomorphe à un système de Bernouilli (Ornstein & Weiss [6].)

Articles connexes

Bibliographie

  • Jacques Hadamard ; Les surfaces à courbures opposées et leurs lignes géodésiques, Journal de Mathématiques Pures & Appliquées 4 (1898) 27.
  • Yakov Pesin ; Geodesic Flows With Hyperbolic Behavior of The Trajectories and Objects Connected With Them, Russian Mathematical Surveys 36:4 (1981), 3--15.
  • Pierre Pansu ; Le flot géodésique des variétés Riemanniennes à courbure négative, Séminaire Bourbaki 738 (1991), publié dans : Astérisque 201-203 (1991), 269-298.

Bibliothèque virtuelle

  • Mark Pollicott ; Lectures on ergodic theory, geodesic flows and related topics, Ulm (2003). Notes de cours non corrigées disponibles en pdf.
  • Mark Pollicott ; Dynamical zeta functions and closed orbits for geodesic and hyperbolic flows, Les Houches (2003). Notes de cours non corrigées disponibles en pdf.

Notes

  1. ↑ G. Hedlung ; On the metrical transitivity of the geodesics on closed surfaces of constant negative curvature, Annals of Mathematics 35 (1935), 787-808.
  2. ↑ E. Hopf ; Ergodentheorie, Springer (1937).
  3. ↑ G. Hedlung ; The dynamics of geodesic flows, Bulletin of the American Mathematical Society 35 (1939), 241-246.
  4. ↑ E. Hopf ; Statistik der geodätischen linien in mannigfaltigkeiten negativer krümung, Berichte uber die Verhandlungen der Sächsischen, Akademie der Wissenschaften Leipzig 91 (1939), 261-304.
  5. ↑ D. Anosov ; Geodesic flows on compact Riemannian manifolds of negative curvature, Proceedings of the Steklov Mathematical Institute 90:1 (1967), 1-235.
  6. ↑ D. Ornstein & B. Weiss ; Geodesic flows are Bernouillian, Israel Journal of Mathematics 14 (1973), 184.
  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Flot g%C3%A9od%C3%A9sique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Flot Géodésique de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Flot geodesique — Flot géodésique En mathématiques, le flot géodésique, parfois également appelé : « coulée géodésique », permet de décrire la dynamique classique d une particule massive se déplaçant librement sur une variété riemannienne V. Il est… …   Wikipédia en Français

  • Flot géodésique — En mathématiques, le flot géodésique, parfois également appelé : « coulée géodésique », permet de décrire la dynamique classique d une particule massive se déplaçant librement sur une variété riemannienne V. Il est formalisé par un …   Wikipédia en Français

  • SYSTÈMES DYNAMIQUES DIFFÉRENTIABLES — Sans doute née avec le mémoire que Poincaré écrivit en 1881 «sur les courbes définies par des équations différentielles», où l’étude quantitative (analytique) locale des équations différentielles dans le champ complexe est remplacée par leur… …   Encyclopédie Universelle

  • Theorie ergodique — Théorie ergodique La théorie ergodique est une branche des mathématiques née de l étude de l hypothèse ergodique formulée par le physicien Ludwig Boltzmann en 1871 pour sa théorie cinétique des gaz. Elle a connu de nombreux développements en… …   Wikipédia en Français

  • Théorie ergodique — La théorie ergodique est une branche des mathématiques née de l étude de l hypothèse ergodique formulée par le physicien Ludwig Boltzmann en 1871 pour sa théorie cinétique des gaz. Elle a connu de nombreux développements en relation étroite avec… …   Wikipédia en Français

  • Chaotique — Théorie du chaos Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des sys …   Wikipédia en Français

  • Theorie du chaos — Théorie du chaos Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des sys …   Wikipédia en Français

  • Théorie du Chaos — Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des sys …   Wikipédia en Français

  • Théorie du chaos — Pour les articles homonymes, voir Chaos. Attracteur étrange de Lorenz La théorie du chaos traite des systèmes dynamiques rigoureusement déterminis …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”