Flot Anosov
- Flot Anosov
-
Flot d'Anosov
En systèmes dynamiques et en géométrie différentielle, un flot Anosov est un flot différentiable, analogue en dynamique continue des difféomorphismes hyperboliques, et qui, comme ces derniers, présente des résultats de stabilité structurelle et de régularité remarquables.
Sur une variété différentielle compacte N, un groupe à un paramètre de difféomorphismes Φt s'obtient par intégration d'un champ de vecteurs R :
![\frac{d}{dt} \Phi_t(x)=R\left[\Phi_t(x)\right]](/pictures/frwiki/57/937dc878825e6c7e57a3e32db0b4359f.png)
La distribution en droites Eo est intégrable, et les feuilles de la distribution correspondante sont les orbites de Φt. Le flot Φt de classe C1 est appelé flot Anosov lorsqu'il ne possède aucun point fixe, et que de plus il existe des distributions Es et Eo et des constantes C,0 < λ < 1 telles que :
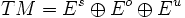
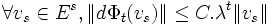
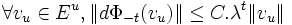
Hyperbolicité
Régularité
Stabilité structurelle
Catégories : Système dynamique remarquable | Géométrie riemannienne
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Flot Anosov de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Flot anosov — Flot d Anosov En systèmes dynamiques et en géométrie différentielle, un flot Anosov est un flot différentiable, analogue en dynamique continue des difféomorphismes hyperboliques, et qui, comme ces derniers, présente des résultats de stabilité… … Wikipédia en Français
Flot d'Anosov — En systèmes dynamiques et en géométrie différentielle, un flot Anosov est un flot différentiable, analogue en dynamique continue des difféomorphismes hyperboliques, et qui, comme ces derniers, présente des résultats de stabilité structurelle et… … Wikipédia en Français
Flot Géodésique — En mathématiques, le flot géodésique, parfois également appelé : « coulée géodésique », permet de décrire la dynamique classique d une particule massive se déplaçant librement sur une variété riemannienne V. Il est formalisé par un … Wikipédia en Français
Flot geodesique — Flot géodésique En mathématiques, le flot géodésique, parfois également appelé : « coulée géodésique », permet de décrire la dynamique classique d une particule massive se déplaçant librement sur une variété riemannienne V. Il est… … Wikipédia en Français
Flot géodésique — En mathématiques, le flot géodésique, parfois également appelé : « coulée géodésique », permet de décrire la dynamique classique d une particule massive se déplaçant librement sur une variété riemannienne V. Il est formalisé par un … Wikipédia en Français
Systeme d'Anosov — Système d Anosov Pour consulter un article plus général, voir : théorie du chaos. En théorie des systèmes dynamiques, un système d Anosov est un système hyperbolique, qui présente une dynamique extrèmement chaotique. Sommaire 1 Définition… … Wikipédia en Français
Système d'Anosov — Pour consulter un article plus général, voir : théorie du chaos. En théorie des systèmes dynamiques, un système d Anosov est un système hyperbolique, qui présente une dynamique extrêmement chaotique. Sommaire 1 Définition 1.1 Notion de… … Wikipédia en Français
Dmitri Anosov — Dmitri Viktorovich Anosov (Moscou, 1936 ), mathématicien russe. « Master » du Département de mécanique et de mathématiques de l Université d État de Moscou en 1958. Il y est élève de Pontryagin alors que celui ci vient juste d… … Wikipédia en Français
Courbure Négative — Une variété riemannienne (M,g) est dite à courbure négative lorsque sa courbure sectionnelle est strictement négative. Les propriétés de ces variétés sont remarquables : Toute surface compacte orientable admet une métrique riemannienne de… … Wikipédia en Français
Courbure negative — Courbure négative Une variété riemannienne (M,g) est dite à courbure négative lorsque sa courbure sectionnelle est strictement négative. Les propriétés de ces variétés sont remarquables : Toute surface compacte orientable admet une métrique… … Wikipédia en Français
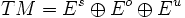
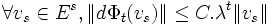
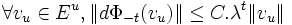

![\frac{d}{dt} \Phi_t(x)=R\left[\Phi_t(x)\right]](/pictures/frwiki/57/937dc878825e6c7e57a3e32db0b4359f.png)