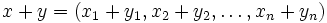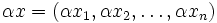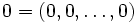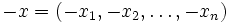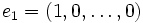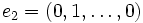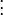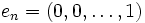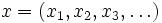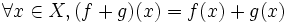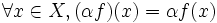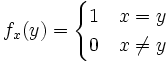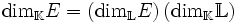Exemples D'espaces Vectoriels

Exemples d'espaces vectoriels

Cette page présente une liste d'exemples d'espaces vectoriels. Vous pouvez consulter l'article espace vectoriel pour y trouver les définitions des notions employées ci-dessous.

Voyez également les articles sur la dimension, les bases.

Nous noterons $\mathbb{K}$ un corps commutatif arbitraire tel que celui des réels $\mathbb{R}$ ou celui des complexes $\mathbb{C}$ .

Sommaire

1 Espace vectoriel trivial ou nul
2 Le corps
3 Espace des n-uplets
4 Espace des suites à support fini
5 Matrices
6 Espace vectoriel des polynômes
- 6.1 à un indéterminée
- 6.2 à plusieurs indéterminées
7 Espaces fonctionnels
8 Extensions de corps
9 Espaces vectoriels finis

Espace vectoriel trivial ou nul

Article détaillé : espace nul.

L'exemple le plus simple d'espace vectoriel est l'espace nul ${0}$ , qui ne contient que le vecteur nul (voir l'axiome 3. des espaces vectoriels). L'addition vectorielle et la multiplication par un scalaire sont triviales. Une base de cet espace vectoriel est l'ensemble vide, ainsi {0} est l'espace vectoriel de dimension 0 sur $\mathbb{K}$ . Tout espace vectoriel sur $\mathbb{K}$ contient un sous-espace vectoriel isomorphe à celui-ci.

Le corps

Le prochain exemple simple est le corps $\mathbb{K}$ lui-même. L'addition vectorielle est simplement l'addition du corps et la multiplication par un scalaire est la multiplication du corps. L'élément neutre de $\mathbb{K}$ pour la multiplication forme une base de $\mathbb{K}$ et ainsi $\mathbb{K}$ est un espace vectoriel de dimension 1 sur lui-même.

$\mathbb{K}$ a seulement deux sous-espaces { 0 } et $\mathbb{K}$ lui-même.

Espace des n-uplets

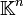L'exemple le plus important d'espace vectoriel est sans doute celui qui suit. Pour tout entier naturel strictement positif $n$ , l'ensemble des $n$ -uplets d'éléments de $\mathbb{K}$ forme un espace vectoriel de dimension $n$ sur $\mathbb{K}$ appelé l'espace des n-uplets, noté $\mathbb{K}^n$ . Un élément de 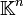$\mathbb{K}^n$ s'écrit:

$x = (x_1, x_2, \ldots, x_n) \,$

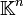où chaque $x i$ est un élément de $\mathbb{K}$ . Les opérations sur $\mathbb{K}^n$ sont définies par:

$x + y = (x_1 + y_1, x_2 + y_2, \ldots, x_n + y_n) \,$

$\alpha x = (\alpha x_1, \alpha x_2, \ldots, \alpha x_n) \,$

L'élément neutre pour l'addition est :

$0 = (0, 0, \ldots, 0) \,$

et l'opposé d'un élément : 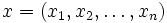$x = (x_1, x_2, \ldots, x_n) \,$ est le vecteur

$-x = (-x_1, -x_2, \ldots, -x_n) \,$

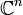Les cas les plus fréquents sont ceux où $\mathbb{K}$ est ou bien le corps des nombres réels donnant l'espace euclidien $\mathbb{R}^n$ , ou bien le corps des nombres complexes donnant $\mathbb{C}^n$ .

Les ensembles des quaternions et des octonions sont respectivement des espaces vectoriels de dimension quatre et huit sur le corps des nombres réels.

L'espace vectoriel 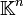$\mathbb{K}^n$ est généralement muni d'une base naturelle appelée base canonique:

$e_1 = (1, 0, \ldots, 0) \,$

$e_2 = (0, 1, \ldots, 0) \,$

$\vdots \,$

$e_n = (0, 0, \ldots, 1) \,$

où 1 désigne l'élément neutre multiplicatif de $\mathbb{K}$ .

Espace des suites à support fini

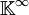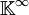Soit $\mathbb{K}^{\infty}$ l'ensemble des suites infinies d'éléments de $\mathbb{K}$ telles que seul un nombre fini d'éléments soit non nul. Plus précisément, si nous écrivons un élément de $\mathbb{K}^{\infty}$ sous la forme:

$x = (x_1, x_2, x_3, \ldots) \,$

alors seulement un nombre fini des nombres $x i$ est non nul (autrement dit les coordonnées du vecteur $x$ deviennent nulles à partir d'un certain rang).

L'addition et la multiplication par un scalaire sont alors définies comme sur l'espace vectoriel des $n$ -uplets.

L'ensemble 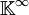$\mathbb{K}^{\infty}$ est un espace vectoriel de dimension infinie dénombrable. La base canonique est celle formée par les vecteurs 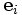$\textbf{e}_i$ qui comportent un 1 à la $i$ ème place et des zéros partout ailleurs.

Cet espace vectoriel est le coproduit d'un nombre dénombrable de copies de l'espace vectoriel $\mathbb{K}$ .

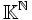Remarquez le rôle de la condition de finitude ici. Nous pourrions considérer des suites arbitraires d'élements de $\mathbb{K}$ , qui constituent aussi un espace vectoriel (souvent noté $\mathbb{K}^{\mathbb{N}}$ ).

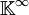Cependant la dimension de cet espace est infinie non dénombrable et il n'y a pas de choix évident de bases. Puisque les dimensions sont distinctes, l'espace vectoriel des suites de $\mathbb{K}$ n'est pas isomorphe à $\mathbb{K}^{\infty}$ . Cet espace vectoriel est le produit d'un nombre dénombrable de copies de $\mathbb{K}$ .

Il vaut la peine de noter que 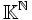$\mathbb{K}^{\mathbb{N}}$ est l'espace dual de 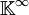$\mathbb{K}^{\infty}$ . Ainsi, dans la comparaison au cas rigide de la dimension finie, nous voyons qu'un espace vectoriel de dimension infinie n'a nul besoin d'être isomorphe à son dual (et encore moins d'être isomorphe à son bidual).

Matrices

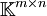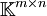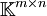Soit $\mathbb{K}^{m\times n}$ l'ensemble des matrices à coefficients dans $\mathbb{K}$ . Alors $\mathbb{K}^{m\times n}$ muni de l'addition des matrices et la multiplication par un scalaire des matrices (consistant à multiplier chaque coefficient par un même scalaire) est un espace vectoriel sur $\mathbb{K}$ . Le vecteur nul n'est autre que la matrice nulle. La dimension de $\mathbb{K}^{m\times n}$ est égale à $m n$ .

La base canonique est la base formée par les matrices ayant un seul coefficient égal à 1 et tous les autres coefficients égaux à 0.

Espace vectoriel des polynômes

à un indéterminée

L'ensemble des polynômes à coefficients dans $\mathbb{K}$ est un espace vectoriel sur $\mathbb{K}$ noté $\mathbb{K}[X]$ . L'addition vectorielle et la multiplication par un scalaire sont définies de manière évidente. Cet espace est de dimension infinie dénombrable. Si l'on ne garde que les polynômes dont le degré reste inférieur ou égal à $n$ alors nous obtenons l'espace vectoriel $\mathbb{K}_n[X]$ qui est de dimension $n + 1$ .

La base canonique de cet espace est une base monomiale.

à plusieurs indéterminées

L'ensemble des polynômes à plusieurs indéterminées à coefficients dans $\mathbb{K}$ est un espace vectoriel sur $\mathbb{K}$ noté $\mathbb{K}[X_1, X_2, \ldots, X_n]$ . Ici $n$ est un entier naturel non nul représentant le nombre d'indéterminées.

Voyez aussi: l'anneau des polynômes

Espaces fonctionnels

Voyez l'article principal à la page espace fonctionnel, et plus particulièrement la section intitulée analyse fonctionnelle.

Soit $X$ un ensemble quelconque et $E$ un espace vectoriel arbitraire sur $\mathbb{K}$ . L'ensemble de toutes les applications de $X$ dans $E$ est un espace vectoriel sur $\mathbb{K}$ avec l'addition et la multiplication par un scalaire des fonctions.

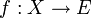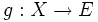Ces lois sont définies de la manière suivante: considérons $f:X\rightarrow E$ et $g:X\rightarrow E$ deux fonctions, et 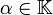$\alpha\in\mathbb{K}$ on a

$\forall x\in X, (f + g)(x) = f(x) + g(x) \,$

$\forall x\in X, (\alpha f)(x) = \alpha f(x) \,$

où les lois $+$ et $.$ apparaissant dans le second membre sont celle de $E$ . Le vecteur nul est la fonction constante nulle envoyant tout les éléments de $X$ sur le vecteur nul de $E$ .

Si $X$ est fini et $E$ est un espace vectoriel de dimension finie alors l'espace vectoriel des fonctions de $X$ dans $E$ est de dimension 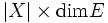$|X|\times {\rm dim }E$ , sinon l'espace vectoriel est de dimension infinie (non dénombrable si $X$ est infini).

Beaucoup d'espaces vectoriels considérés en mathématiques sont des sous-espaces d'espaces fonctionnels. Donnons d'autres exemples.

Généralisation des espaces de suites à support fini

Soit $X$ un ensemble quelconque. Considérons l'espace vectoriel $F$ de toutes les applications de $X$ dans $\mathbb{K}$ qui s'annulent partout sauf en nombre fini de points de $X$ .

Alors $F$ est un sous-espace vectoriel de l'espace vectoriel de toutes les applications de $X$ vers $\mathbb{K}$ . Pour le voir, remarquez que la réunion de deux ensembles finis est finie et ainsi la somme de deux applications de $F$ s'annulera encore en un nombre fini de points.

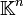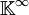Si $X$ est l'ensemble des entiers compris entre 1 et $n$ alors cet espace peut facilement être assimilé à l'espace des $n$ -uplets $\mathbb{K}^n$ . De façon similaire, si $X$ est l'ensemble des entiers naturels $\mathbb{N}$ , alors cet espace n'est autre que $\mathbb{K}^{\infty}$ .

Une base naturelle de $F$ est l'ensemble des fonctions $f x$ où $x$ appartient à $X$ , telles que

$f_x(y) = \begin{cases}1 \quad x = y \\ 0 \quad x \neq y\end{cases}$

La dimension de $F$ est ainsi égal au cardinal de $X$ . De cette façon, nous pouvons construire un espace vectoriel de n'importe quelle dimension sur n'importe quel corps. De plus tout espace vectoriel est isomorphe à un espace vectoriel de cette forme. Tout choix d'une base détermine un isomorphisme en envoyant cette base sur une base déterminée de $F$ .

Applications linéaires

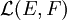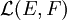Un exemple important issu de l'algèbre linéaire est l'espace vectoriel des applications linéaires. Soit $\mathcal{L}(E,F)$ l'ensemble des applications linéaires de $E$ dans $F$ ( $E$ et $F$ étant des espaces vectoriels sur le même corps commutatif $\mathbb{K}$ ). Alors $\mathcal{L}(E,F)$ est un sous-espace vectoriel de l'espace des applications de $E$ vers $F$ puisqu'il est stable pour l'addition et la multiplication par un scalaire.

Remarquons que 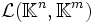$\mathcal{L}(\mathbb{K}^n, \mathbb{K}^m)$ peut être identifié à l'espace vectoriel des matrices 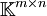$\mathbb{K}^{m\times n}$ de manière naturelle. En fait, en choisissant une base appropriée des espaces vectoriels de dimension finie $E$ et $F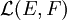$ , $\mathcal{L}(E,F)$ peut aussi être identifié à 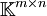$\mathbb{K}^{m\times n}$ . Cette identification dépend naturellement du choix des bases.

Applications continues

Si $X$ est un espace topologique, tel que l'intervalle unité $[0,1]$ , alors nous pouvons considérer l'espace vectoriel des applications continues de $X$ dans $\mathbb{R}$ . C'est un sous-espace vectoriel de toutes les fonctions réelles définies sur $X$ puisque la somme de deux applications continues quelconques est continue et la produit par un scalaire d'une application continue est continue.

Équations différentielles

Le sous-ensemble de l'espace vectoriel des applications de $\mathbb{R}$ dans $\mathbb{R}$ formé d'applications satisfaisant des équations différentielles linéaires est aussi un sous-espace vectoriel de ce dernier. Cela vient du fait que la dérivation est une application linéaire, c'est-à-dire $(a f + b g)' = a f' + b g'$ où $'$ désigne cette application linéaire (aussi appelée opérateur linéaire).

Extensions de corps

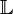Supposons que $\mathbb{K}$ soit un sous-corps de $\mathbb{L}$ (voir extension de corps). Alors 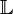$\mathbb{L}$ peut être vu comme un espace vectoriel sur $\mathbb{K}$ en restreignant la multiplication par un scalaire à l'ensemble $\mathbb{K}$ (l'addition vectorielle étant définie normalement). La dimension de cet espace vectoriel est appelée degré de l'extension. Par exemple l'ensemble des nombres complexes $\mathbb{C}$ forme un espace vectoriel de dimension deux sur le corps des réels $\mathbb{R}$ . Cependant, l'ensemble $\mathbb{R}$ des nombres réels forme un espace vectoriel (non dénombrable) de dimension infinie sur le corps des rationnels $\mathbb{Q}$ .

Si $E$ est un espace vectoriel sur 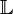$\mathbb{L}$ , alors $E$ peut être aussi vu comme un espace vectoriel sur $K$ . Les dimensions sont liées par la formule:

${\rm dim}_{\mathbb{K}} E=\left({\rm dim}_{\mathbb{L}}E\right)\left({\rm dim}_{\mathbb{K}} \mathbb{L}\right)$

Par exemple 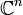$\mathbb{C}^n$ , peut être considéré comme un espace vectoriel sur le corps des réels, de dimension $2 n$ .

Espaces vectoriels finis

À part l'espace nul qui est de dimension zéro sur n'importe quel corps, un espace vectoriel sur un corps $\mathbb{K}$ a un nombre fini d'éléments si et seulement si $\mathbb{K}$ est un corps fini et l'espace vectoriel est de dimension finie.

Ainsi 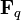$\mathbf{F}_q$ est l'unique corps fini de cardinal $q$ , où $q$ est un entier qui doit être une puissance d'un nombre premier ( $q = p m$ , $p$ étant premier). Alors tout espace vectoriel $E$ de dimension $n$ sur 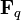$\mathbf{F}_q$ aura $q n$ éléments. Remarquez que le nombre d'éléments de $E$ est aussi une puissance d'un nombre premier. 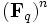Le premier exemple d'un tel espace, est celui des $n$ -uplets $\left(\mathbf{F}_q\right)^n$ .

Portail des mathématiques

Ce document provient de « Exemples d%27espaces vectoriels ».

Catégorie : Espace vectoriel

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Exemples D'espaces Vectoriels de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Exemples d'espaces vectoriels — Cette page présente une liste d exemples d espaces vectoriels. Vous pouvez consulter l article espace vectoriel pour y trouver les définitions des notions employées ci dessous. Voyez également les articles sur la dimension, les bases. Nous… … Wikipédia en Français
Espaces vectoriels — Espace vectoriel En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont… … Wikipédia en Français
TOPOLOGIQUES (ESPACES VECTORIELS) — La théorie des espaces normés, développée par S. Banach et ses élèves, s’est vite révélée insuffisante pour les besoins de l’analyse fonctionnelle où interviennent de nombreux espaces vectoriels munis d’une topologie qui n’est pas déduite d’une… … Encyclopédie Universelle
NORMÉS (ESPACES VECTORIELS) — L’analyse fonctionnelle linéaire, en tant que théorie générale, s’est créée au début du XXe siècle, autour des problèmes posés par les équations intégrales. Entre 1904 et 1906, D. Hilbert (1862 1943) est amené à étudier des développements en… … Encyclopédie Universelle
Espaces euclidiens — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique … Wikipédia en Français
MÉTRIQUES (ESPACES) — La notion d’espace métrique, introduite en 1906 par M. Fréchet et développée peu après par F. Hausdorff, est directement issue d’une analyse des principales propriétés de la distance usuelle. L’extension aux espaces métriques des propriétés de… … Encyclopédie Universelle
Espace vectoriel — En algèbre linéaire, un espace vectoriel est un ensemble muni d une structure permettant d effectuer des combinaisons linéaires. Étant donné un corps K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée +) muni d une… … Wikipédia en Français
Espace Vectoriel — En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée… … Wikipédia en Français
Espace vectoriel linéaire — Espace vectoriel En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont… … Wikipédia en Français
R² — Espace vectoriel En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Exemples D'espaces Vectoriels