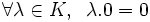Espace Nul
- Espace Nul
-
Espace nul
En algèbre linéaire, l'espace nul sur un corps K est l'unique K-espace vectoriel de dimension 0. Cet espace ne possède qu'un unique élément, noté 0. Les lois d'addition et de multiplication scalaire sont les suivantes :
- 0 + 0 = 0
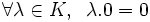
L'espace nul vérifie les propriétés remarquables suivantes :
- L'espace nul est l'unique structure d'espace vectoriel de cardinal 1. Si K est un corps infini, c'est l'unique espace vectoriel fini sur K.
- L'espace nul comporte une unique base, et cette base ne contient aucun vecteur (elle est indexée par l'ensemble vide).
- L'espace nul est à isomorphisme près le seul espace vectoriel à se plonger dans tous les K-espaces vectoriels. De plus le plongement de l'espace nul dans un K-espace vectoriel donné est unique, c'est l'application nulle.
- En d'autres termes, l'espace nul est l'objet initial de la catégorie des K-espaces vectoriels.
- L'espace nul est à isomorphisme près le seul espace vectoriel sur lequel se surjecte tout K-espace vectoriel. De plus, la surjection d'un K-espace vectoriel donné sur l'espace nul est unique, c'est l'application nulle.
- En d'autres termes, l'espace nul est l'objet final de la catégorie des K-espaces vectoriels.
- En topologie, pour K=R, l'espace nul est appelé le point. Il figure dans certaines séries d'espaces topologiques, dont la série des simplexes.
- Dans un espace vectoriel euclidien E, l'orthogonal de E est l'espace nul, et l'orthogonal de l'espace nul est E.
Structure additionnelle
Soit E = {0} l'espace nul. L'identité 0.0=0 définit une loi produit sur E. Pour autant, E n'est pas considéré comme un anneau. Il vérifie toutes les propriétés de compatibilité entre les structures additive et multiplicative. Cependant, pour éviter ce cas critique, on demande que l'élément 1 diffère de l'élément 0.
 Portail des mathématiques
Portail des mathématiques
Catégories : Espace vectoriel | Zéro
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Espace Nul de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace nul — En algèbre linéaire, l espace nul sur un corps commutatif K est le singleton {0}, muni de son unique structure de K espace vectoriel. Les lois d addition et de multiplication par un scalaire sont données comme suit : 0 + 0 = 0 ; . Son… … Wikipédia en Français
Espace Vectoriel — En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée… … Wikipédia en Français
Espace vectoriel linéaire — Espace vectoriel En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont… … Wikipédia en Français
Espace vectoriel — En algèbre linéaire, un espace vectoriel est un ensemble muni d une structure permettant d effectuer des combinaisons linéaires. Étant donné un corps K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée +) muni d une… … Wikipédia en Français
Espace vectoriel topologique — Les espaces vectoriels topologiques sont une des structures de base de l analyse fonctionnelle. Ce sont des espaces munis d une structure topologique associée à une structure d espace vectoriel, avec des relations de compatibilité entre les deux… … Wikipédia en Français
Espace vectoriel fini — Hormis l espace nul, les espaces vectoriels finis, c est à dire, de cardinal fini, sont exactement les espaces vectoriels de dimension finie sur les corps finis. Se posent des questions de combinatoire, comme le calcul du nombre de bases, ou du… … Wikipédia en Français
Espace Préhilbertien — En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la dimension finie. Le cas… … Wikipédia en Français
Espace prehilbertien — Espace préhilbertien En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d un produit scalaire. Cette notion généralise celles d espace euclidien ou hermitien, en omettant l hypothèse de la… … Wikipédia en Français
Espace Euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… … Wikipédia en Français
Espace euclidien (algèbre linéaire) — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique … Wikipédia en Français