- Espace symetrique
-
Espace symétrique
En mathématiques, et plus spécifiquement en géométrie différentielle, un espace symétrique est une variété riemannienne qui est un espace homogène et pour laquelle le tenseur de Riemann est covariantement constant.
Ces espaces ont été définis et classifiés pour la première fois par Élie Cartan. Ils constituent un cadre naturel pour généraliser l'analyse harmonique classique sur les sphères.
Sommaire
Définition géométrique des espaces symétriques
En géométrie riemannienne, un espace localement symétrique est une variété riemannienne (M,g) telle que, (localement) autour de chaque point x, il existe une symétrie σx qui inverse les géodésiques issues de x et qui est une isométrie (locale).
Un espace localement symétrique est dit symétrique si les symétries peuvent se prolonger à tout l'espace. De manière équivalente, une variété riemannienne (M,g) est dite symétrique lorsque, pour tout point x de M, il existe une isométrie σx:M
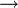M vérifiant :- σx(x) = x ;
- dσx(x) = − Id.
Cette isométrie σx est appelée l'involution en x.
Propriétés remarquables
- Tout espace symétrique est une variété riemannienne géodésiquement complète, donc complète en vertu du théorème de Hopf-Rinow.
- Il existe une et une unique involution en x.
- Le tenseur de courbure d'une variété riemannienne est parallèle.
Exemples d'espaces symétriques
- Les sphères, les espaces projectifs sont des espaces symétriques.
- les espaces de courbure sectionnelle constante sont des espaces localement symétriques.
- Les espaces hyperboliques sont des espaces symétriques de rang 1.
- Les espaces d'Heisenberg sont des espaces symétriques.
Classification des espaces symétriques
Classification
La classification des variétés symétriques est aujourd'hui connue :
- Les sphères euclidiennes,
- Les espaces hyperboliques,
- Les espaces projectifs,
- Sl(n,R)/SO(n,R),
- Sp(p+q)/Sp(p)xSp(q),
- ..
Espaces symétriques compacts
Espaces symétriques non-compacts
Analyse harmonique sur les espaces symétriques
Historique
La théorie et la classification des espaces symétriques sont l'œuvre de Elie Cartan.
Bibliographie
articles
- M. Berger : Sur les groupes d'holonomie des variétés riemanniennes non symétriques, 1953.
- M. Berger : Structure et classification des espaces homogènes symétriques à groupe d'isométrie semi-simple, M. Berger, 1955.
- M. Berger : Les espaces symétriques non compacts, 1957.
- M. Berger : Sur quelques variétés d'Einstein compactes, 1962.
livres
- (en) Besse, Einstein manifolds ISBN 0-387-15279-2.
- (en) S. Helgason, Differential geometry, Lie groups, and symmetric spaces, Academic Press, 1978. ISBN 0-8218-2848-7. La référence sur les espaces symétriques.
Voir aussi
Portail de la géométrie
Catégorie : Géométrie riemannienne
Wikimedia Foundation. 2010.
