Espace réciproque

En physique, on utilise souvent des espaces abstraits pour caractériser les phénomènes, ce sont des espaces des phases.

Dans le cas des ondes, l'espace des phases est l'espace des vecteurs d'onde. Une onde plane et monochromatique est entièrement caractérisée par son vecteur d'onde. Or, la diffusion Rayleigh transforme une onde plane monochromatique en une somme d'ondes planes monochromatiques ; l'amplitude diffusée selon un vecteur d'onde donné $\vec{K}$ est le produit de l'amplitude incidente $ψ 0$ par une fonction du vecteur d'onde $\vec{K}$ :

$\psi_{\vec{K}}=\psi_0 \cdot F(\vec{K})$

où $F$ correspond à la transformée de Fourier 3D de l'objet diffractant l'onde (voir théorie de la diffraction sur un cristal).

Du point de vue mathématique, les vecteurs d'ondes ont la spécificité d'être les vecteurs propres des transformations linéaires, homogènes et continues (pouvant se formuler à l'aide d'un produit de convolution). La solution de nombreux problèmes physiques peut donc s'écrire comme une somme d'ondes planes monochromatiques.

Si les opérations sur les vecteurs d'onde n'ont pas de traduction immédiate dans l'espace habituel (c'est une représentation dans l'espace des fréquences spatiales), son rôle en physique est essentiel. L'espace des phases a alors une correspondance avec l'espace direct, on parle d'espace réciproque.

De part les relations de Planck, l'espace des vecteurs d'ondes $\vec{K}$ est l'espace des vecteurs impulsion et la représentation dans l'espace $(E,\vec{K})$ et dual de $(E, x, y, z)$ . L'espace réciproque correspond à une représentation ondulatoire des objets (fréquentielle), duale de leur représentation corpusculaire (spatiale). Le célèbre principe d'incertitude de Heisenberg est l'expression physique du lien de dualité entre les deux représentations.

Un point remarquable est qu'un objet de type réseau cristallin est également un réseau du point de vue ondulatoire. On parle alors de réseau réciproque. L'espace réciproque est ainsi fréquemment utilisé en cristallographie et en physique du solide, ainsi qu'en diffraction dans le domaine optique.

Sommaire

1 Le vecteur d'onde
2 Diffusion Rayleigh et principe de Huygens d'une onde
3 Conventions de notation pour l'article
4 Exemples
5 Association de réseaux
6 Indexation du réseau réciproque et plans de l'espace réel
7 Utilisation en cristallographie
8 Notes
9 Voir aussi
- 9.1 Bibliographie
- 9.2 Articles connexes

Le vecteur d'onde

La phase d'une onde varie en fonction du temps et de l'endroit considéré.

$\psi(\vec{x},t) = \psi_0 \cdot \exp \left ( i \cdot \left (\omega \cdot t + \varphi(\vec{x}) + \varphi_0 \right ) \right )$

Pour simplifier, on prend φ₀ nul à l'origine O du repère. Le terme spatial s'exprime sous la forme d'un produit scalaire :

$\varphi(\vec{x}) = -\vec{k} \cdot \vec{x}$

où $\vec{x}$ est le vecteur reliant l'origine O (φ = 0) au point considéré. La norme de $\vec{k}$ est 2π/λ (en rad·m^-1), λ étant la longueur d'onde^[1].

La « raison d'exister » du vecteur d'onde est le produit scalaire. Si l'on note $f_{\vec{k}}$ la fonction :

$f_{\vec{k}}(\vec{x}) = \vec{k} \cdot \vec{x}$

on voit que cette fonction est une forme linéaire ; l'ensemble de ces formes linéaires est un espace vectoriel isomorphe à l'espace des phases. De fait, l'espace des phases est un espace dual.

Physiquement, le vecteur d'onde $\vec{k}$ correspond à une description ondulatoire d'un objet (onde plane monochromatique) alors que le vecteur position $\vec{x}$ correspond à une description corpusculaire. Selon le principe d'incertitude de Heisenberg, les deux descriptions sont intimement liées et un objet réel ne peux qu'être approximativement décrit par l'une ou l'autre puisqu'il n'est ni monochromatique ni parfaitement localisé. Seule la fonction d'onde décrit complètement l'objet, et ce, quelle que soit la base utilisée (fréquentielle ou spatiale).

Diffusion Rayleigh et principe de Huygens d'une onde

L'espace réciproque n'est utile que lorsque l'on considère une onde monochromatique. Cette onde est représentée par un vecteur $\vec{k}$ unique.

Lorsque cette onde interagit avec une particule, elle peut être diffusée de manière élastique, par diffusion Rayleigh. De manière générale, pour une onde plane, on peut considérer en tout point une diffusion isotrope selon le principe de Huygens.

Les vecteurs diffusés $\vec{k'}$ ont la même norme que $\vec{k}$ mais une direction différente ; dans l'espace réciproque, leur extrémité forme une sphère de rayon $k = ||\vec{k}||$ . On ne s'intéresse qu'à une direction de diffusion à la fois, donc à un seul vecteur $\vec{k'}$ .

Considérons un centre de diffusion situé en $\vec{r}$ . Le déphasage spatial par rapport à l'origine est

$\varphi_1 (\vec{r}) = -\vec{k} \cdot \vec{r}$ .

Si l'on s'intéresse au déphasage de l'onde diffusée en un point $\vec{x}$ , le déphasage spatial entre la source $\vec{r}$ et le point $\vec{x}$ vaut

$\varphi_2 (\vec{x}) = -\vec{k'} \cdot (\vec{x} - \vec{r})$

puisque l'onde a parcouru un chemin $\vec{x} - \vec{r}$ . Le déphasage total en $\vec{x}$ vaut donc

$\varphi_1 (\vec{r}) + \varphi_2 (\vec{x}) = -\vec{k} \cdot \vec{r} - \vec{k'} \cdot (\vec{x} - \vec{r})$

si l'on pose

$\vec{K} = \vec{k'} - \vec{k}$

on obtient

$\varphi_1 (\vec{r}) + \varphi_2 (\vec{x}) = \vec{K} \cdot \vec{r} - \vec{k'} \cdot \vec{x}$

on a donc un terme qui ne dépend que de la position du centre de diffusion, et un autre terme qui ne dépend que du point final considéré, ce qui simplifie les calculs.

Le vecteur $\vec{K}$ est appelé vecteur de diffraction.

Comme l'extrémité des vecteurs $\vec{k'}$ est sur la sphère de centre O et de rayon k, l'extrémité des vecteurs $\vec{K} = \vec{k'} - \vec{k}$ est sur la sphère dont le centre est la translation de l'origine par $- \vec{k}$ , et de rayon k.

Conventions de notation pour l'article

Dans les exemples suivants, nous considérons que l'espace est muni d'une base orthonormée directe $(\vec{e_1},\vec{e_2},\vec{e_3})$ , ces vecteurs définissant respectivement les axes x, y et z.

Le plan contenant les fentes d'Young, le réseau ou les lames de verre est le plan (y,z) ; l'axe des x est normal à ce plan.

Les composantes du vecteur $\vec{K}$ sont notées K_x, K_y et K_z.

Exemples

Exemple des fentes de Young

Le problème des fentes de Young peut se traiter avec ce formalisme si l'on considère que l'onde incidente est plane et que l'écran est à l'infini.

L'onde incidente a pour équation :

$\psi(\vec{x},t) = \psi_0 \cdot e^{i\cdot \omega \cdot t - i \cdot \vec{k} \cdot \vec{x}}$

les fentes ont pour coordonnées S₁(0,d) et S₂(0,0) (on place l'origine à la fente du bas),
le vecteur d'onde incident a pour composantes $\vec{k}\,(k\,,0)$

alors en $\vec{x}$ , l'onde diffusée par la fente S₂ vaut

$\psi_2 (\vec{x},t) = \psi_0 \cdot e^{i\cdot \omega \cdot t - i\cdot \vec{k'} \cdot \vec{x}}$

et celle diffusée par S₁ vaut

$\psi_1 (\vec{x},t) = \psi_0 \cdot e^{i\cdot \omega \cdot t - i\cdot (\vec{k'}\cdot \vec{x}- \vec{k'} \cdot \overrightarrow{S_2 S_1} + \vec{k} \cdot \overrightarrow{S_2 S_1} )} = \psi_0 \cdot e^{i\cdot \omega \cdot t + i\cdot \vec{K} \cdot \overrightarrow{S_2 S_1} - i\cdot \vec{k'} \cdot \vec{x}} = \psi_2 (\vec{x},t) \cdot e^{\vec{K} \cdot \overrightarrow{S_2 S_1}}$

où $\overrightarrow{S_2 S_1}$ est le vecteur (0,d). L'interférence des deux ondes diffusées donne :

$\psi_1 (\vec{x},t) + \psi_2 (\vec{x},t) = \psi_2 (\vec{x},t) \cdot \left (1+ e^{i\cdot \vec{K} \cdot \overrightarrow{S_2 S_1}} \right )$

L'amplitude de l'onde dépend du facteur de droite, donc du produit scalaire $\vec{K} \cdot \overrightarrow{S_2 S_1}$ . Si on considère une diffusion d'un angle $\alpha \in\,]-\,\pi/2\,, \pi/2[$ par rapport à l'incidence, on a :

$\vec{k} = k \cdot (1\,,0)$

$\vec{k'} = k \cdot (\cos \alpha\,, \sin \alpha)$

donc

$\vec{K} = \vec{k'} - \vec{k} = k \cdot (\cos \alpha-1\,, \sin \alpha) = k \cdot (\vec{e_1} \cos \alpha + \vec{e_2} \sin \alpha) - k \cdot \vec{e_1}$

on remarque ici que la pointe du vecteur $\vec{K}$ décrit un demi-cercle centré en (-k, 0) et de rayon k (demi-cercle car $\alpha \in\,]\,\pi/2\,, \pi/2[$ ).

Transposition dans l'espace réciproque du problème des fentes de Young pour λ/d = 0,2 ; les points représentent les conditions de diffraction

Réseau réciproque des fentes de Young

D'après l'équation qui précède, on a :

$\vec{K} \cdot \overrightarrow{S_2 S_1} = k \cdot d \cdot \sin \alpha$

L'amplitude de l'onde est maximale lorsque le produit scalaire est un multiple de 2π. Comme k = 2π/λ, on retrouve bien que

$d \cdot \sin \alpha = n \cdot \lambda \qquad \mbox{avec}\ n \in \mathbb{Z}$

Par ailleurs, on a :

$\overrightarrow{S_2S_1} = d \cdot \vec{e_2}$

et donc

$\vec{K} \cdot \overrightarrow{S_2 S_1} = K_y \cdot d$

La condition de diffraction devient alors

$K_y = \frac{2 \pi n}{d}$

donc pour les conditions d'intensité maximale, K_y ne dépend que de n et pas de λ.

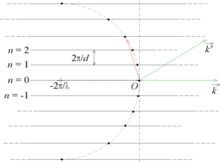
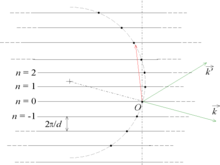
Les conditions sur $\vec{K}$ peuvent donc se représenter de manière graphique dans l'espace des phases : l'extrémité du vecteur de diffraction se situe aux points d'intersection du demi-cercle de centre

(-k = -2π/λ , 0) et de rayon k = 2π/λ avec les droites horizontales d'équation K_y = 2πn/d.

On voit donc que le système des fentes de Young d'écartement d, éclairées par onde incidente de longueur d'onde λ, peut se représenter par un ensemble de points (K₁, K₂..., K_n), définissant l'extrémité des vecteurs $\vec{K}$ pour lesquels l'intensité est maximale.

Utilisation du réseau réciproque pour une incidence oblique

La construction du réseau réciproque prend en compte uniquement le vecteur de diffraction $\vec{K}$ , mais pas le vecteur d'onde incident $\vec{k}$ ; ainsi, si l'onde incidente était oblique, il suffirait de faire changer le centre du demi-cercle (qui se trouve toujours à la position $-\,\vec{k}$ par rapport à l'origine) ; l'intersection de ce demi-cercle avec le réseau réciproque donnerait toujours les conditions de diffraction, c'est-à-dire permettrait de déduire les vecteurs $\vec{k'}$ pour lesquels on a un maximum d'intensité.

On peut même s'afranchir de l'invariance par translation et travailler en trois dimensions, en considérant des rayons (incidents ou diffractés) hors du plan $(\vec{e_1},\vec{e_2})$ . Le vecteur $\vec{k'}$ pouvant prendre toutes les orientations, il décrit une demi-sphère, il en est de même pour le vecteur $\vec{K}$ . L'équation K_y = 2πn/d est alors l'équation d'un plan ; les conditions de diffraction sont donc l'intersection de la demi-sphère correspondant au vecteur d'onde incident avec ces plans de l'espace réciproque. Ce sont donc des demi-cercles.

Ce réseau de plans horizontaux est le réseau réciproque des fentes de Young. On remarque que :

les plans du réseau réciproque sont perpendiculaires au vecteur de translation $\overrightarrow{S_2 S_1}$ entre les fentes ;
l'espacement des droites est inversement proportionnel à l'espacement des fentes.

Exemple du réseau de diffraction

Réseau en réflexion

Considérons un réseau de diffraction optique de pas p.

Pour le calcul, on définit la fonction de l'onde diffractée par le j ^e trait par

$\psi_j (\vec{x},t) = \psi_0 \cdot e^{i\cdot \omega \cdot t + i\cdot j\cdot p \cdot \vec{K} \cdot \vec{e_1} - i\cdot \vec{k'}\cdot \vec{j}}$

si p est le pas du réseau et $\vec{e_1}$ l'axe des x. La fonction d'onde totale est donc

$\psi (\vec{x},t) = \sum_j \psi_j (\vec{x},t)$

soit

$\psi (\vec{x},t) = \psi_0 \cdot e^{i\cdot \omega \cdot t - i\cdot \vec{k'}\cdot \vec{j}} \cdot \sum_j e^{i\cdot j\cdot p \cdot \vec{K} \cdot \vec{e_1} }$

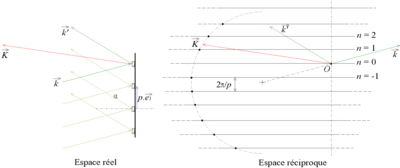
Les conditions de diffraction sont similaires à celles des fentes de Young, seule change la largeur des raies. Le réseau réciproque est donc le même. Toutefois, on travaille fréquemment en réflexion. Dans ce cas-là, c'est le demi-cercle complémentaire qu'il faut envisager.

Exemple des interférences par une lame d'air

Interférence par une lame d'air : perspective cavalière dans l'espace réel, vue de profil dans l'espace réciproque

Les interférences par une lame d'air sont créées par la réflexion selon deux plans parallèles séparées d'une distance d. On regarde les interférences « à l'infini ».

Soit $\vec{x}$ le vecteur normal aux plans et de longueur d. Considérons, pour simplifier, que les deux plans sont parallèles au plan (y,z), et prenons deux rayons parallèles incidents de vecteur d'onde $\vec{k}$ frappant les plans à des points situés sur le même axe $\vec{x}$ (le déphasage est indépendant de la position sur le plan mais ne dépend que de la direction de diffusion). Si $\vec{e_1}$ est l'axe des x, on a $\vec{x} = d \cdot \vec{e_1}$ .

Le rayon frappant le plan superficiel est directement diffusé. Le rayon frappant le plan profond est diffusé après avoir subi un déphasage Δφ₁

$\Delta \varphi_1 = -\vec{k} \cdot \vec{x}$

Considérons un vecteur d'onde diffusé $\vec{k'}$ . Sur un front d'onde donné (plan perpendiculaire aux vecteurs d'onde), le rayon diffusé par le plan profond subit encore un déphasage Δφ₂

$\Delta \varphi_2 = -\vec{k'} \cdot (-\vec{x})$

Le déphasage total est donc

$\Delta \varphi = \Delta \varphi_1 + \Delta \varphi_2 = \vec{K} \cdot \vec{x}$

L'interférence est constructrice si

Δφ = 2 n π

c'est-à-dire si

$\vec{K} \cdot \vec{x} = 2n \pi$

donc

$K_x = \frac{2n \pi}{d}$

si K_x est la composante de $\vec{K}$ selon l'axe des x. On voit donc que les conditions d'interférences constructrices sont représentées, dans l'espace des phases, par des plans parallèles à (y,z) et espacés de 2π/d.

Comme précédemment, pour un vecteur incident $\vec{k}$ donné, les conditions de diffraction sont données par l'intersection entre ces plans de l'espace réciproque et la sphère décrite par l'extrémité de $\vec{K}$ . Ces intersections sont des cercles ; si l'extrémité de $\vec{K}$ décrit un cercle, celle de $\vec{k'}$ également, donc les rayons diffusés en conditions d'interférences constructrices donnent des cônes d'axe normal aux plans.

Note: Contrairement aux cas précédents, il n'y a plus ici d'invariance par translation selon l'axe des z, il faut donc se placer en trois dimensions.

On peut considérer un nombre « infini » de plan parallèles, et donc une sorte de réseau de plans. La différence serait alors la même qu'entre les fentes de Young et le réseau plan : les positions de diffraction sont les mêmes, seule change la largeur des raies.

Dans le cas où l'on considère une direction de diffusion symétrique à la direction d'incidence, et si l'on note θ l'angle entre le rayon incident et le plan, on a

$K_x = \frac{2 \pi \sin \theta}{\lambda}$

( $\vec{K}$ est normal aux plans) et l'on retrouve la loi habituelle $2 d sin θ = n λ$ .

Association de réseaux

Association de deux réseaux sur un même plan

Il est possible d'associer les réseaux deux par deux ; les rayons doivent alors vérifier les deux conditions de diffraction, ce qui revient à prendre l'intersection des réseaux réciproques.

Diffraction par deux réseaux croisés : le réseau réciproque est une forêt de droites (en rouge)

Prenons par exemple deux réseaux plans d'orientation différente, c'est-à-dire un quadrillage du plan $(\vec{e_2},\vec{e_3})$ . Les réseaux réciproques sont des plans perpendiculaires aux vecteurs de translation des réseaux. L'intersection entre deux plans non parallèles est une droite ; le réseau réciproque de ce quadrillage est donc une « forêt » de droites parallèles à $\vec{e_1}$ .

Pour un vecteur $\vec{k}$ donné, les directions dans lesquelles se trouvent taches de diffraction sont déterminées par l'intersection entre la demi-sphère des $\vec{K}$ et cette forêt de droites.

Appelons R₁ le premier réseau ; le vecteur de translation entre deux traits, normal aux traits, est noté $\vec{x_1}$ , le vecteur directeur unitaire des traits est noté $\vec{u_1}$ et le réseau réciproque de plans est noté R^*₁. Le second réseau est noté R₂, son vecteur de translation est $\vec{x_2}$ , son vecteur directeur unitaire est $\vec{u_2}$ et le réseau réciproque est R^*₂. On note $\vec{u_3} = \pm \vec{e_1}$ ; le signe est choisi en fonction de l'orientation de $\vec{u_1}$ et de $\vec{u_2}$ afin que le trièdre $(\vec{u_1},\vec{u_2},\vec{u_3})$ soit direct ; on note que cette famille forme une base.

Les plans de R^*₁ sont perpendiculaires à $\vec{x_1}$ et sont espacés de 2π/||x'₁||, ceux de R^*₂ sont perpendiculaires à $\vec{x_2}$ et sont espacés de 2π/||x'₁||. Si l'on définit une nouvelle base $(\vec{e_1^*},\vec{e_2^*},\vec{e_1})$

$\vec{e_2^*} = \frac{2 \pi}{||\vec{x_1}||^2} \cdot \vec{x_1}$

$\vec{e_1^*} = \frac{2 \pi}{||\vec{x_2}||^2} \cdot \vec{x_2}$

(l'inversion des indices est purement conventionnelle et est expliquée ci-après), alors dans cette base, les plans de R^*₂ ont pour équation

K_x = a, a étant un nombre entier

les plans de R^*₁ ont pour équation

K_y = b, b étant un nombre entier

et donc les droites représentant les conditions de diffraction ont pour équation

$\left\{\begin{matrix} K_x = a \\ K_y = b \end{matrix}\right.$

Dans la pratique, on se réfère plutôt aux vecteurs directeurs des traits des réseaux, et on définit

$\vec{e_1^*} = \frac{2 \pi}{||\vec{x_1}||} \cdot \frac{1}{||\vec{u_2} \wedge \vec{u_3}||} \cdot \vec{u_2} \wedge \vec{u_3}$

$\vec{e_2^*} = \frac{2 \pi}{||\vec{x_2}||} \cdot \frac{1}{||\vec{u_3} \wedge \vec{u_1}||} \cdot \vec{u_3} \wedge \vec{u_1}$

$\vec{e_3^*} = \frac{1}{||\vec{u_1} \wedge \vec{u_2}||} \cdot \vec{u_1} \wedge \vec{u_2}$

le vecteur $\vec{e_3^*}$ n'a pas d'utilité pratique ici mais permet de définir de manière systématique une nouvelle base. L'inversion des indices est justifiée ici par une construction systématique de vecteurs de la base (permutation circulaire des indices).

Maintenant, considérons que $\vec{u_1}$ joint deux intersections de R₁ et de R₂, idem pour $\vec{u_2}$ . Soit V le volume du parallélépipède formé par $\vec{u_1}$ , $\vec{u_2}$ et $\vec{u_3}$ . On a :

$V = (\vec{u_1} \wedge \vec{u_2}) \cdot \vec{u_3} = (\vec{u_3} \wedge \vec{u_1}) \cdot \vec{u_2} = (\vec{u_2} \wedge \vec{u_3}) \cdot \vec{u_1}$

on a alors

$\vec{e_1^*} = \frac{2 \pi}{V} \cdot \vec{u_2} \wedge \vec{u_3}$

$\vec{e_2^*} = \frac{2 \pi}{V} \cdot \vec{u_3} \wedge \vec{u_1}$

$\vec{e_3^*} = \frac{2 \pi}{V} \cdot \vec{u_1} \wedge \vec{u_2}$

Cette base $(\vec{e_1^*},\vec{e_2^*},\vec{e_3^*})$ est appelée base réciproque. Elle est caractéristique des réseaux.

Réseaux sur des plans parallèles

La superposition de réseaux plans est équivalente à un réseau de fils à trois dimensions, ou encore à un réseau de points.

On peut aussi prendre des plans parallèles pourtant toutes un réseau identique, par exemple des plaques transparentes avec un réseau de traits réfléchissants (argenté). On choisit de prendre les plans parallèles à $\vec{e_1}$ , et les traites du réseau perpendiculaires à $\vec{e_2}$ .

Le réseau réciproque de ce montage est alors l'intersection entre les plans de l'espace réciproque, perpendiculaires à $\vec{e_1}$ , générés par la succession de plans réfléchissants, et les plans réciproques du réseau plan, perpendiculaires à $\vec{e_2}$ . Le réseau réciproque de ce montage est donc une série de droites parallèles à $\vec{e_3}$ .

On peut enfin envisager une succession de plans parallèles portant tous un quadrillage identique. Le réseau réciproque est l'intersection de trois réseaux de plans ; c'est donc un réseau de points. On voit que l'on obtient le même réseau de points dans l'espace réciproque pour plusieurs configurations dans l'espace réel, à partir du moment où les intersections des traits se trouvent au même endroit. Ce qui définit les directions dans lesquelles l'intensité est non nulle, ce sont les vecteurs $\vec{e_1}$ , $\vec{e_2}$ et $\vec{e_3}$ définissant la maille élémentaire.

On peut définir comme précédemment les vecteurs $\vec{e^*_1}$ , $\vec{e^*_2}$ et $\vec{e^*_3}$ de l'espace réciproque

$\vec{e_i^*} = \frac{2 \pi}{V} \cdot \vec{e_j} \wedge \vec{e_k}$

où (i, j, k) est une permutation circulaire de (1, 2, 3). Les vecteurs de diffraction $\vec{K}$ pour lesquels il y a diffraction vérifient

$\vec{K} = a \cdot \vec{e_1^*} + b \cdot \vec{e_2^*} + c \cdot \vec{e_3^*}$

où a, b et c sont des entiers. Le réseau réciproque est donc un réseau de points, les vecteurs $\vec{e^*_1}$ , $\vec{e^*_2}$ et $\vec{e^*_3}$ définissant une maille élémentaire de ce réseau réciproque.

Base réelle et base réciproque

D'après les propriétés du produit vectoriel, on a :

$\vec{e_1^*} \cdot \vec{e_2} = \vec{e_1^*} \cdot \vec{e_3} = 0$ , soit $\vec{e_1^*} \bot \vec{e_2}$ et $\vec{e_1^*} \bot \vec{e_3}$

$\vec{e_2^*} \cdot \vec{e_3} = \vec{e_2^*} \cdot \vec{e_1} = 0$ , soit $\vec{e_2^*} \bot \vec{e_3}$ et $\vec{e_2^*} \bot \vec{e_1}$

$\vec{e_3^*} \cdot \vec{e_1} = \vec{e_3^*} \cdot \vec{e_2} = 0$ , soit $\vec{e_3^*} \bot \vec{e_1}$ et $\vec{e_3^*} \bot \vec{e_2}$

Par ailleurs, si (i, j, k) est une permutation circulaire de (1, 2, 3), on a :

$\vec{e_i} \cdot \vec{e_i^*} = \frac{2\pi}{V} \cdot (\vec{e_i}\cdot \vec{e_j} \wedge \vec{e_k}) = 2\pi$ ^[2]

Indexation du réseau réciproque et plans de l'espace réel

Dans le cas d'un réseau de diffraction 3D (réseau de points dans l'espace), le réseau réciproque est également un réseau 3D. Chaque point du réseau réciproque ayant des coordonnées entières dans la base $(\vec{e_1^*},\vec{e_2^*},\vec{e_3^*})$ , on peut indexer chaque point par ses coordonnées.

À chaque point du réseau réciproque sont donc associés trois indices, notés habituellement (h, k, l), qui sont ses coordonnées.

Note: Jusqu'ici, les coordonnées entières étaient notées (a, b, c) afin d'éviter la confusion entre le vecteur d'onde $\vec{k}$ et l'indice réel k.

Nous avons vu que dans l'espace réel, ce qui importait, c'était le réseau de points, et que ces points pouvaient être les nœuds de quadrillages parallèles entre eux.

Prenons un point A(h, k, l) de l'espace des phases. La droite (O,A), passant par l'origine et par A, peut être vue comme l'image d'un réseau plan (cf. section Association de deux réseaux sur un même plan) ; ce réseau plan est porté par une famille P de plans parallèles.

Cette famille de plans de l'espace réel a pour image une famille de plans de l'espace réciproque (cf. section Exemple des interférences par une lame d'air). On peut donc dire que A représente une famille de plans parallèles équidistants ; plus A est éloigné de l'origine, plus les plans sont rapprochés.

Il est ainsi possible d'indexer les plan imaginaires contenant des nœuds du réseau réel : les plans associés à A portent les indices (h, k, l).

On peut montrer que ces indices sont les Indices de Miller (voir cet article pour la démonstration).

Utilisation en cristallographie

Article détaillé : Théorie de la diffraction sur un cristal.

Article détaillé : Réseau réciproque.

Un cristal est un réseau tridimensionnel d'atomes, d'ions ou de molécules. Chaque nuage électronique va provoquer de la diffusion Rayleigh, qui va être équivalent à la réflexion et à la transmisison des réseaux de trait. Le cristal est donc en quelques sortes un réseau qui fonctionne en réflexion et en transmission.

Le lieu des extrémités des vecteurs de diffraction $\vec{K}$ est donc une sphère complète, et non une demie sphère.

Notes

↑ Dans certains cas, la phase, en radians, est écrite $\varphi(\vec{x}) = 2\pi \cdot\vec{k} \cdot \vec{x}$ , la norme du vecteur d'onde est alors 1/λ, c'est le nombre d'onde ; le coefficient 2π ne change strictement rien au fond.
↑ Si le coefficient 2π ne fait pas partie de la définition du vecteur d'onde, on a alors $\vec{e_i} \cdot \vec{e_i^*} = 1$ .

Voir aussi

Bibliographie

J.-P. Eberhart, Méthodes physiques d'étude des minéraux et des matériaux solides, éd. Doin Éditeurs (Paris), 1976, pp 27, 52–58, 184–186, 477–479
B. D. Cullity, Elements of X-Ray Diffraction, éd. Addison-Wesley Publishing Co, 1956, pp 490–505
R. Jenkins, R. L. Snyder, X-Ray Powder Diffractometry, éd. Wiley -Interscience, 1996, pp 49–54

Regardez d'autres dictionnaires:

Espace Réciproque — En physique, on utilise souvent des espaces abstraits pour caractériser les phénomènes, ce sont des espaces des phases. Dans le cas des ondes, l espace des phases est l espace des vecteurs d onde. Une onde plane et monochromatique est entièrement … Wikipédia en Français
Espace reciproque — Espace réciproque En physique, on utilise souvent des espaces abstraits pour caractériser les phénomènes, ce sont des espaces des phases. Dans le cas des ondes, l espace des phases est l espace des vecteurs d onde. Une onde plane et… … Wikipédia en Français
espace réciproque — atvirkštinė erdvė statusas T sritis fizika atitikmenys: angl. reciprocal space vok. dualer Raum, m; reziproker Raum, m rus. обратное пространство, n pranc. espace réciproque, m … Fizikos terminų žodynas
Espace Des Phases — Courbes intégrales pour l équation du pendule simple dans l espace des phases (y,y ) En physique, l espace des phases est un espace abstrait dont les coordonnées sont les variables dynamiques du système étudié. Sommaire … Wikipédia en Français
Espace des phases — Courbes intégrales pour l équation du pendule simple dans l espace des phases , où est en abscisse et en ordonnée … Wikipédia en Français
Espace Topologique — La topologie générale est une branche des mathématiques qui fournit un vocabulaire et un contexte général pour traiter des notions de limite, de continuité, dans le cadre d un continuum ou d un espace discret, voire fini. Dans ce contexte, les… … Wikipédia en Français
Espace Vectoriel Topologique — Les espaces vectoriels topologiques sont une des structures de base de l analyse fonctionnelle. Ce sont des espaces munis d une structure topologique associée à une structure d espace vectoriel. Des exemples connus d espaces vectoriels… … Wikipédia en Français
Espace Localement Compact — En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les espaces… … Wikipédia en Français
ESPACE-TEMPS — La mécanique classique, sous la forme mathématique rigoureuse que lui a donnée Newton, repose sur les deux concepts fondamentaux d’espace et de temps absolus: un événement ponctuel est parfaitement déterminé lorsqu’on connaît sa position dans… … Encyclopédie Universelle
ESPACE (esthétique) — Le problème de l’espace n’aura été longtemps pour l’Occident que celui de la représentation de l’espace. Et la confusion perdure chez plus d’un théoricien. Or, des civilisations qui parfois même ne disposent d’aucun mot pour désigner le milieu à… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Espace réciproque

Sommaire

Le vecteur d'onde

Diffusion Rayleigh et principe de Huygens d'une onde

Conventions de notation pour l'article

Exemples

Exemple des fentes de Young

Exemple du réseau de diffraction

Exemple des interférences par une lame d'air

Association de réseaux

Association de deux réseaux sur un même plan

Réseaux sur des plans parallèles

Base réelle et base réciproque

Indexation du réseau réciproque et plans de l'espace réel

Utilisation en cristallographie

Notes

Voir aussi

Bibliographie

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Espace réciproque

Sommaire

Le vecteur d'onde

Diffusion Rayleigh et principe de Huygens d'une onde

Conventions de notation pour l'article

Exemples

Exemple des fentes de Young

Exemple du réseau de diffraction

Exemple des interférences par une lame d'air

Association de réseaux

Association de deux réseaux sur un même plan

Réseaux sur des plans parallèles

Base réelle et base réciproque

Indexation du réseau réciproque et plans de l'espace réel

Utilisation en cristallographie

Notes

Voir aussi

Bibliographie

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link