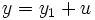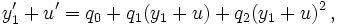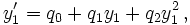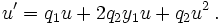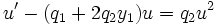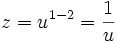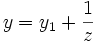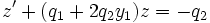- Equation de Riccati
-
Équation de Riccati
En mathématiques, une équation de Riccati est une équation différentielle ordinaire de la forme
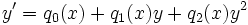 .
.
Où
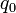 ,
, 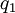 et
et 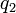 sont trois fonctions, souvent choisies continues à valeurs réelles sur un intervalle commun mais on les rencontre parfois à valeurs complexes.
sont trois fonctions, souvent choisies continues à valeurs réelles sur un intervalle commun mais on les rencontre parfois à valeurs complexes.Elle porte ce nom en l'honneur de Jacopo Francesco Riccati (1676-1754) et de son fils Vincenzo Riccati (1707-1775).
Il n'existe pas, en général, de résolution par quadrature à une telle équation mais, il existe une méthode de résolution dès que l'on en connaît une solution particulière.
Sommaire
Aspect historique
En 1720, Francesco Riccati présente à son ami, Giovanni Rizzetti, deux équations différentielles qu'il cherche à résoudre
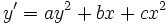 où a, b et c sont des constantes réelles (1)
où a, b et c sont des constantes réelles (1)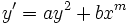 où a, b et m sont des constantes réelles (2)
où a, b et m sont des constantes réelles (2)
La première équation est issue de l'étude d'un mouvement plan vérifiant l'équation différentielle linéaire suivante
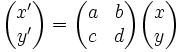 où x et y sont les coordonnées d'un point M en mouvement.
où x et y sont les coordonnées d'un point M en mouvement.
En s'intéressant à la pente z de la droite (OM), il prouve que z doit vérifier une équation du type (1), d'où son désir d'en étudier les solutions générales.
La seconde équation, ne fut résolue que partiellement par son auteur et par les Bernoulli (Nicolas 1er et Daniel tout particulièrement). Son fils, Vicenzo Riccati, en developpa une méthode de résolution par tractoire. Goldbach s'y attela aussi et plus récemment Liouville qui prouva (1841) qu'en dehors du cas
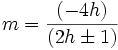 où h est un entier naturel,
où h est un entier naturel,
l'équation n'est pas résoluble par quadratures.
Les équations de Riccati se généralisent ensuite à toute équation de la forme
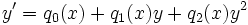 .
.
Pour certaines conditions sur
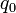 ,
, 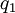 ,
, 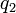 , l'équation est résoluble par quadrature. Grâce au théorème de Cauchy-Lipschitz, on prouve que, si
, l'équation est résoluble par quadrature. Grâce au théorème de Cauchy-Lipschitz, on prouve que, si 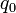 ,
, 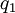 ,
, 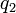 sont des fonctions continues, alors il existe des solutions à l'équation de Riccati. Enfin on démontre que, si l'on en connaît une solution particulière, une équation de Riccati se ramène par changement de variable, à une équation de Bernoulli.
sont des fonctions continues, alors il existe des solutions à l'équation de Riccati. Enfin on démontre que, si l'on en connaît une solution particulière, une équation de Riccati se ramène par changement de variable, à une équation de Bernoulli.Résolution connaissant une solution particulière
S'il est possible de trouver une solution y1, alors la solution générale est de la forme
En remplaçant
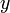 par
par 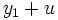
dans l'équation de Riccati, on obtient :
et comme
on a :
Or
qui est une équation de Bernoulli . La substitution nécessaire à la résolution de cette équation de Bernoulli est alors :
Substituer
directement dans l'équation de Riccati donne l'équation linéaire :
La solution générale de l'équation de Riccati est alors donnée par :
où z est la solution générale de l'équation linéaire citée ci-dessus.
Champs d'utilisation
On rencontre des équations de Riccati en physique quantique dans des problèmes portant sur l'équation de Schrödinger, dans l'équation des ondes, en commande optimale linéaire quadratique, en Commande LQG, ou bien encore dans l'équation de la propagation de la chaleur en régime sinusoïdal. Dans ces cas-là, la fonction q1 est une fonction à valeurs complexes.
On les rencontre également en mathématiques financières dans les problèmes portant sur la modélisation des taux d'intérêt. Plus particulièrement dans l'étude du modèle Cox-Ingersoll-Ross.
Références
- équation de Riccati sur le site de Serge Mehl : [ http://serge.mehl.free.fr/chrono/Riccati.html Chronomath].
- histoire des équations de Riccati
- équation de riccati résolution par quadrature par rené Lagrange
- Résolution par des tractoires
- Gallica, supplément de l'encyclopédie de Diderot (p 648 pour l'équation de Riccati)
Dans la célèbre Encyclopédie, Dictionnaire raisonné des Sciences, des Arts et des Métiers publiée sous la direction de Diderot, d'Alembert écrit :
- RICCATI (équation de) Algèbre. Calcul intégral. On appelle ainsi une équation différentielle du premier ordre à deux variables que le comte Ricati proposa aux géomètres vers 1720, & dont personne n'a encore donné de solution générale. Peut-être n'est-elle pas susceptible d'en avoir une en termes finis.
- Cette équation est de la forme dy + y2dx + axmdx = 0...
Catégorie : Équation différentielle
Wikimedia Foundation. 2010.