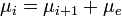- Equation de Saha
-
Équation de Saha
L'équation d'ionisation de Saha a été développée par l'astrophysicien indien Meghnad Saha en 1920. Une des applications importantes de l'équation était d'expliquer la classification spectrale. L'équation est le résultat de la combinaison des idées de mécanique quantique et de mécanique statistique.
Pour un gaz à assez haute température, les collisions thermiques des atomes ioniseront certains atomes. Un ou plusieurs des électrons qui sont normalement liés à l'atome dans les orbites, autour du noyau atomique, sera éjecté de l'atome et formera un gaz d'électrons co-existant avec le gaz des ions atomiques et des atomes neutres. Cet état de choses s'appelle un plasma. L'équation de Saha décrit le degré d'ionisation de ce plasma en fonction de la température, de la densité, et des énergies d'ionisation des atomes. L'équation de Saha se tient seulement pour les plasmas faiblement ionisés pour lesquels la longueur de Debye est grande. Ceci signifie que le « criblage » de la charge de Coulomb des ions et des électrons par d'autres ions et des électrons est négligeable. L'abaissement suivant des potentiels d'ionisation et de la « coupure » de la fonction de cloison est donc également négligeable.
Pour un gaz composé d'espèces atomiques simples, l'équation de Saha est la suivante :
Où:
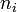est la densité des atomes dans leur i-ème état d'ionisation, c'est-à-dire avec i électrons arrachés.
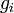est le niveau de dégradation énergétique des états pour les ions i-ème.
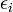est l'énergie requise pour supprimer i electrons d'un atome neutre, créant un i-niveau ionique.
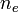est la densité d'électrons.
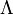est la longueur d'onde thermique de de Broglie d'un électron.
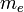est la masse d'un électron.
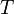est la température du gaz.
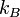est la constante de Boltzmann.
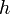est la constante de Planck.
Dans le cas où seulement un niveau d'ionisation est important, nous avons n tel que n = n0 + n1, l'équation de Saha simplifie à:
où ε est l'énergie d'ionisation.
L'équation de Saha est utile pour déterminer le rapport des densités de particules pour deux niveaux différents d'ionisation. La forme la plus utile de l'équation de Saha à cette fin est
,
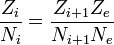là où Z provient de la fonction de partition en physique statistique. L'équation de Saha peut être vue comme un ajustement de l'état d'équilibre pour un potentiel chimique:
Cette équation déclare simplement que le potentiel pour un atome de l'état i d'ionisation de s'ioniser est identique que le potentiel pour un électron et un atome de l'état i+1 d'ionisation ; les potentiels sont égaux, donc le système est dans l'équilibre et aucun changement net d'ionisation ne se produira.
Liens externes
Catégorie : Thermodynamique
![\frac{n_{i+1}n_e}{n_i} = \frac{2}{\Lambda^3}\frac{g_{i+1}}{g_i}\exp\left[-\frac{(\epsilon_{i+1}-\epsilon_i)}{k_BT}\right]](/pictures/frwiki/50/2484702b34c60d1531ca30548fc34e19.png)
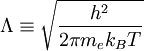
![\frac{n_e^2}{n-n_e} = \frac{2}{\Lambda^3}\frac{g_1}{g_0}\exp\left[\frac{-\epsilon}{k_BT}\right]](/pictures/frwiki/52/427932d7b2eda4f33f7bb24517ff820c.png)
Wikimedia Foundation. 2010.
