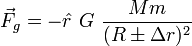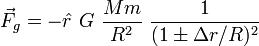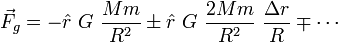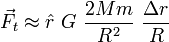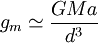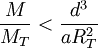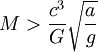- Effet de marée
-
Force de marée
 La comète Shoemaker-Levy 9 en 1994 après avoir été brisée par les forces de marée de Jupiter au cours d'un passage précédent, en 1992.
La comète Shoemaker-Levy 9 en 1994 après avoir été brisée par les forces de marée de Jupiter au cours d'un passage précédent, en 1992.
La force de marée est une conséquence de la non-uniformité de la force de gravitation exercée sur un corps par l'ensemble des astres qui l'entourent. Notamment, le côté d'un corps le plus près d'un astre subit une plus grande force que le côté le plus éloigné. C'est cette variation de la force de gravitation en deux points d'un même corps qui est appelée terme différentiel de marée ou plus simplement force de marée. Les forces de marée engendrent des contraintes sur les corps impliqués, ce qui les déforme ou peut même les briser : la limite de Roche est la distance entre deux corps à partir de laquelle le plus léger se désintègre.
Les forces de marée sont une manifestation du caractère non galiléen du référentiel géocentrique. Elles sont dues aux forces d'inertie (en l'occurrence une force d'inertie d'entraînement) agissant sur un corps étudié dans ce référentiel et se calculent en considérant le mouvement de rotation du centre de la Terre dans le référentiel héliocentrique.
Sommaire
Système Terre-Lune
Les marées océaniques sur la planète Terre
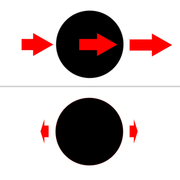
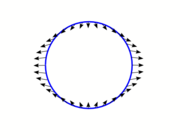 La force de gravitation de la Lune à la surface de la Terre diffère de l'effet moyen (sur le centre de la Terre), et est connu sous le nom de force génératrice des marées. Sur cette figure, la Lune est loin à gauche de la Terre ; à gauche, la Lune est au-dessus du point (i.e., au zénith), son attraction est plus forte, et elle s'oppose à l'attraction de la Terre ; à droite, la Lune est au nadir, son attraction est plus faible, ce qui s'oppose aussi à l'attraction de la Terre (en sens inverse). En haut et en bas de la figure, la Lune est à l'horizon, son attraction est dirigée légèrement vers le sol, donc sa force renforce l'attraction nette de la Terre.
La force de gravitation de la Lune à la surface de la Terre diffère de l'effet moyen (sur le centre de la Terre), et est connu sous le nom de force génératrice des marées. Sur cette figure, la Lune est loin à gauche de la Terre ; à gauche, la Lune est au-dessus du point (i.e., au zénith), son attraction est plus forte, et elle s'oppose à l'attraction de la Terre ; à droite, la Lune est au nadir, son attraction est plus faible, ce qui s'oppose aussi à l'attraction de la Terre (en sens inverse). En haut et en bas de la figure, la Lune est à l'horizon, son attraction est dirigée légèrement vers le sol, donc sa force renforce l'attraction nette de la Terre.
Les marées océaniques sont les grands mouvements des masses océaniques soumises à la gravitation lunaire et, dans une moindre mesure, celle du Soleil.
La force de gravitation exercée par un corps est une force proportionnelle à la masse de ce corps et à l'inverse du carré de la distance m/r² (pour la force exercée par la Lune sur la Terre, m est la masse de la Lune, r est la distance Terre-Lune). La force de marée étant un terme différentiel, elle est proportionnelle à la variation de la force de gravitation par rapport à la distance r, ce qui donne un effet proportionnel à m/r³. C'est cette proportionnalité qui explique que le Soleil, bien que beaucoup plus massif que la Lune, ait néanmoins un effet égal à seulement environ 45% de celui de la Lune car la distance Terre-Lune est bien plus petite que la distance Terre-Soleil.
Sous l'effet du mouvement relatif de la Lune par rapport à la Terre[1], la force de gravité qui est ressentie à la surface de la Terre varie continuellement. À ces changements, la masse liquide des océans se déforme pour retrouver son point d'équilibre. La modification est relativement faible parce que la Lune orbite relativement loin de la Terre et sa masse est assez faible. Néanmoins, sur une masse liquide et donc facilement déformable comme les océans, ce changement se traduit par une variation du niveau des eaux qui est connue sous le nom de marée.
L'amplitude théorique des marées océaniques est d'environ 1 mètre à l'équateur, mais leur valeur réelle diffère considérablement
- d'abord par un phénomène complexe de résonance. La période propre des océans est relativement longue, environ 30 heures (alors que celui de la croûte terrestre est d'environ 57 minutes). Cela veut dire que si la Lune disparaissait soudain, le niveau des océans oscillerait avec une période de 30 heures et une amplitude décroissant progressivement jusqu'à ce que l'énergie emmagasinée soit dissipée (cette valeur de 30 h est fonction uniquement de la gravité terrestre et de la profondeur moyenne des océans). Et la Lune stimule les océans avec une période d'environ 12,42 heures (la moitié de la période de rotation synodique de la Terre), inférieure à la période propre des masses d'eau, qui réagissent avec retard : le principal effet est que le retard des marées est, en moyenne, de six heures (c'est-à-dire que la marée basse se produit quand la Lune passe au zénith ou au nadir, un résultat tout à fait opposé à l'intuition commune)
- ensuite à cause de la topographie des lieux : avec une configuration en entonnoir (l'ensemble Manche / baie du mont Saint Michel étant l'un des exemple les plus fameux) l'effet de la marée est localement amplifié, inversement une mer fermée comme la Méditerranée connait des marées faibles.
Marées atmosphériques et terrestres
En plus des marées océaniques, il y a des marées atmosphériques ainsi que des marées terrestres, s'exerçant sur la masse rocheuse de la Terre. Les marées atmosphériques sont peu observables, noyées par les effets beaucoup plus importants dus à la météo d'une part et aux marées thermiques solaires d'autre part. La croûte terrestre, elle, se déforme régulièrement de manière peu perceptible en fonction des mouvements lunaires. L'amplitude des marées terrestres est d'environ 1,5 mètre à l'équateur, et elles sont en phase avec la Lune - ce qui fait qu'elles amplifient l'effet apparent des marées océaniques. Ce mouvement incessant s'associe à des phénomènes de stress et donc de fragilisation qui jouent un rôle à long terme dans le déclenchement de certains tremblements de terre. En revanche, quoi qu'en disent les magazines à sensation, même l'alignement de nombreuses planètes du système solaire n'a pas de vraies conséquences observables, et cela en raison de leur distance énorme à la Terre, dont le carré intervient en dénominateur.
De manière générale, on parle de forces de marée pour tous les corps qui subissent ce type de variation de la gravité locale à cause des mouvements d'un corps massif (de préférence sur une orbite à peu près circulaire). Ces forces sont généralement peu sensibles, mais dans un certain nombre de cas, elles peuvent prendre des proportions telles que l'impact en est observable plus facilement.
Traitement mathématique
Étant donné un champ gravitationnel extérieur donné, l'accélération de marée à un point d'un corps est obtenue par soustraction vectorielle de l'accélération au centre du corps de celle au point. La force de marée est la force qui correspond à cette accélération. Il est à noter que la seule force de gravitation tenue en compte pour ces calculs est celle entre les deux corps, donc la force extérieure ; le champ gravitationnel du corps lui-même n'est pas pertinent.
L'accélération de marée ne requiert pas de rotation ou que le corps soit en orbite. Par exemple, le corps peut être en chute libre en ligne droite, sous l'influence d'un champ gravitationnel et quand même être soumis à une accélération de marée (de plus, cette accélération varie elle-même).
Application de la loi universelle de la gravitation
Selon la loi universelle de la gravitation, une particule de masse m à une distance r du centre d'une sphere de masse M subit une force égale à :
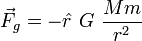 ,
,
où
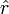 est le vecteur unitaire qui pointe dans la direction qui va à partir de M jusqu'à la particule m.
est le vecteur unitaire qui pointe dans la direction qui va à partir de M jusqu'à la particule m.On étend la description de m pour qu'il représente un petit corps sphérique avec un volume donné. Posons R, la distance inter-objet, c'est-à-dire du centre de M à celui de m et posons ∆r, le rayon de m. Par conséquent, les points sur la surface de m sont situés à une distance r = R ± ∆r du centre de R. On applique alors l'équation ci-haut et, en ignorant la contribution négligeable du la masse de m au champ gravitationnel, on obtient la force gravitationnelle en ces points :
Application de la série de Taylor
Le développement de 1/(1 + x)2 par la série de Taylor est 1 – 2x + 3x2 – ... Donc, on met en évidence le R du dénominateur pour obtenir :
et on applique le développement en série au résultat :
Le premier terme de la série est la force gravitationnelle telle qu'on la connaît traditionnellement. En général, le deuxième terme est beaucoup plus significatif que les suivants. Par conséquent, la force de marée s'exprime comme :
où dans F_t, l'indice t rappelle tide, ou marée en anglais.
Au-delà du système Terre-Lune
Europe (une des lunes de Jupiter) fait apparaître un nombre important de fissures à sa surface. Il est supposé qu'elles résultent des déformations continuelles que subit Europe à cause de sa révolution autour de Jupiter, la géante gazeuse. Parallèlement, le passage régulier d'Europe à proximité d'Io est considéré comme la source principale de son échauffement interne (qui fait de Io le seul corps non-terrestre sur lequel on ait observé un volcan actif).
À proprement parler, la force de marée est l'écart entre la gravitation observée en un lieu d'un corps (par exemple, sur la face visible de la Lune) et en un autre lieu du même corps (par exemple, sur la face cachée de la Lune). Tant que cet écart est faible au regard des forces de cohésion qui retiennent le corps lui-même, l'effet est faible ou nul. Tant que cet écart ne varie pas les contraintes sont statiques (et plus faciles à soutenir). La Lune, par exemple, parce qu'elle présente toujours la même face à la Terre subit une force de marée complètement statique. Elle en est légèrement déformée (elle n'est pas complètement sphérique). De plus, elle reste faible au regard de la cohésion du globe lunaire (elle ne s'en déforme pas continuellement contrairement aux océans terrestres qui subissent son influence).
Plus les masses mises en œuvre sont importantes, plus les effets sont importants (de façon linéaire). Plus les distances mises en œuvres sont faibles, plus les effets sont importants (en raison inverse du carré de la distance). Les astrophysiciens ont ainsi observé des couples stellaires (deux étoiles proches en rotation l'une autour de l'autre) qui résonnent sous les vibrations qu'elles s'imposent mutuellement.
Mais plus les masses sont importantes, plus les phénomènes deviennent difficiles à quantifier avec la théorie classique de la gravitation. On en arrive ainsi à des situations où les forces en jeu sont proprement gigantesques et les corrections dues à la relativité générale d'Albert Einstein ne peuvent plus être négligées. Toutefois, les phénomènes restent essentiellement les mêmes.
Échauffement dû aux forces de marées
L'échauffement dû aux forces de marées se produit en raison des frictions des marées : de l'énergie rotationnelle et orbitale est dissipée en énergie thermique au sein de la croûte des lunes et planètes impliquées. Io, une lune de Jupiter, est le corps le plus actif du système solaire. Les forces de marées déforment Io et chauffent l'intérieur de la lune. Des phénomènes similaires auraient entrainé la fusion de la glace dans certaines couches d'Europe, une autre lune de Jupiter.
Cas des trous noirs
Le cas le plus spectaculaire est celui d'un objet en orbite proche autour d'un trou noir stellaire. La masse proprement astronomique du trou noir et sa petite taille autorisent un corps (une étoile ou une planète) à s'en approcher beaucoup et alors la différence de force gravitationnelle entre les deux faces de l'objet est gigantesque. Cet écart est tel que tout corps un tant soit peu volumineux est déchiqueté par la force de marée. C'est ce qui explique le commentaire qui accompagne toujours les descriptions de ce qui arriverait à un vaisseau spatial qui plongerait dans un trou noir stellaire : il serait détruit par les forces de marée avant même d'en avoir atteint l'horizon.
Cependant, à l'extérieur du trou noir, l'effet diminue au fur et à mesure que sa masse augmente. Dans le cas d'un trou noir galactique, dont la masse se mesure en millions de masses solaires, le rayon de l'horizon est suffisamment grand pour que la force de marée à ses environs soit sans danger pour un être humain qui se trouverait là.
En effet, l'amplitude des effets de marées subi par un corps de taille a situé à une distance d d'une masse M s'écrit comme le produit du gradient du champ gravitationnel par la taille de l'objet, soit :
où G est la constante de Newton. Pour un être humain (où a vaut de l'ordre d'un mètre), la valeur maximale de gm supportable est de l'ordre de l'accélération de la pesanteur terrestre g (cela correspond à une situation où une personne suspendue par les mains serait lesté d'une masse de l'ordre de 100 kilos ; au-delà elle serait écartelée). Cela correspond donc à la contrainte :
où MT et RT correspondent à la masse et le rayon de la Terre. Pour un trou noir, la taille R de l'horizon est donnée approximativement par la formule
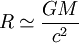 . Pour un observateur traversant l'horizon (d = R), la contrainte devient :
. Pour un observateur traversant l'horizon (d = R), la contrainte devient :soit de l'ordre de la centaine de milliers de masses solaires. Pour un trou noir plus massif comme un trou noir galactique, il est donc possible de passer l'horizon sans dommage.
Notes
- ↑ mouvement essentiellement dû à la rotation propre de la Terre en-dessous de la Lune, car la Lune ne tourne autour de la Terre qu'en 28 jours, alors que la Terre tourne sur elle-même sous la Lune en 24 heures
- ↑ (en) R. S. MacKay, J. D. Meiss, Hamiltonian Dynamical Systems: A Reprint Selection, CRC Press, 1987 (ISBN 0852742053), p. 36
Voir aussi
- Portail de la physique
- Portail de l’astronomie
Catégories : Gravitation | Marée
Wikimedia Foundation. 2010.