Effet Sagnac

L'effet Sagnac est un phénomène physique découvert par Georges Sagnac en 1913. C'est une asymétrie de la vitesse relative de signaux lumineux parcourant en sens inverse la circonférence d'un disque en rotation.

Sommaire 1 Introduction et présentation succincte 2 Présentation détaillée 2.1 Description du phénomène 2.2 Résultats expérimentaux 2.3 Universalité 2.4 Le problème de la lumière 3 Interprétation simpliste 4 L'addition des vitesses 5 Un problème plus compliqué qu'il n'y paraît 6 Résultats expérimentaux récents 7 Applications 8 Voir aussi 8.1 Articles connexes 8.2 Liens externes 8.3 Bibliographie

Introduction et présentation succincte

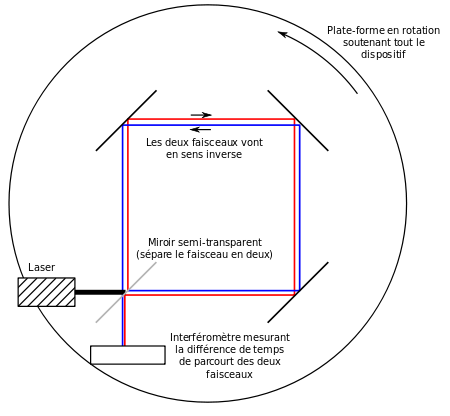
On appelle « Effet Sagnac » le décalage temporel de la réception de signaux lumineux « tournant en sens inverse » quand ils sont émis par un émetteur-récepteur fixé sur un disque tournant. En effet, si un émetteur placé sur un disque en rotation envoie deux signaux lumineux contraints de suivre la circonférence du disque, chacun dans un sens, les deux signaux reviennent à l'émetteur après un tour complet mais avec un léger décalage temporel qui dépend de la vitesse de rotation du disque. Ce décalage temporel entre les instants d'arrivée des deux signaux lumineux tournant en sens inverse est très facile à calculer.

Pour cela, le long de la circonférence d'un disque de rayon R tournant à la vitesse v = ωR (au niveau du rayon R) on fait tourner :

• un rayon lumineux dans le même sens que le disque (il tourne alors à la vitesse relative c-v par rapport à ce disque et en fait donc le tour en un temps 2πR / (c − v))
• un rayon lumineux dans le sens opposé à celui du disque (il tourne alors à la vitesse relative c+v par rapport à ce disque et en fait donc le tour en un temps 2πR / (c + v))

L'anisotropie de la vitesse relative de la lumière par rapport au disque tournant est mise en évidence par le décalage temporel δT (appelé effet Sagnac) entre les instants d'arrivée des deux signaux lumineux :

• δT = 2πR / (c − v) − 2πR / (c + v) pour un observateur inertiel
• pour un observateur tournant situé au rayon R.

Dans le cas où le signal lumineux se propage dans un milieu réfringent (par exemple une fibre optique faisant le tour du disque) avec une vitesse c'= c/n (où n>1 désigne l'indice de réfraction), on doit tenir compte du fait que, par rapport au référentiel inertiel R où tourne le disque, la vitesse c₂ du signal lumineux tournant dans le sens de rotation du disque et la vitesse c₁ du signal lumineux tournant en sens inverse ne valent plus c mais, conformément à la loi de composition relativiste des vitesses
c₁ = (c' + v) / (1 + c'v / c²) et c₂ = (c' − v) / (1 − c'v / c²). On a alors :

δT = 2πR / c₁ − 2πR / c₂

Une fois le calcul fait, on obtient le même résultat que ci-dessus (l'effet Sagnac ne dépend pas de l'indice de réfraction n).

On mesure ce décalage temporel par une expérience d'interférence entre les deux signaux lumineux (en leur point de réception sur le disque tournant). Ce décalage des instants d'arrivée des deux signaux lumineux (tournant en sens inverse le long de la circonférence du disque tournant) provoque en effet un décalage des franges d'interférence mettant ainsi en évidence l'anisotropie de la vitesse relative de la lumière par rapport au disque tournant.

Cet effet fut parfois considéré comme une mise en défaut de la relativité restreinte, en particulier par Sagnac lui-même mais aussi, encore récemment, par Franco Selleri et d'autres dans le courant des années 1990. En effet, ce décalage dans l'arrivée des signaux est constaté avec des signaux lumineux qui ont, dans le repère tournant, la même distance à parcourir (la circonférence du disque). La relativité restreinte nous dit que la vitesse de la lumière dans le vide est invariante. Cela semble mettre en évidence un désaccord avec la relativité.

En réalité, l'effet Sagnac s'explique parfaitement dans le cadre de la relativité restreinte. Elle peut conduire à des difficultés et à des paradoxes si on n'a pas bien compris que l'invariance de la vitesse relative de la lumière (et d'une façon plus générale, la symétrie des effets relativistes) concerne exclusivement les mouvements relatifs de translation à vitesse constante dans un espace-temps de Minkowski (et n'est valide que localement si on passe en relativité générale).

L'analyse plus détaillée de l'effet Sagnac présentée ci-dessous nécessite des outils plus élaborés que ceux utilisés habituellement en relativité restreinte. Une lecture superficielle de ce qui suit peut donc laisser croire que l'effet Sagnac est compliqué. Une bonne compréhension physique de cet effet est possible avec ce que l'on en a dit ci-dessus donc sans entrer dans les nombreux détails qui suivent. Cela suffit pour éliminer les erreurs d'interprétation de l'effet Sagnac dues à une mauvaise compréhension intuitive de la relativité ; en particulier l'idée erronée selon laquelle la réciprocité des effets de la relativité restreinte (contraction de Lorentz des distances, dilatation temporelle de Lorentz, isotropie de la vitesse de la lumière, relativité de la simultanéité) s'appliquerait globalement à tous les types de mouvements ou encore la confusion fréquente entre symétrie globale vis-à-vis des actions du groupe de Poincaré (applicable en relativité restreinte) et symétrie seulement locale (applicable en relativité générale).

Présentation détaillée

Description du phénomène

L'effet Sagnac consiste à émettre, en même temps et en sens inverse, deux signaux lumineux à l'aide d'un émetteur-récepteur fixé sur un disque tournant, en les contraignant à suivre la périphérie du disque tournant, puis à mesurer le décalage temporel entre les instants de réception de ces deux signaux sur l'émetteur-récepteur. Pour bien comprendre, il est utile de comparer ce cas à celui ou les deux signaux sont envoyés et reçus par un observateur O au repos dans le repère inertiel où tourne le disque.

Un observateur O immobile envoie deux signaux 1 et 2 autour d'un disque de rayon R en rotation à la vitesse angulaire ω. Chaque signal fait le tour du disque.

Pour cela, on peut utiliser des miroirs, des fibres optiques ou d'autres dispositifs.

Il existe bien d'autres configurations possibles, par exemple employant des fibres optiques, avec des sources en rotation ou pas et des détecteurs interférométriques en rotation ou pas. On peut aussi faire interférer les deux rayons sur l'anneau lui-même de manière à obtenir une onde stationnaire en utilisant deux faisceaux de fréquences légèrement différentes. Cela peut se faire automatiquement en intégrant la cavité laser dans le circuit et en renvoyant les faisceaux dans la cavité après un tour. Ces dispositifs à verrouillage de phase sont les plus précis.

Revenons à la disposition circulaire. Nous supposerons dans un premier temps que ce sont deux signaux lumineux se propageant à la vitesse c (comme dans le vide).

Pour le moment, la rotation du disque n'a pas d'importance. Les deux signaux partis simultanément de O reviennent, après un tour, en O en même temps.

Considérons maintenant un observateur O' situé en périphérie du disque et en rotation avec celui-ci. Nous choisissons O' pour qu'il soit en O au moment où les deux signaux sont émis.

Comme O' se déplace, lorsque les signaux se rencontrent en O, O' n'est plus au même endroit. O' va à la rencontre du signal 2 qui arrive en O' un peu plus tôt et il fuit le signal 1 qui arrive en O' un peu plus tard.

Voyons ce qui se passe dans le repère de O', c'est-à-dire du point de vue de O'.

Dans le repère de O', le disque n'est pas en rotation (O' est immobile dans son propre repère et il est solidaire du disque). Les deux signaux font le tour et se retrouvent en O' après un tour. Mais contrairement au cas de la première figure, comme nous venons de le voir, les deux signaux n'arrivent pas en même temps. Le signal 1 arrive après le signal 2. Pour O', le signal 2 est plus rapide que le signal 1. La vitesse apparente des signaux est anisotrope (différente selon le sens de rotation du signal).

L'emploi du terme "apparent" est important car ce qui est mesuré n'est pas directement une vitesse mais les temps de départ et d'arrivée des signaux (ou un déplacement des franges d'interférence dans le cas d'une mesure interférométrique). Nous n'avons pas mesuré la longueur du parcours. Bien sûr, il semble évident que cette longueur soit simplement la longueur du cercle. Mais en relativité restreinte ce n'est pas aussi simple ! Ce qui n'empêche pas de nombreux amateurs de relativité de faire cette confusion facile.

Voyons maintenant, en physique classique (non relativiste, c'est-à-dire en utilisant les transformations de Galilée), ce que valent ces vitesses apparentes et le décalage de temps d'arrivée des signaux.

La vitesse angulaire du signal lumineux est simplement c / R. Par conséquent, si on appelle t₁ et t₂ les temps mis par les signaux 1 et 2 pour rencontrer à nouveau O', nous avons :

Soit

Nous trouvons donc pour le décalage de temps d'arrivée des signaux en O' :

Si la vitesse angulaire du disque (ou ce qui revient au même du repère en rotation) est faible par rapport à la vitesse angulaire de la lumière (régime non relativiste), alors

où S est la surface du disque.

Pour calculer la vitesse apparente des signaux pour O' (dans son repère), il suffit de diviser la circonférence par le temps de parcours. Cela donne les vitesses apparentes des deux signaux :

Si l'on note V la vitesse tangentielle du disque (ou de O' ou du repère en rotation), on a :

On trouve que la vitesse, dans le repère de O', des deux signaux est :

où V est la vitesse de O' dans R (la vitesse tangentielle au disque).

Ce qui est, sommes toute, bien naturel puisque nous retrouvons l'addition des vitesses de Galilée.

Résultats expérimentaux

L'effet a d'abord été constaté et mesuré en analysant les franges d'interférences des signaux lumineux en O'. Depuis, l'utilisation de laser, d'horloges atomiques et d'autres dispositifs, permet d'autres mesures et en particulier la mesure directe du décalage temporel (la différence de temps d'arrivée des signaux en O') calculé ci-dessus.

En 1893 Sir Oliver Lodge proposa d'étudier les effets de la rotation de la terre avec un grand interféromètre. Puis, en 1897, il proposa d'utiliser des interféromètres sur un disque en rotation. L'effet fut théoriquement anticipé par Michelson en 1904. En 1913, Sagnac a vérifié ces prédictions en utilisant un interféromètre en rotation rapide. Il avait prédit les résultats ci-dessus dans le cadre de la physique classique. Ce fut aussi le premier résultat expérimental rapporté de ce qui fut nommé l'effet Sagnac.

Toutefois, cet effet fut détecté par Franz Harres en 1912 dans une expérience de Fizeau, mais il ne fut correctement interprété comme étant l'effet Sagnac qu'en 1914 par Harzer.

En 1925, Michelson et Gale mesurèrent la rotation de la terre grâce à un grand interféromètre.

Depuis les années soixante, des mesures de plus en plus précises ont pu être effectuées grâce à l'emploi des lasers.

Les gyrolasers Sagnac (des gyroscopes à laser exploitant l'effet Sagnac) sont couramment utilisés pour mesurer avec précision la rotation d'un dispositif (relativement à un repère inertiel).

Universalité

Les formules précédentes restent valables pour un signal à vitesse quelconque (à condition de remplacer c par la vitesse du signal, étant entendu que c'est la vitesse du signal mesurée dans le repère R).

Mais ce que l'on désire mesurer, ce n'est pas le décalage entre O et O' (la dernière formule avec les vitesses apparentes traduit simplement l'addition galiléenne des vitesses), mais l'éventuel décalage de deux signaux émis dans un repère en rotation (c'est-à-dire avec la vitesse des signaux mesurée par O', la vitesse « normale », mesurée localement, pas en la regardant faire un tour). On désire considérer ce qui se passe réellement dans ce genre de repère, indépendamment de ce que fait O.

Si on emploie autre chose que de la lumière dans le vide, il faut veiller à ce que ce soit O' qui envoie lui-même les signaux afin qu'ils aient localement (en principe) la même vitesse dans R' (comme c'est le cas de la lumière en relativité dont la vitesse est invariante), le repère de O'. Et pour la lumière, un milieu de propagation en rotation si sa vitesse dans ce milieu est inférieure à c (par exemple des fibres optiques fixées au disque, car dans ce cas la vitesse du milieu influence la vitesse du signal, comme dans le cas du son avec l'air, ce que l'on vérifie aisément en mesurant la vitesse du signal sur un aller-retour dans de l'eau en mouvement, comme dans l'expérience de Fizeau).

Mais si c'est O' qui envoie le signal, aucun décalage ne peut être prédit par la méthode précédente. Dans O', les deux signaux allant à même vitesse, comme on le voit sur la figure tracée dans le référentiel de O', les deux signaux arriveront en même temps (c'est pour O qu'ils seront décalés). Comme dans la figure ci-dessus, ils parcourent le même cercle à la même vitesse, même si c'est dans des sens différents, et ils doivent arriver en O' en même temps.

En réalité un décalage est bien constaté. Et, plus surprenant encore, le décalage (de temps) calculé précédemment est identique quelle que soit la nature du signal et sa vitesse. C'est ce que l'on appelle l'universalité de l'effet Sagnac.

Cet effet est donc difficile à expliquer en physique classique (avec les transformations de Galilée, c'est même impossible).

Déjà, en 1914, Harzer avait constaté que l'effet subsiste en présence de la réfraction, c'est-à-dire dans un milieu où la lumière va moins vite que c.

L'effet avec des signaux de « matière » fut vérifié plus tard :

• En 1965, Zimmermann et Mercerau utilisèrent des paires de Cooper.
• En 1984, Atwood utilisa des neutrons.
• En 1991, Riehle utilisa des atomes de calcium.
• Et en 1993, Hasselbach et Nicklaus utilisèrent des électrons.
• L'effet de la rotation terrestre avec des neutrons fut mesuré par Werner an 1979.

Le problème de la lumière

En plus du problème de l'universalité, en relativité restreinte un problème supplémentaire se pose. En effet, en relativité restreinte, la vitesse de la lumière dans le vide est invariante et isotrope. Or les raisonnements qui ont conduit aux vitesses apparentes dans ce qui précède sont qualitativement indépendants de la relativité (un facteur gamma pourrait intervenir, tout au plus). Le raisonnement effectué avec les signaux émis par O et le décalage observé par O' (car il s'est déplacé le temps que les signaux fassent le tour) ne semble pas dépendre de la relativité restreinte.

Rappelez-vous la figure plus haut et le raisonnement effectué :

Ce décalage est évident, inévitable. L'anisotropie de la vitesse de la lumière (émise par O) semble donc incontournable dans un repère tournant (celui de O'). Ennuyeux pour une théorie (la relativité restreinte) qui dit que la vitesse de la lumière est invariante et isotrope !

Ce fait a plusieurs fois été utilisé pour tenter de réfuter la relativité restreinte, même encore récemment, aussi bien par des amateurs de relativité que par des théoriciens ayant en principe des connaissances plus approfondies de la relativité restreinte.

En réalité l'effet Sagnac est compatible avec la relativité restreinte et l'isotropie de la vitesse de la lumière dans tout repère mais que la relativité restreinte prédit en plus l'universalité du phénomène.

La déduction des transformations de Lorentz est valable dans tout repère (y compris accéléré) mais uniquement de manière locale dans un repère accéléré (c'est-à-dire dans un voisinage infinitésimal de l'origine du repère et pendant une durée infinitésimale). La vitesse de la lumière est peut-être invariante et isotrope localement, mais qui dit que sur un tour complet cela reste vrai ? Évidemment vous devez certainement vous demander comment cela est possible, comment une vitesse invariante en tout point peut donner quelque chose de variable sur une distance finie (la moyenne d'une valeur constante est égale à cette valeur). Ou comment la même vitesse locale pourrait conduire à une vitesse globale différente selon le sens de parcours du disque (la circonférence ne dépend pas du sens dans lequel on considère le cercle). Il y a effectivement des choses bien étranges qui se passent et, par exemple, définir le repère en rotation de tout le disque pose de grosses difficultés.

Mais ne brûlons pas les étapes, avant d'attaquer le problème correctement, rigoureusement et dans toute sa généralité, présentons une dérivation relativiste "simpliste" ainsi qu'une série de paradoxes liés à l'effet Sagnac.

Interprétation simpliste

Dans cette section, l'effet Sagnac est interprété de façon simpliste dans un paradigme relativiste. Bien que cette interprétation mène à des résultats désastreux, elle a le mérite d'exposer plusieurs notions importantes.

Dans le référentiel R de O, les deux signaux arrivent sur O' avec un décalage Δt mesuré sur l'horloge de O. O', en mouvement, doit observer une dilatation du temps. Toutefois, ce n'est pas si simple car O' se déplace entre les deux réceptions des signaux. Sachant que le temps dépend aussi de la position, il faut utiliser les transformations de Lorentz.

Supposons que la vitesse de rotation du disque n'est pas trop grande pour pouvoir assimiler la trajectoire de O' (entre l'émission et les réceptions des signaux) à un segment de droite. Ainsi, l'utilisation des transformations de Lorentz semble être justifiée.

Les signaux seront reçus par O' (dans le repère R) aux coordonnées :

On peut alors appliquer les transformations de Lorentz :

Soit avec les coordonnées précédentes :

On trouve donc dans le repère R' de O' :

Le résultat trouvé, c'est-à-dire le décalage de temps d'arrivée des deux signaux sur O' dans R', est exactement la valeur approchée obtenue précédemment, à un facteur gamma près (alors que pour cette expression approchée, nous sommes partis de la valeur classique exacte). Habituellement, c'est plutôt l'inverse qui se produit (la formule relativiste redonne la formule classique en supposant gamma proche de 1, en négligeant les termes d'ordres supérieurs, proportionnels au carré de la vitesse, comme dans le cas de l'effet Doppler).

Pour calculer la vitesse du signal dans R', il faut connaître la longueur de la circonférence. A priori, ce n'est pas trivial, car dans R la contraction des longueurs ne s'applique pas de manière homogène selon le point considéré sur la circonférence (l'orientation de la vitesse varie avec l'angle).

Mais grâce à la symétrie par rotation, il y a plus simple. En effet, à cause de cette symétrie, dans R et R', un disque reste un disque. La géométrie reste inchangée (ce raisonnement est incorrect). Par conséquent la contraction doit être homogène. De plus, la circonférence étant forcément toujours tangente à la vitesse, la contraction de Lorentz est indépendante de l'angle (ce qui est contradictoire avec ce qui est écrit auparavant, mais de toute façon, une contraction variable, donnant une circonférence bizarre, ne ferait que donner un facteur correctif en plus du facteur gamma, cela ne changerait pas les conclusions).

Si le disque a le périmètre 2πR' dans R' (le disque est immobile dans ce repère, ne pas confondre les repères R et R' avec les rayons du disque dans ces deux repères R et R'), alors il aura une longueur plus courte d'un facteur gamma dans R. 2πR = 2πR' / γ. C'est-à-dire que dans R' la longueur parcourue est plus longue.

Comme la vitesse des signaux est obtenue en divisant cette longueur par le temps de parcours et comme les deux sont augmentés d'un facteur gamma, il y a compensation. Un petit calcul utilisant les transformations de Lorentz pour la position et les coordonnées temporelles ci-dessus montrent que les formules d'addition des vitesses trouvées dans le cas classique restent valables :

(où V = ωR est la vitesse au bord du disque, c'est-à-dire la vitesse angulaire fois le rayon, la vitesse angulaire étant le nombre de tours par seconde multiplié par deux pi).

Deux constatations s'imposent :

• Dans R' la vitesse de la lumière est anisotrope, ce qui est a priori en contradiction avec la relativité restreinte. Toutefois, celle-ci ayant été établie dans des repères inertiels et non en rotation, nous pouvons l'admettre dans un premier temps.
• L'aspect universel de l'effet Sagnac ne s'explique pas, car l'effet n'apparaît qu'avec une vitesse de la lumière anisotrope dans R' alors qu'avec des signaux quelconques ayant une vitesse bien précise (même inférieure à c) et isotrope dans R', l'effet Sagnac est observé en pratique.
  Et cet effet ne peut être dû à une anisotropie non détectée car si la vitesse du signal (inférieure à c) est isotrope dans R, et donc anisotrope dans R', il y a un écart bien supérieur à celui calculé plus haut.

Ces raisonnements simples, à la limite simplistes, conduisent à divers paradoxes, dont le paradoxe d'Ehrenfest et le paradoxe de Selleri.

L'addition des vitesses

Les formules précédentes donnent l'addition des vitesses avec la lumière. Mais qu'en est-il de l'addition des vitesses en général. Que vaut l'addition des vitesses sur la circonférence du disque ?

Soit deux observateurs O' et O" se déplaçant à V' et V''.

Un rayon lumineux se déplaçant dans le même sens a pour vitesse respectivement pour O' et O" :

Soit V''' la vitesse relative de O' et O". Un raisonnement identique à celui utilisé dans la présentation de l'effet Sagnac (en utilisant O" comme « signal » pour O et O') montre que

Donc

C'est-à-dire

La lumière obéit dans le repère en rotation à l'addition galiléenne des vitesses.

En effectuant un passage à la limite, il apparaît un paradoxe analogue à celui de Selleri : l'addition des vitesses devient galiléenne dans un repère inertiel.

Avec des arcs de cercles qui sont quasiment des segments de droite, et en utilisant un signal allant dans le sens approprié, il y a même la possibilité d'avoir des signaux allant plus vite que c entre deux points quelconques. Or, cela viole la causalité et conduit donc à des inconsistances en relativité restreinte.

L'addition galiléenne des vitesses est compatible avec un espace-temps euclidien mais pas avec un espace-temps de Minkowski qui conduit aux transformations de Lorentz. Ces relations sont incompatibles avec les effets relativistes qui sont pourtant observés !

Cette explication montre que la formule donnant la vitesse de la lumière dans un repère tournant est incompatible avec l'invariance de c dans un repère inertiel. Pourtant, nous sommes censés avoir déduit ces relations de la relativité en se basant sur l'invariance de c. Cela semble (en apparence) mener à une inconsistance non seulement de la relativité restreinte, mais des données expérimentales elles-mêmes.

Un problème plus compliqué qu'il n'y paraît

En plus des paradoxes soulevés dans les sections précédentes et du problème de l'universalité de l'effet Sagnac, récapitulons quelques remarques qui montrent que le raisonnement simpliste est faux ou, à tout le moins, qu'il doit être sérieusement mis en doute et que l'analyse de l'effet Sagnac en relativité restreinte nécessite un traitement plus rigoureux.

• Dans l'espace-temps les rayons lumineux ne suivent pas la même trajectoire.
  
  
  
  Même dans R les trajectoires sont différentes, bien que dans R, la situation des deux trajectoires soit totalement symétrique et aucun problème particulier ne se pose.
  Ce dessin peut être trompeur car en relativité restreinte l'espace-temps est de Minkowski et pas euclidien comme cette figure. Il faut donc faire attention.
• Dans R', il y a asymétrie de ces trajectoires à cause de la rotation. Cette asymétrie n'existe pas dans R. C'est la différence entre R et R'.
• On ne peut pas considérer la circonférence vue dans le repère R comme la longueur des trajectoires dans R', même en lui appliquant la contraction des longueurs, car on ne peut pas sans précaution séparer l'espace du temps (l'espace en relativité restreinte n'est pas absolu) et l'existence de deux trajectoires asymétriques dans l'espace-temps ne simplifie pas les choses.
  Dans le dessin, la partie spatiale est l'horizontale (la longueur des circonférences est indiquée), identique pour les deux trajectoires, mais, répétons-le, la figure « sur papier » obéit à la géométrie d'Euclide, tandis que l'espace-temps à l'étude est de Minkowski, compliqué ici par la rotation.
  Ce problème peut-être relié aux intervalles de type spatial. Cet intervalle n'ayant pas de signification physique (pas de lien causal), la longueur de l'intervalle n'est pas fixée a priori. Lui attribuer une valeur quelconque ou le considérer comme non invariant ne modifie pas la physique. C'est une simple considération mathématique. Ce n'est que des considérations en rapport avec le principe de relativité qui conduisent à la forme de l'intervalle invariant, y compris spatial, que nous connaissons. Si l'on ne tenait compte que des données physiques (l'invariance de la vitesse de la lumière dans le vide), nous aurions plus de liberté et même si les intervalles lumineux et temporels seraient toujours invariants, l'intervalle spatial pourrait être quelconque.
  La circonférence est la longueur d'une figure géométrique purement spatiale. Par conséquent, on ne peut pas, sans précaution, considérer que la longueur des trajectoires est numériquement égale à la circonférence. Il pourrait y avoir violation involontaire du principe de relativité.
  L'espace n'est pas absolu. La relativité restreinte nous enseigne que tout est relatif et que la physique doit se décrire par les relations entre observateurs et objets. Le choix du repère n'est là que pour donner des valeurs numériques aux variables. On ne peut pas considérer le dessin avec le cercle comme un cadre absolu qui permettrait de mesurer à coup sûr la longueur des trajectoires.
• Les rayons lumineux ne suivent pas les géodésiques (c'est-à-dire les chemins les plus courts).
  Appelons A et B les points où O' rencontre les deux signaux lumineux. Traçons les géodésiques dans R (une droite) et dans R'.
  
  
  
  Pourquoi la géodésique ne rejoint-elle pas B dans R' ? Parce que les deux évènements spatio-temporels A et B ne peuvent pas être joint par une géodésique lumineuse (la lumière se déplace beaucoup plus vite que O' et les deux ratent leur rencontre). Par conséquent, A et B sont confondus dans R' (puisque O' est immobile dans R'), mais la géodésique lumineuse, la ligne droite dans R, est vue comme courbe dans R'. Pour s'en convaicre, dessiner cette géodésique point par point à partir de celle dans R en tenant compte de la vitesse c et de la vitesse et de la rotation de O' (par exemple en utilisant du papier millimétré et une calculette).
  Les trajectoires lumineuses entre A et B (évènements spatio-temporels) ne sont pas des géodésiques lumineuses et ne sont donc pas les chemins les plus courts dans l'espace-temps. La lumière doit emprunter une trajectoire imposée grâce à des miroirs ou une fibre optique, justement à cause de cela.
  Étant donné l'asymétrie des trajectoires, on ne peut pas supposer, sans le vérifier, que ces deux trajectoires « allongées » ont la même longueur dans l'espace-temps. Quand on voit la géodésique dans R', ce n'est pas trivial.
  Les géodésiques sont les chemins les plus courts, par exemple dans un espace plat (une feuille de papier),elles forment le quadrillage de la feuille. Sur une sphère, ce sont des courbes (les méridiens, par exemple).
  Cette courbure de la géodésique montre que l'espace est courbe dans R'. Même en physique classique (espace euclidien), l'espace est courbe vu dans un repère accéléré. Mais cela est peu discuté, car :
  • On sait qu'on doit s'appuyer sur un espace de Minkowski, donc on préfère passer directement à des espaces courbes relativistes.
  • Si on reste dans la physique classique, galiléenne, on peut se passer de ces subtilités en raisonnant dans R pour la cinématique et en utilisant, dans R', des astuces du type « forces fictives » ou « dérives » (force centrifuge et force de Coriolis responsable du sens de rotation des cyclones et due à la rotation de la Terre). L'espace-temps euclidien autorise des facilités que l'on n'a pas avec l'espace-temps de Minkowski.
• La courbure d'une variété (une ligne, une surface, etc.) est une propriété locale intrinsèque. Par exemple, on ne peut faire disparaître la courbure d'une sphère en l'aplatissant : elle se déchire.
  Il ne faut pas la confondre avec la courbure extrinsèque imposée de l'extérieur, par exemple en roulant une feuille de papier en cylindre : cela ne modifie pas la feuille de papier, seulement la manière dont elle est vue.
  Dans la suite du texte, quand on parlera de courbure, ce sera toujours de courbure intrinsèque.
  Le paradoxe d'Ehrenfest a déjà présenté ce type d'espace courbe (espaces sphériques ou hyperboliques) où la géométrie n'est pas euclidienne.
  Or l'espace-temps de Minkowski est plat (les trajectoires les plus courtes sont des droites). Un changement d'observateur ne modifie pas la courbure de l'espace-temps. La courbure peut d'ailleurs s'exprimer de manière mathématiquement invariante pour tout observateur.
  L'espace-temps dans R' doit donc rester plat. Ce n'est qu'en relativité générale que l'espace-temps est considéré courbe. Par des raisonnements simples, en présence de la gravitation, l'espace-temps ne peut pas rester plat.
  Mais ici nous n'envisageons nullement la gravitation. Nous avons un repère inertiel R dans un espace-temps plat de Minkowski et un observateur O' qui suit une trajectoire courbe (un cercle).
  Mais avoir un espace-temps plat ne signifie pas que l'espace est plat. Les géodésiques étant courbes, on doit employer des coordonnées curvilignes. Et si l'on effectue une « coupe » dans l'espace-temps pour considérer une « tranche » d'espace (on considère tous les points simultanés dans un repère donné), cette tranche ne sera pas nécessairement plate.
  C'est vrai en géométrie euclidienne, la plus communément apprise : il est donc difficile d'imaginer qu'il puisse en être autrement. Mais en géométrie de Minkowski, on ne peut pas séparer l'espace et le temps de manière arbitraire. Le problème étant que ce sont toutes les coordonnées qui sont curvilignes, y compris le temps.
  
  
• Une analogie avec une autre expérience donne un indice sur l'origine de la difficulté.
  Plaçons O et O' sur un segment de droite terminé par des miroirs.
  
  
  
  Cette expérience est identique à celle de Sagnac sauf que les rayons lumineux font demi-tour sur des miroirs au lieu de faire le tour sur un cercle.
  Ici aussi O' va constater un décalage et une vitesse apparente (en utilisant la longueur du segment pour calculer la vitesse) anisotrope.
  La longueur des trajectoires, même pour ce qui est de l'espace seul, est différente aussi bien dans R que dans R', et les miroirs se déplacent par rapport à O'.
  Se pourrait-il que dans l'expérience Sagnac, il y ait un phénomène analogue ? Dans la figure ci-dessus, on pourrait demander à ce que les rayons lumineux fassent un aller-retour avec les deux miroirs, ce qui est équivalent à un tour sur le cercle. Dans ce cas, cette figure est la projection sur une droite de l'expérience de Sagnac.

L'effet Sagnac est indépendant du rayon de courbure et on peut faire tendre l'arc de cercle de O' vers un segment de droite.
Dans ce cas, on devrait aussi considérer que pour R', la longueur des trajectoires n'est pas la même.
Quel est l'équivalent du déplacement des miroirs par rapport à O' dans le cas de l'expérience de Sagnac ? En fait, les miroirs fixent la géométrie de la trajectoire des rayons lumineux. Dire que les miroirs changent, que les trajectoires changent ou que la géométrie décrite par ces trajectoires change revient au même. Le changement de géométrie a une cause physique : l'accélération centripète. Dans le cas de l'expérience de Sagnac, cela devrait se traduire par un changement dans la géométrie avec une symétrie par rotation. C'est un peu plus compliqué à étudier qu'une situation linéaire avec deux miroirs.

Résultats expérimentaux récents

Au lieu de mesurer la vitesse apparente des signaux, on peut tenter de mesurer la vitesse de la lumière localement, directement. Comme on le fait sans rotation.

Des expériences ont en effet été menées afin de déterminer s'il y avait une anisotropie dans un repère en rotation. En voici quelques-unes effectuées de différentes manières (sources et récepteurs en rotation ou immobiles, mesures sur un aller simple ou un aller-retour).

• Cialdea utilise deux laser multi-modes montés sur une table en rotation et regarde les variations de leur figure d'interférence lorsque la table est mise en rotation. Il obtient une limite supérieure à l'anisotropie de 0,9 m/s.
• Krisher utilise deux masers à hydrogène fixés au sol et séparés par un lien en fibre optique de 21 kilomètres et regarde les variations entre leur phase. Il obtient une limite supérieure à l'anisotropie de 100 m/s.
• Champeney utilise un amortisseur de Moessbauer en rotation et un détecteur fixe pour donner une limite supérieure à l'anisotropie de 3 m/s.
• Turner utilise une source en rotation et un détecteur de Moessbauer fixe pour donner une limite supérieure à l'anisotropie de 10 m/s.
• Gagnon, Torr, Kolen, et Chang ont effectué un test de l'anisotropie avec un guide d'onde. Leurs résultats négatifs sont cohérents avec la relativité restreinte.

Applications

Le gyrolaser utilisé comme gyromètre est une application directe de l'effet Sagnac.

Voir aussi

Articles connexes

• Paradoxe d'Ehrenfest
• Paradoxe de Selleri
• Synchronisation dans les repères tournants
• Calcul de l'effet Sagnac en relativité restreinte
• Géométrie de l'espace-temps dans les repères tournants
• paradoxe des jumeaux et l'effet Sagnac
• Espace compact en relativité
• Paradoxe des jumeaux dans les espaces compacts
• Relativité restreinte
• Relativité générale
• Principe de relativité
• Paradoxe des jumeaux

Liens externes

• Effet Sagnac et gyrolaser
• Modèle de Rindler
• Cours de Relativité Générale, d'après (en) Lectures notes on General Relativity de Dean M. Caroll, traduction et adaptation par Jacques Fric, avril 2002.
• (en) Guido Rizzi et Matteo Luca Ruggiero, The relativistic Sagnac effect : two derivations,
• (en) J. F. Pascual-Sanchez, A. San Miguel et F. Vicente, Isotropy of the velocity of light and the Sagnac effect
• Références aux données expérimentales sur la relativité

Bibliographie

Ouvrages généraux

• Jean Hladik, Pierre-Emmanuel Hladik, Le calcul tensoriel en physique, 3^e édition Dunod. ISBN 2100040715, ISBN 2225846537, ISBN 2225841446
• V. Ougarov, Théorie de la Relativité Restreinte, Deuxième Edition, Editions Mir, Moscou. Traduction française Editions Mir, 1979.
• Edgard Elbaz, Relativité Générale et Gravitation, Editions Ellipses-Marketing, 1986, ISBN 2729886516 (épuisé)
• Charles W.Misner, Kip S. Thorne et John Archibald Wheeler, Gravitation, W.H. Freeman and Company, New York. ISBN 0716703440

Articles

• Sagnac M.G., C.R. Acad. Sci. Paris, 157, 708,1410 (1913)
• Harres F., Ph.D. Thesis, University of Jena, Germany (1912)
• Harzer P., Astron. Nachr., 199, 377 (1914)
• Michelson A.A., Gale H.G., Astrophys. J., 61, 137 (1925)
• Chow W.W. et al., Rev. Mod. Phys., 57, 61 (1985)
• Vali V. and Shorthill R.W., Appl. Opt., 15, 1099 (1976)
• Stedman G.E., Rep. Prog. Phys., 60, 615 (1997)
• Zimmermann J.E. and Mercerau J.E., Phys. Rev. Lett., 14, 887 (1965)
• Atwood D.K. et al., Phys. Rev. Lett., 52, 1673 (1984)
• Riehle F. et al., Phys. Rev. Lett., 67, 177 (1991)
• Hasselbach F. and Nicklaus M., Phys. Rev. A, 48, 143 (1993)
• Werner S.A. et al., Phys. Rev. Lett., 42, 1103 (1979)
• Cialdea, Lett. Nuovo Cimento 4 (1972), p821.
• Krisher et al., Phys. Rev. D, 42, No. 2, pp. 731-734, (1990).
• Champeney et al, Phys. Lett. 7 (1963), p241. Champeney, Isaak and Khan, Proc. Physical Soc. 85, p583 (1965). Isaak et al, Phys. Bull. 21 (1970), p255.
• Turner and Hill, Phys. Rev. 134 (1964), B252.
• Gagnon, Torr, Kolen, and Chang, Phys. Rev. A38 no. 4 (1988), p1767.
• Anderson R., Bilger H.R. and Stedman G.E., Am. J. Phys., 62, 975 (1994).

Autres sources

• Bernard LINET,D.E.A. de Physique Théorique - Paris VI, Paris VII, Paris XI, ENS, X, 2003 - 2004, Notes de cours de Relativité Générale.

• Portail de la physique