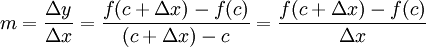- Droite secante
-
Droite sécante
En géométrie, la position relative de deux droites, ou d'une droite et d'une courbe, peut être qualifiée par l'adjectif sécante. Celui-ci vient du latin secare, qui signifie couper. En termes mathématiques, une droite est sécante à une autre droite, ou plus généralement à une courbe, quand elle a une intersection non vide avec celle-ci.
Pour effectuer l'étude d'une courbe au voisinage d'un de ses points P, il est utile de considérer les sécantes issues de P, c'est-à-dire les droites passant par P et un autre point Q de la courbe. C'est à partir de ces sécantes qu'est définie la notion de tangente à la courbe au point P : il s'agit de la limite, quand elle existe, des droites sécantes issues de P lorsque le deuxième point Q se rapproche de P le long de la courbe.
De ce fait, lorsque Q est suffisamment proche de P, la sécante peut être considérée comme une approximation de la tangente.
Dans le cas particulier de la courbe représentative d'une fonction numérique y=f(x), la pente de la tangente est la limite de la pente des sécantes, ce qui donne une interprétation géométrique de la dérivabilité d’une fonction.
Lien entre les notions de fonction sécante et de droite sécante
Considérons un réel θ. Dessinons une droite sécante au cercle unité (centré à l’origine) qui passe par l’origine et par le point (cos θ, sin θ), point du cercle dont le vecteur image fait un angle θ avec le vecteur directeur de l’axe des abscisses. La valeur absolue de la sécante trigonométrique de θ est égale à la longueur du segment de la droite sécante allant de l’origine jusqu’à la droite d’équation x = 1. Si le segment passe par le point (cos θ, sin θ), alors la sécante trigonométrique de θ est positive, s'il passe par le point antipodal, alors la sécante de θ est négative.
Approximation par une sécante
Considérons la courbe d’équation y = f(x) dans un système de coordonnées cartésiennes, et considérons un point P de coordonnées (c, f(c)), et un autre point Q de coordonnées (c + Δx, f(c + Δx)). Alors la pente m de la droite sécante, passant pas P et Q, est donnée par:
Le membre de droite de l’équation précédente est le rapport de Newton en c (ou taux d’accroissement). Lorsque Δx s’approche de zéro, ce rapport se rapproche du nombre dérivé f'(c), en supposant l’existence de la dérivée.
Voir aussi
- Portail de la géométrie
Catégories : Ligne droite | Courbe
Wikimedia Foundation. 2010.