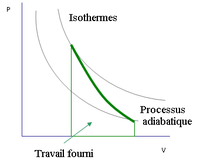
Adiabate

En thermodynamique, une transformation est dite adiabatique (du grec adiabatos, « qui ne peut être traversé ») si elle est effectuée sans qu'aucun transfert thermique n'intervienne entre le système étudié et le milieu extérieur. Un tel type de transformation induit une relation entre les différentes variables d'état du système considéré, comme la température, le volume ou la pression pour un gaz, ces quantités étant par ailleurs déjà reliées entre elles par une relation constitutive appelée équation d'état.

Sommaire 1 Mise en pratique de l'adiabaticité 2 Autre formulation 3 Utilisation 4 Voir aussi

Mise en pratique de l'adiabaticité

Le premier principe de la thermodynamique stipule que l'énergie est conservée. Pour un système physique interagissant avec un milieu extérieur, cela se traduit par le fait que la variation d'énergie interne au système est égale à la quantité d'énergie prise ou apportée par le milieu extérieur, que ce soit de l'énergie ordonnée (transfert d'énergie mécanique par le travail de forces appliquées sur le système, en l'occurrence les forces de pression pour un gaz), ou de l'énergie désordonnée sous forme d'énergie cinétique microscopique d'agitation thermique. Pour une transformation élémentaire (c'est-à-dire donnant lieu à une petite variation des paramètres décrivant le système), on a :

dU = δQ + δW ,

où

• dU représente la variation d'énergie interne,
• δQ est le transfert thermique élémentaire sur la transformation,
• δW est le travail élémentaire des forces agissant sur le système durant la transformation.

Dans le cas où l'évolution est réversible, le transfert thermique δQ correspond au produit de la température par la variation d'entropie. Pour un gaz parfait soumis uniquement à des forces de pression, ceci peut se réécrire en :

δQ = TdS = C_VdT + pdV .

Dans le cas d'une transformation qui serait adiabatique, en plus d'être réversible, le transfert thermique est nul ainsi que la variation d'entropie et on a :

δQ = 0 ,

D'où

0 = C_VdT + pdV ,

Pour un gaz parfait, si la transformation est réversible et adiabatique alors la relation suivante est vérifiée :

pV^γ = Cte ,

relation appelée loi de Laplace, où on définit l'indice adiabatique γ par

,

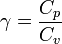avec

pV = nRT ,

où

nR = (C_p − C_v) ,

relation dite de Mayer.

Dans ces formules,

• C_p est la capacité calorifique du gaz à pression constante
• C_v est la capacité calorifique du gaz à volume constant
• γ est relié au nombre de degrés de liberté du gaz considéré. Pour un gaz parfait monoatomique, γ = 5 / 3, et pour un gaz diatomique (azote et oxygène, les principaux composants de l'air) dans les conditions usuelles de pression et de température γ = 7 / 5.

Pour que cette loi soit valable, γ doit être constant, donc C_p et C_v aussi du fait de la relation de Mayer (cf gaz parfait) classique. Cette relation est donc applicable pour la thermodynamique de Bose-Einstein ou de Fermi-Dirac.

Autre formulation

En remplaçant les termes, on obtient pour le changement de T (température) versus p dans un changement adiabatique réversible :

.

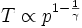L'exposant γ étant supérieur à 1, une transformation adiabatique réversible fait varier la pression dans le même sens que la température.

Utilisation

Un moteur thermique est un objet permettant d'échanger travail et chaleur avec un milieu extérieur. Cet échange se fait par un cycle répété de nombreuses fois. Dans ce cycle, se produit une série de transformations thermodynamiques. Parmi ces transformations, certaines sont adiabatiques. Par exemple, le cycle de Carnot correspond à un ensemble de deux transformations adiabatiques et deux transformations isothermes. Durant le cycle, le gaz subit une compression et une détente adiabatiques, ainsi qu'une compression et une détente isothermes.

Voir aussi

• compression adiabatique
  • Gradient thermique adiabatique
• isotherme, réversible, isentropique
• Entropie, gaz parfait
• Loi de Mariotte, Loi de Joule, Loi d'Avogadro.

• Portail de la physique