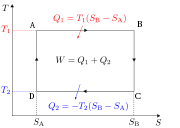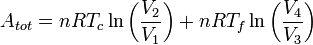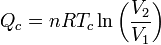Cycle De Carnot

Cycle De Carnot

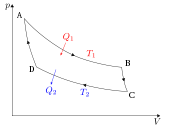Cycle de Carnot

Cycle de Carnot dans le diagramme de Clapeyron. AB : détente isotherme ; BC : détente adiabatique ; CD : compression isotherme ; DA : compression adiabatique.
Cycle de Carnot dans un diagramme température-entropie. AB : détente isotherme ; BC : détente adiabatique ; CD : compression isotherme ; DA : compression adiabatique.

Le cycle de Carnot est un cycle thermodynamique idéal constitué de quatre processus réversibles : une détente isotherme, une détente adiabatique (donc isentropique car réversible), une compression isotherme, et une compression adiabatique. C'est le cycle le plus efficace pour obtenir du travail à partir de deux sources de chaleur de températures constantes ; le cycle inverse est le moyen le plus efficace de transférer de la chaleur d'une source froide à une source chaude à partir d'une source de travail. L'efficacité des autres cycles et des machines réelles est comparé à celui du cycle de Carnot par le biais du rendement, un nombre sans dimension entre 0 (efficacité nulle) et 1 (efficacité du cycle de Carnot).

Il fut publié par Sadi Carnot en 1824 dans son unique ouvrage Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance et permit d'ouvrir la voie à la formulation du second principe de la thermodynamique.

Sommaire

Description du cycle

Carnot cherchait à faire un cycle avec la meilleure efficacité[1] possible. Ainsi chaque efficacité d'une machine thermodynamique peut être comparée avec l'efficacité du cycle de Carnot. Il sert de cycle de référence.

Le cycle est composé de 4 processus ( 2 isothermes et 2 adiabatiques réversibles) :

  • 1 : Compression adiabatique réversible
  • 2 : Détente isotherme
  • 3 : Détente adiabatique réversible
  • 4 : Compression isotherme

Le deuxième principe de la thermodynamique permet d'établir pour une transformation réversible (car le fluide est à la température de la source) l'égalité de Clausius-Carnot :

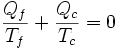
\frac{Q_f}{T_f}+\frac{Q_c}{T_c}=0

avec:

  • Qf transfert thermique avec la source froide (compté négativement).
  • Qc transfert thermique avec la source chaude (compté positivement).
  • Tf température absolue de la source froide.
  • Tc température absolue de la source chaude.

L'efficacité de Carnot

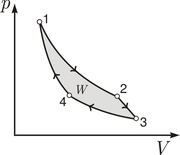Cycle de Carnot moteur d'un gaz parfait dans le diagramme de Clapeyron. 1-2 : adiabatique réversible ; 2-3 : isotherme réversible ; 3-4 : adiabatique réversible ; 4-1 : isotherme réversible. W est le travail total reçu par le système au cours d'un cycle et est représenté géométriquement par l'aire du cycle.

De nombreux systèmes thermodynamiques ont une efficacité définie à partir de celui du Cycle de Carnot, qui est un cycle purement théorique. En notant A l'aire géométrique de la transformation dans le diagramme de Clapeyron, c'est-à-dire l'opposé du travail W reçu par le système décrivant le cycle, on a :

A = − W = A1,2 + A2,3 + A3,4 + A4,1 et Qc = transfert thermique avec la source chaude, toutes les deux définies positives.

Donc pour chaque processus, en supposant que le fluide décrivant le cycle est un gaz parfait avec 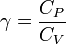\gamma = \frac{C_P}{C_V} et en notant T1 = T2 = Tc,T3 = T4 = Tf respectivement les températures des sources chaude et froide :

  • 1-2 :
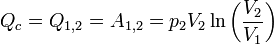
    • Q_c = Q_{1,2} = A_{1,2} = p_2 V_2 \ln\left(\frac{V_2}{V_1}\right)
    • ΔU1,2 = 0 car isotherme
  • 2-3 :
    • Q2,3 = 0 = A2,3 + ΔU2,3
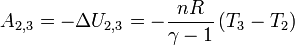
    • d'où : A_{2,3} = - \Delta U_{2,3} = - \frac{nR}{\gamma -1}\,(T_3 - T_2)
  • 3-4 :
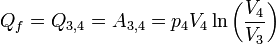
    • Q_f = Q_{3,4} = A_{3,4} = p_4 V_4 \ln\left(\frac{V_4}{V_3}\right)
    • ΔU3,4 = 0 car isotherme
  • 4-1 :
    • Q4,1 = 0 = A4,1 + ΔU4,1
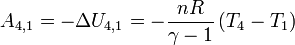
    • d'où : A_{4,1} = - \Delta U_{4,1} = - \frac{nR}{\gamma -1}\,(T_4 - T_1)

Donc, en tenant compte de 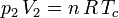p_2\,V_2 = n\,R\,T_c, on a :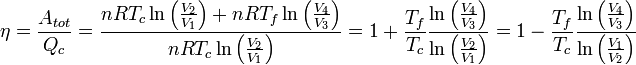

  • A_{tot} = nRT_c \ln\left(\frac{V_2}{V_1}\right) + nRT_f \ln\left( \frac{V_4}{V_3} \right)
  • Q_c = nRT_c \ln\left(\frac{V_2}{V_1}\right)

\eta = \frac{A_{tot}}{Q_c}=\frac{nRT_c \ln\left(\frac{V_2}{V_1}\right) + nRT_f \ln\left(\frac{V_4}{V_3}\right)}{nRT_c \ln\left(\frac{V_2}{V_1}\right)} = 1 + \frac{T_f}{T_c} \frac{\ln\left(\frac{V_4}{V_3}\right)}{\ln\left(\frac{V_2}{V_1}\right)} = 1 - \frac{T_f}{T_c} \frac{\ln\left(\frac{V_4}{V_3}\right)}{\ln\left(\frac{V_1}{V_2}\right)}

Nous avons également les formules de Laplace pour les processus processus isentropiques (donc ici les adiabatiques réversibles) :

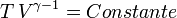T\,V^{\gamma -1} = Constante d'où :

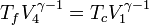
  • 4-1 : T_f V_4 ^{\gamma -1} = T_c V_1 ^{\gamma -1}
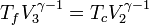
  • 2-3 : T_f V_3 ^{\gamma -1} = T_c V_2 ^{\gamma -1}

Et donc le rapport : 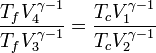\frac{T_f V_4 ^{\gamma -1}}{T_f V_3 ^{\gamma -1} } = \frac{T_c V_1 ^{\gamma -1}}{T_c V_2 ^{\gamma -1}} donc : 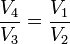\frac{V_4}{V_3} = \frac{V_1}{V_2} et finalement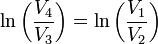 \ln\left(\frac{V_4}{V_3}\right) = \ln\left(\frac{V_1}{V_2}\right)

En incorporant ceci dans l'équation de l'efficacité on obtient :

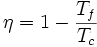
\eta = 1 - \frac{T_f}{T_c}

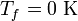
On voit donc qu'il est impossible d'obtenir une efficacité de 100%, même pour le cycle de Carnot moteur entièrement réversible, sauf pour le cas théorique T_f= 0\ \textrm{K}

Notes et références

  1. ↑ L'efficacité thermodynamique est le rapport de ce qui est récupéré sur ce qui a été dépensé. Elle est très souvent confondue avec le rendement qui est le rapport entre l'efficacité réelle et l'efficacité théorique maximale de la machine.

Articles connexes

Liens externes

Sur les autres projets Wikimedia :

  • Le cycle de Carnot
  • Réflexions sur la puissance motrice du feu, de Sadi Carnot (1824), extrait en ligne et commenté sur le site BibNum.
Cycles thermodynamiques
Cycles avec une
combustion externe
Cycles sans changement de phase
cycles de moteur à air chaud		 Cycle de Brayton • Cycle de Carnot • Cycle d'Ericsson • Cycle de Stirling • Cycle pseudo-Stirling ou Stirling adiabatique • Cycle de Stoddard • Cycle de Stirling-Vuilleumier
Cycles avec changement de phase Cycle de Kalina • Cycle de Rankine (inclut le cycle organique de Rankine) • Cycle régénératif • Cycle de Stirling biphasique •
Cycles avec une
combustion interne
Cycles mixtes
Cycle combiné • Cycle hybride à haut rendement • Cycle dual
Autres
Cycle de Claude • Cycle de Claude à double pression • Cycle de Fickett-Jacobs • Cycle de Gifford-McMahon • Cycle de Hirn • Cycle de Humphrey • Cycle de Siemens • Cycle de Hampson–Linde • Cycle de Linde à double pression • Cycle de Heylandt • Cycle de Kleemenko
  • Portail de la physique Portail de la physique
Ce document provient de « Cycle de Carnot ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Cycle De Carnot de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Cycle de carnot — dans le diagramme de Clapeyron. AB : détente isotherme ; BC : détente adiabatique ; CD : compression isotherme ; DA : compression adiabatique …   Wikipédia en Français

  • Cycle de Carnot — dans le diagramme de Clapeyron. AB : détente isotherme ; BC : détente adiabatique ; CD : compression isotherme ; DA : compression adiabatique …   Wikipédia en Français

  • cycle de Carnot — ● cycle de Carnot Cycle thermodynamique ditherme réversible, constitué de deux transformations isothermes et de deux transformations adiabatiques …   Encyclopédie Universelle

  • cycle de Carnot — Karno ciklas statusas T sritis fizika atitikmenys: angl. Carnot cycle vok. Carnot Kreisprozeß, m; Carnot Prozeß, m rus. цикл Карно, m pranc. cycle de Carnot, m …   Fizikos terminų žodynas

  • cycle de Carnot — Karno ciklas statusas T sritis Energetika apibrėžtis Grįžtamasis uždarasis ciklas, sudarytas iš dviejų izoterminių ir dviejų adiabatinių procesų. Vykstant šiam ciklui, gaunamas didžiausias teoriškai galimas šiluminio naudingumo koeficientas: η =… …   Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

  • cycle de Carnot — Karno ciklas statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. Carnot cycle vok. Karnot Prozess, m; Karnotscher Kreisprozess, m rus. цикл Карно, m pranc. cycle de… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • CYCLE — Une conception cyclique du temps a souvent été comprise par la pensée moderne comme la marque du primitivisme d’une culture ou le symptôme d’une régression archaïsante chez un sujet. Une telle conception, dans les deux cas, résulterait d’une… …   Encyclopédie Universelle

  • Cycle Combiné — L expression cycle combiné caractérise une production d énergie ou une centrale utilisant plus d’un cycle thermodynamique. Les moteurs thermiques transforment une partie de l’énergie fournie par le combustible en travail moteur pouvant ensuite… …   Wikipédia en Français

  • Cycle combine — Cycle combiné L expression cycle combiné caractérise une production d énergie ou une centrale utilisant plus d’un cycle thermodynamique. Les moteurs thermiques transforment une partie de l’énergie fournie par le combustible en travail moteur… …   Wikipédia en Français

  • Cycle Atkinson — Cycle d Atkinson Le cycle d Atkinson est un cycle thermodynamique utilisé dans un moteur à explosion. Il a été inventé par James Atkinson en 1882. Ce cycle, qui utilise une détente plus grande que la compression, améliore le rendement au prix d… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”