Diagramme de Bode

Le diagramme de Bode est un moyen de représenter le comportement fréquentiel d'un système. Il permet une résolution graphique simplifiée, en particulier pour l'étude des fonctions de transfert de systèmes analogiques. Il est utilisé pour les propriétés de marge de gain, marge de phase, gain continu, Bande passante, rejet des perturbations et stabilité des systèmes. Le diagramme de Bode doit son nom à Hendrik Wade Bode.

Sommaire

1 Définition
2 Tracé asymptotique des systèmes analogiques
- 2.1 Systèmes du premier ordre
  - 2.1.1 Passe-bas
  - 2.1.2 Passe-haut
- 2.2 Systèmes du second ordre
  - 2.2.1 Passe-Bas
  - 2.2.2 Passe-haut
3 Retour au cas général
4 Tracé des systèmes numériques
- 4.1 Limitation du domaine des pulsations
- 4.2 Transformation bilinéaire
5 Voir aussi

Définition

Le diagramme de Bode d'un système de réponse fréquentielle $T(j\omega)\$ est composé de deux tracés :

le gain (ou amplitude) en décibels (dB). Sa valeur est calculée à partir de $20\log_{10}{(|T(j\omega)|)}\$ .
la phase en degré, donnée par $\arg{(T(j\omega))}\$

L'échelle des pulsations est logarithmique et est exprimée en rad/s (radian par seconde). L'échelle logarithmique permet un tracé très lisible, car composé majoritairement de tronçons linéaires.

Diagramme de Bode du filtre passe-bas passif d'ordre 1. En pointillés rouges, l'approximation linéaire.

Tracé asymptotique des systèmes analogiques

Prenons une fonction de transfert quelconque qui s'écrit de la façon suivante :

$H(p)=\alpha p^q \frac{\prod_{k=1}^K \left(1+2\xi_k\frac{p}{\omega_k}+\left(\frac{p}{\omega_k}\right)^2\right)\prod_{l=1}^L \left(1+\frac{p}{\omega_l}\right)}{\prod_{m=1}^M \left(1+2\xi_m\frac{p}{\omega_m}+\left(\frac{p}{\omega_m}\right)^2\right)\prod_{n=1}^N \left(1+\frac{p}{\omega_n}\right)}$

où $\alpha \in \mathbb R\ ;\ q \in \mathbb Z\ ;\ \omega_k,\omega_l,\omega_m,\omega_n \in \mathbb R^*\ ;\ \xi_k,\xi_m \in \mathbb R\$

Bien qu'une fonction de transfert puisse s'écrire de plusieurs façons, c'est de la façon décrite ci-dessus qu'il faut les écrire :

les termes constants des polynômes élémentaires du premier et du second degré doivent valoir $1$ . Pour cela utiliser la constante $α$ .
Les termes en $p$ des polynômes élémentaires du premier et du second degré doivent être au numérateur. (voir la réécriture de la fonction Passe-haut ci-dessous)

On remarque que le module de $H(p)\$ est égal à la somme des modules des termes élémentaires en raison du logarithme. Il en va de même pour la phase, cette fois en raison de la fonction argument. C'est pourquoi on va dans un premier temps s'intéresser aux diagrammes de Bode des termes élémentaires.

Systèmes du premier ordre

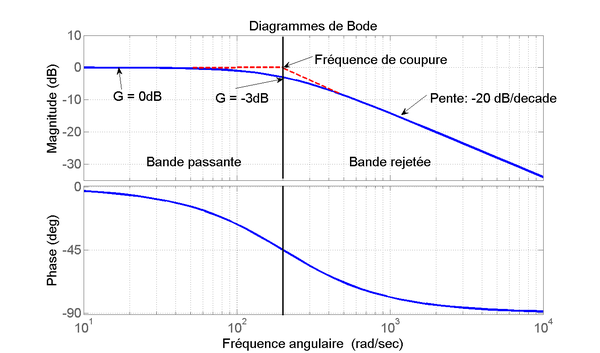
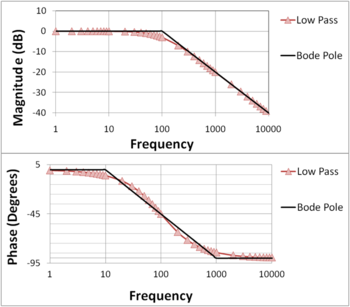
Passe-bas

Diagramme de Bode d'un filtre passe bas (système du 1er ordre)

Définition

Soit la fonction de transfert :

$H(p)=\frac{1}{1+\frac{p}{\omega_0}}\$

La pulsation $\omega_0\$ est appelée pulsation de coupure.

Tracé asymptotique

Pour $\omega \ll \omega_0,\ H(j\omega)\approx 1\$ donc $|H_{dB}(j\omega)|=0\$ et $\arg{(H(j\omega))}=0^\circ\$ .

Pour $\omega \gg \omega_0,\ H(j\omega)\approx -j\frac{\omega_0}{\omega}\$ donc $|H_{dB}(j\omega)|=-20\log_{10}(\omega)+20\log_{10}(\omega_0)\$ et $\arg{(H(j\omega))}=-90^\circ\$ .

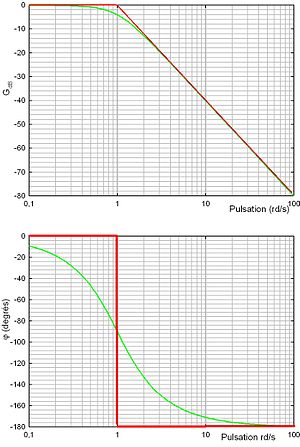
Dans un repère logarithmique, $|H_{dB}(j\omega)|\$ se traduit par une pente de -20dB/décade ou encore -6dB/octave. On parle également de pente -1. Le diagramme de Bode asymptotique du module se résume donc à deux tronçons linéaires.

Tracé réel

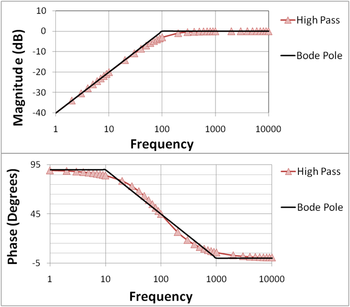
en $\omega_0\$ , $H(j\omega_0)=\frac{1}{1+j}$ soit $|H_{db}(j\omega_0)|=-20\log_{10}(\sqrt{2})=-10\log_{10}(2)$ : la courbe passe 3dB en dessous de l'asymptote.

Passe-haut

Diagramme de Bode d'un filtre passe haut (système du 1er ordre)

Soit la fonction de transfert :

$H(p)= \frac{1}{1+\frac{\omega_0}{p}} = \frac{\frac{p}{\omega_0}}{1+\frac{p}{\omega_0}}$

Le tracé s'obtient en prenant l'opposé du module en dB et de la phase du passe-bas.

Systèmes du second ordre

Passe-Bas

Définition

Un système du second ordre de type passe bas est caractérisé par une fonction de transfert du type :

$H(p)=\frac{H_0}{1+2\xi\frac{p}{\omega_0}+\left(\frac{p}{\omega_0}\right)^2}\$

$H 0$ est le gain statique. La pulsation $\omega_0\$ est appelée pulsation propre et $\xi\$ est l'amortissement.

Tracé asymptotique et Courbe réelle

Dans cette partie on prend le gain statique $H 0$ est égal à 1. Le tracé asymptotique dépend de la valeur de l'amortissement. On distingue trois cas :

$\xi\ >1$

Les pôles de la fonction de transfert sont réels (et négatifs pour des raisons de stabilité), et le système se décompose en un produit de deux fonctions de transfert du 1er ordre.Soit $p 1$ et $p 2$ les pôles réels de la fonction de transfert :

$H(p)=\frac{1}{1+2\xi\frac{p}{\omega_0}+\left(\frac{p}{\omega_0}\right)^2}=\frac{1}{\left(1-\frac{p}{p_1}\right)\left(1-\frac{p}{p_2}\right)}$

Diagramme de bode d'un système d'ordre deux avec un amortissement égal à 5.5 et

ω 0 = 1

.Le système se décompose alors sous la forme d'un produit de systèmes du premier ordre.

$\xi\ =1$

Les pôles sont réels, négatifs et égaux (pôle double). Si $p 0$ est un pôle double de la fonction de transfert, on obtient :

$H(p)=\frac{1}{1+2\xi\frac{p}{\omega_0}+\left(\frac{p}{\omega_0}\right)^2}=\frac{1}{\left(1+\frac{p}{\omega_0}\right)^2}$

Pour $\omega \ll \omega_0\ H(j\omega)\approx 1\$ donc $|H_{dB}(j\omega)|=0\$ et $\arg{(H(j\omega))}=0^\circ\$ .

Pour $\omega \gg \omega_0\ H(j\omega)\approx \left(\frac{\omega_0}{\omega}\right)^2\$ donc $|H_{dB}(j\omega)|=-40\log_{10}(\omega)+40\log_{10}(\omega_0)\$ et $\arg{(H(j\omega))}=-180^\circ\times \operatorname{signe(\omega_0\xi)}\$ .

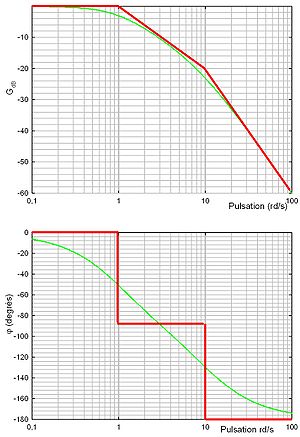
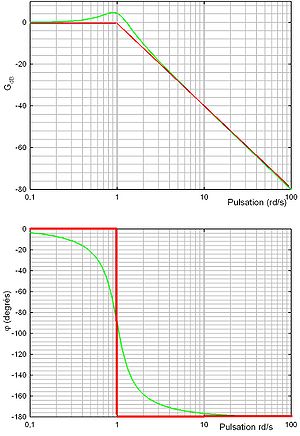
Dans un repère logarithmique, $|H_{dB}(j\omega)|\$ se traduit par une pente de -40dB/décade ou encore -12dB/octave. On parle également de pente -2. Le diagramme de Bode asymptotique du module se résume donc à deux tronçons linéaires.

$\xi\ <1$

Le diagramme asymptotique est le même que dans le cas précédent. Le pôles de la fonction de transfert sont complexes et conjugués, à partie réelle négative. Lorsque $\xi<\frac{\sqrt{2}}{2}\$ , le système présente une résonance. Le maximum du module de la fonction de transfert est alors $|H(j\omega)|_{max}=\frac{1}{2\xi\sqrt{1-\xi^2}}\$ en $\omega_R=\omega_0\sqrt{1-2\xi^2}\$ . La pulsation $ω R$ correspondant au maximum est donc toujours inférieure à $ω 0$ .

Diagramme de bode d'un système d'ordre deux avec un amortissement égal à 0.8 et

ω 0 = 1

Diagramme de bode d'un système d'ordre deux avec un amortissement égal à 0.3 et

ω 0 = 1

.Le système présente une surtension.

Passe-haut

$H(p)=\frac{(\frac{p}{\omega_0})^2}{1+2\xi\frac{p}{\omega_0}+\left(\frac{p}{\omega_0}\right)^2}\$

Le tracé s'obtient en prenant l'opposé du module en dB et de la phase du passe-bas.

Retour au cas général

Comme nous l'avons fait remarquer plus haut, on pourrait additionner tous les diagrammes de Bode des termes élémentaires pour obtenir le diagramme de la fonction de transfert $H(p)\$ .

Cependant, lorsque cette fonction de transfert est compliquée, il est plus facile de prendre en compte les contributions de chaque terme au fur et à mesure en faisant croître la pulsation $\omega\$ .

Au début, lorsque $\omega\rightarrow 0\$ , l'asymptote du module est une droite de pente q (q*20dB/Décade) et la phase est constante à $q \times 90^\circ\$ . Par la suite, à chaque fois que l'on rencontre une pulsation , on modifie le tracé selon la procédure suivante :

Pour $\omega=\omega_k\$ on rajoute +2 à la pente du module (+40dB/Décade) et $180^\circ\times \operatorname{signe(\omega_k\xi_k)}\$ à la phase.
Pour $\omega=\omega_l\$ on rajoute +1 à la pente du module (+20dB/Décade) et $90^\circ \times \operatorname{signe(\omega_l)}\$ à la phase.
Pour $\omega=\omega_m\$ on rajoute -2 à la pente du module (-40dB/Décade) et $-180^\circ \times \operatorname{signe(\omega_m\xi_m)}\$ à la phase.
Pour $\omega=\omega_n\$ on rajoute -1 à la pente du module (-20dB/Décade) et $-90^\circ \times \operatorname{signe(\omega_n)}\$ à la phase.

Tracé des systèmes numériques

Limitation du domaine des pulsations

Nous disposons cette fois d'une fonction de transfert $G(z)=\mathcal{Z}\{g(n)\}\$ d'un système discret.

Pour obtenir son diagramme de Bode, il faut évaluer la fonction sur le cercle unité.

Autrement dit, $z=e^{2\pi j\nu} \$ avec $\nu \in \left[0;\frac{1}{2}\right]$ (on obtient le cercle complet par symétrie).

Si le système discret a été obtenu à partir de l'échantillonnage à la période T d'un système continu , alors $z=e^{j\omega T} \$ avec $\omega \in \left[0;\frac{\pi}{T}\right]$ .

De plus, les relations $|G(z)|_{z=e^{2\pi j\nu}}\$ et $\operatorname{arg(G(z)_{z=e^{2\pi j\nu}})}\$ ne sont pas rationnelles en $\nu\$ . Par conséquence, l'étude du tracé est compliquée et nécessite des moyens informatiques.

Transformation bilinéaire

Cependant, il existe une application permettant de se ramener au cas continu :

$z=\frac{\frac{2}{T}+w}{\frac{2}{T}-w}\$

ou la fonction réciproque $w=\frac{2}{T}\frac{z-1}{z+1}\$

Il s'agit d'une transformée de Möbius.

Cette transformation fait correspondre l'axe imaginaire $w=j\Omega\$ du domaine continu avec le cercle unité $z=e^{j\omega T}\$ du domaine discret avec $\omega=\frac{2}{T}\operatorname{arctan \left(\frac{T \Omega}{2}\right)}\$ .

Or, lorsque $\omega T\ll 1$ , on a $\omega\approx\Omega\$ , auquel cas on se retrouve dans le cas continu d'une fraction rationnelle à étudier. On peut alors se ramener à une étude classique des systèmes analogiques sur $\omega \in \left[0;\frac{\pi}{T}\right]$ en sachant que les valeurs du diagramme près de $\omega= \frac{\pi}{T}\$ sont entachées d'une erreur.

Voir aussi

Sur les autres projets Wikimedia :

« Diagramme de Bode », sur Wikiversity (communauté pédagogique libre)

v · Électromagnétisme • Électricité • Électronique • Électrotechnique • Électrochimie • Automatique • Traitement du signal
Régulateurs : régulateur PID • Commande prédictive • Commande optimale • contrôleur flou
Types de stabilité : Stabilité de Lyapunov • Stabilité asymptotique • Stabilité EBSB
Représentations mathématiques : Représentation d'état • Fonction de transfert • Transformée en Z • Transformée de Laplace
Représentations graphiques : Diagramme de Nyquist • Diagramme de Bode • Diagramme de Black

Portail de l’électricité et de l’électronique

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Diagramme de Bode de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Diagramme De Bode — Le diagramme de Bode est un moyen de représenter le comportement fréquentiel d un système. Il permet une résolution graphique simplifiée, en particulier pour l étude des fonctions de transfert de systèmes analogiques. Il est utilisé pour les… … Wikipédia en Français
Diagramme de bode — Le diagramme de Bode est un moyen de représenter le comportement fréquentiel d un système. Il permet une résolution graphique simplifiée, en particulier pour l étude des fonctions de transfert de systèmes analogiques. Il est utilisé pour les… … Wikipédia en Français
diagramme de Bode — Bode diagrama statusas T sritis automatika atitikmenys: angl. Bode diagram; response/frequency diagram vok. Bode Diagramm, n; Frequenzgang, m rus. диаграмма Боде, f pranc. diagramme de Bode, m ryšiai: sinonimas – Bode diagrama … Automatikos terminų žodynas
Diagramme De Nyquist — Pour le théoricien de l informatique, voir Harry Nyquist. Le diagramme de Nyquist est un graphe utilisé en automatique pour évaluer la stabilité d un système en boucle fermée. Il représente, dans le plan complexe, la réponse harmonique du… … Wikipédia en Français
Diagramme de nyquist — Pour le théoricien de l informatique, voir Harry Nyquist. Le diagramme de Nyquist est un graphe utilisé en automatique pour évaluer la stabilité d un système en boucle fermée. Il représente, dans le plan complexe, la réponse harmonique du… … Wikipédia en Français
Diagramme de Nichols — Diagramme de Black Diagramme de Black. Le diagramme de Black est un graphe utilisé en automatique pour étudier un système. Il représente le gain en décibels (donc selon une échelle logarithmique) en fonction de la phase. Ce diagramme combine en… … Wikipédia en Français
Diagramme de Black — Diagramme de Black. Le diagramme de Black est un graphe utilisé en automatique pour étudier un système. Il représente le gain en décibels (donc selon une échelle logarithmique) en fonction de la phase. Ce diagramme combine en un les deux… … Wikipédia en Français
Bode diagram — Bode diagrama statusas T sritis automatika atitikmenys: angl. Bode diagram; response/frequency diagram vok. Bode Diagramm, n; Frequenzgang, m rus. диаграмма Боде, f pranc. diagramme de Bode, m ryšiai: sinonimas – Bode diagrama … Automatikos terminų žodynas
Bode diagrama — statusas T sritis automatika atitikmenys: angl. Bode diagram; response/frequency diagram vok. Bode Diagramm, n; Frequenzgang, m rus. диаграмма Боде, f pranc. diagramme de Bode, m ryšiai: sinonimas – Bode diagrama … Automatikos terminų žodynas
Bode-Diagramm — Bode diagrama statusas T sritis automatika atitikmenys: angl. Bode diagram; response/frequency diagram vok. Bode Diagramm, n; Frequenzgang, m rus. диаграмма Боде, f pranc. diagramme de Bode, m ryšiai: sinonimas – Bode diagrama … Automatikos terminų žodynas

Dictionnaires et Encyclopédies sur 'Academic'

Diagramme de Bode

Sommaire

Définition