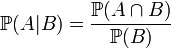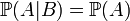Densité de probabilité conditionnelle

Densité de probabilité conditionnelle

Probabilité conditionnelle

La notion de probabilité conditionnelle permet de tenir compte dans une prévision d'une information complémentaire. Par exemple, si je tire au hasard une carte d'un jeu, j'estime naturellement à une chance sur quatre la probabilité d'obtenir un cœur ; mais si j'aperçois un reflet rouge sur la table, je corrige mon estimation à une chance sur deux. Cette seconde estimation correspond à la probabilité d'obtenir un cœur sachant que la carte est rouge. Elle est conditionnée par la couleur de la carte ; donc, conditionnelle.

La pratique n'est cependant pas toujours aisée, comme le montrent certains paradoxes tels que le paradoxe des deux enfants, le paradoxe des deux enveloppes, le paradoxe des trois pièces de monnaie et le paradoxe des prisonniers. D'où la nécessité d'une définition rigoureuse.


Sommaire

Définition

En théorie des probabilités, la probabilité conditionnelle d'un événement A, sachant qu'un autre événement B de probabilité non nulle s'est réalisé (ou probabilité de A, sachant B) est le nombre noté 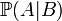\mathbb{P}(A|B) défini par :

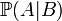\mathbb{P}(A|B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}

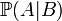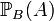Le réel \mathbb{P}(A|B) se lit « probabilité de A, sachant B ». \mathbb{P}(A|B) se note aussi parfois \mathbb{P}_B(A).

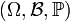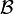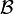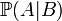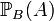Mathématiquement, soient \left(\Omega, \mathcal B, \mathbb{P}\right), un espace probabilisé et B un événement de la tribu \mathcal B de probabilité non nulle (non quasi-impossible). À tout événement A de \mathcal B, nous associons le nombre noté \mathbb{P}(A|B) ou \mathbb{P}_B(A) défini par:

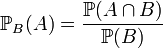\mathbb{P}_B(A) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}.

Nous pourrions vérifier que l'application 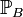\mathbb{P}_B définie par 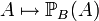A\mapsto \mathbb{P}_B(A) est une probabilité.

Si A et B sont indépendants alors:

\mathbb{P}(A|B) = \mathbb{P}(A)

Espérance conditionnelle

Article détaillé : Espérance conditionnelle.

Soit 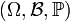\left(\Omega, \mathcal B, \mathbb{P}\right) un espace probabilisé, X une variable aléatoire réelle intégrable et B un évènement. On appelle espérance conditionnelle:


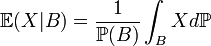
\mathbb{E}(X|B)=\frac{1}{\mathbb{P}(B)}\int_B X d\mathbb{P}

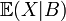\mathbb{E}(X|B) est l'espérance de X sachant que B s'est réalisé.

Densité conditionnelle

Soit 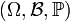\left(\Omega, \mathcal B, \mathbb{P}\right), Soit X et Y deux variables aléatoires de loi jointe f(x,y). Soit y0 tel que 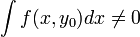\int f(x,y_0) dx \neq 0. On appelle densité conditionnelle la loi: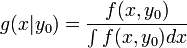

g(x|y_0)= \frac{ f(x,y_0) }{\int f(x,y_0) dx }

Articles connexes

  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques
Ce document provient de « Probabilit%C3%A9 conditionnelle ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Densité de probabilité conditionnelle de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Probabilite conditionnelle — Probabilité conditionnelle La notion de probabilité conditionnelle permet de tenir compte dans une prévision d une information complémentaire. Par exemple, si je tire au hasard une carte d un jeu, j estime naturellement à une chance sur quatre la …   Wikipédia en Français

  • Probabilité conditionnelle — La notion de probabilité conditionnelle permet de tenir compte dans une prévision d une information complémentaire. Par exemple, si je tire au hasard une carte d un jeu, j estime naturellement à une chance sur quatre la probabilité d obtenir un… …   Wikipédia en Français

  • Densité jointe — Loi de probabilité à plusieurs variables Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées… …   Wikipédia en Français

  • Probabilité bayésienne — Théorème de Bayes Le théorème de Bayes est un résultat de base en théorie des probabilités, issu des travaux du révérend Thomas Bayes et retrouvé ensuite indépendamment par Laplace. Dans son unique article, Bayes cherchait à déterminer ce que… …   Wikipédia en Français

  • Loi de probabilité à plusieurs variables — Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées fonctionnellement, cela introduit la notion de loi de …   Wikipédia en Français

  • Loi De Probabilité À Plusieurs Variables — Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées fonctionnellement, cela introduit la notion de loi de …   Wikipédia en Français

  • Loi de probabilite a plusieurs variables — Loi de probabilité à plusieurs variables Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées… …   Wikipédia en Français

  • Distribution conditionnelle — Probabilité conditionnelle La notion de probabilité conditionnelle permet de tenir compte dans une prévision d une information complémentaire. Par exemple, si je tire au hasard une carte d un jeu, j estime naturellement à une chance sur quatre la …   Wikipédia en Français

  • Fonction de répartition conditionnelle — Probabilité conditionnelle La notion de probabilité conditionnelle permet de tenir compte dans une prévision d une information complémentaire. Par exemple, si je tire au hasard une carte d un jeu, j estime naturellement à une chance sur quatre la …   Wikipédia en Français

  • Loi jointe — Loi de probabilité à plusieurs variables Dans certains problèmes interviennent simultanément plusieurs variables aléatoires. Mis à part les cas particuliers de variables indépendantes (notion définie ci dessous) et de variables liées… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”