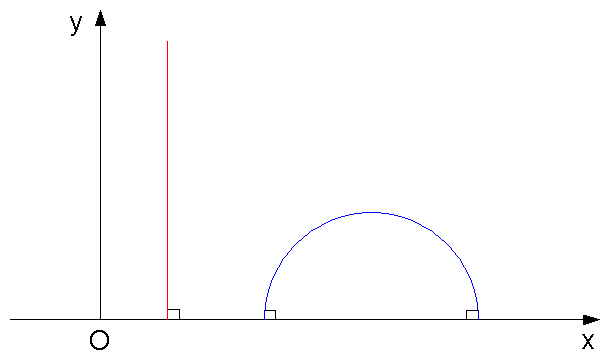
Demi-plan de poincaré

Demi-plan de poincaré

Demi-plan de Poincaré

Le demi-plan de Poincaré est un sous-ensemble des nombres complexes. Il a permis au mathématicien français Henri Poincaré d'éclairer les travaux du Russe Nicolaï Lobatchevski.

Sommaire

Le demi-plan de Poincaré (1882)

Le demi-plan de Poincaré est formé par les nombres complexes de partie imaginaire strictement positive. Il fournit un exemple de géométrie non euclidienne, plus précisément de géométrie hyperbolique.

Géométrie

On considère le demi-plan supérieur :

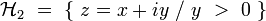
\mathcal{H}_2 \ = \ \left\{ \ z = x + i y \ / \ y \ > \ 0 \ \right\}

Métrique

On munit le demi-plan supérieur de la métrique :

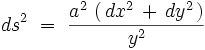
ds^2 \ = \ \frac{a^2 \, \left( \, dx^2 \, + \, dy^2 \, \right)}{y^2}

Cette métrique possède une courbure scalaire constante négative :

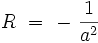
R \ = \ - \ \frac{1}{a^2}

On se ramène usuellement au cas d'une courbure unité, c’est-à-dire qu'on choisi : a = 1 pour simplifier les équations.

Géodésiques

Les géodésiques sont les demi-droites (au sens euclidien) verticales : x = cte (en rouge) et les demi-cercles (au sens euclidien) perpendiculaires à l'axe des abscisses  : y = 0 (en bleu) :

Geodes.GIF

On pourra consulter le site du mathématicien Andrew G. Bennett (université du Kansas) qui contient 3 applets java sur les géodésiques, les cercles hyperboliques et les triangles hyperboliques.

Homographies

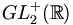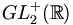Les matrices de GL_2^+(\mathbb R) agissent sur cet espace, par homographies [1]. Plus précisément, soit g un élément de GL_2^+(\mathbb R) :

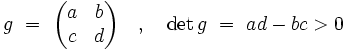
g \ = \ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \quad , \quad \mathrm{det} \, g \ = \ ad - bc > 0

Son action sur un point z du demi-plan est donnée par :

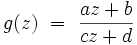
g(z) \ = \ \frac{az+b}{cz+d}

Groupes Fuchiens

Formes automorphes

Dynamique chaotique

Le flot géodésique sur une variété riemannienne à courbure négative est le prototype de système dynamique à temps continu le plus chaotique qui soit, une propriété remarquée dès 1898 par Hadamard[2]. On sait aujourd'hui que ce flot est, par ordre croissant d'irrégularités[3],[4] :

  • ergodique
  • mélangeant (« mixing »)
  • K-système (Anosov)
  • C-système = bernouillien[5].

Lire aussi : Chaos on the pseudosphere[6], Hyperbolic geometry in two dimensions and trace formulas[7], Quantum and classical properties of some billiards on the hyperbolic plane[8].

Liens

Bibliographie

Ouvrages de mathématiques

Géométrie

  • John Stillwell ; Geometry of Surfaces, Universitext, Springer-Verlag (1992), ISBN 0-387-97743-0.
  • Birger Iversen ; Hyperbolic Geometry, London Mathematical Society Student Texts 25, Cambridge University Press (1992), ISBN 0-521-43528-5.
  • Toshitsune Miyake ; Modular forms, Springer-Verlag (1989), ISBN 0-387-50268-8. Attention, ce n'est pas un livre pour débutant !

Chaos

  • Jacques Hadamard ; Les surfaces à courbures opposées et leurs lignes géodésiques, Journal de Mathématiques Pures & Appliquées 4 (1898) 27.
  • Pierre Pansu ; Le flot géodésique des variétés Riemanniennes à courbure négative, Séminaire Bourbaki 738 (1991) publié dans : Astérisque 201-203 (1991) 269-298.
  • Donald S. Ornstein & Benjamin Weiss ; Geodesic flows are Bernouillians, Isreal Journal of Mathematics 14 (1973) 184.
  • Vladimir Arnold & André Avez ; Ergodic problems of classical mechanics, Advanced Book Classics, Addison-Wesley (1988).

Références pour physiciens théoriciens

  • Nandor Balasz & André Voros ; Chaos on the pseudosphere, Physics Report 143 (1986) 109.
  • Yves Colin de Verdière ; Hyperbolic geometry in two dimensions and trace formulas, dans : Marie-Joya Giannoni, André Voros & Jean Zinn-Justin (éditeurs) ; Chaos & Quantum Physics, Proceeedings de l'École d'Été de Physique Théorique des Houches (1989) Session LII, North-Holland (1991), ISBN 0-444-89277-X.
  • Charles Schmit ; Quantum and classical properties of some billiards on the hyperbolic plane, dans : Marie-Joya Giannoni, André Voros & Jean Zinn-Justin (éditeurs) ; Chaos & Quantum Physics, Proceeedings de l'École d'Été de Physique Théorique des Houches (1989) Session LII, North-Holland (1991), ISBN 0-444-89277-X.

Notes

  1. ↑ Le groupe 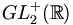GL_2^+(\mathbb R) est le sous-groupe de 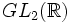GL_2(\mathbb R) formé par les matrices de déterminant positif.
  2. ↑ Jacques Hadamard ; Les surfaces à courbures opposées et leurs lignes géodésiques, Journal de Mathématiques Pures & Appliquées 4 (1898) 27.
  3. ↑ Vladimir Arnold & André Avez ; Ergodic problems of classical mechanics, Advanced Book Classics, Addison-Wesley (1988).
  4. ↑ Pierre Pansu ; Le flot géodésique des variétés Riemanniennes à courbure négative, Séminaire Bourbaki 738 (1991) publié dans : Astérisque 201-203 (1991) 269-298.
  5. ↑ Donald S. Ornstein & Benjamin Weiss ; Geodesic flows are Bernouillians, Isreal Journal of Mathematics 14 (1973) 184.
  6. ↑ Nandor Balasz & André Voros ; Chaos on the pseudosphere, Physics Report 143 (1986) 109.
  7. ↑ Yves Colin de Verdière ; Hyperbolic geometry in two dimensions and trace formulas, dans : Marie-Joya Giannoni, André Voros & Jean Zinn-Justin (éditeurs) ; Chaos & Quantum Physics, Proceeedings de l'École d'Été de Physique Théorique des Houches (1989) Session LII, North-Holland (1991), ISBN 0-444-89277-X.
  8. ↑ Charles Schmit ; Quantum and classical properties of some billiards on the hyperbolic plane, dans : Marie-Joya Giannoni, André Voros & Jean Zinn-Justin (éditeurs) ; Chaos & Quantum Physics, Proceeedings de l'École d'Été de Physique Théorique des Houches (1989) Session LII, North-Holland (1991), ISBN 0-444-89277-X.
  • Portail des mathématiques Portail des mathématiques
  • Portail de la physique Portail de la physique
Ce document provient de « Demi-plan de Poincar%C3%A9 ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Demi-plan de poincaré de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Demi-plan De Poincaré — Le demi plan de Poincaré est un sous ensemble des nombres complexes. Il a permis au mathématicien français Henri Poincaré d éclairer les travaux du Russe Nicolaï Lobatchevski. Sommaire 1 Le demi plan de Poincaré (1882) 1.1 Géométrie …   Wikipédia en Français

  • Demi-plan de Poincare — Demi plan de Poincaré Le demi plan de Poincaré est un sous ensemble des nombres complexes. Il a permis au mathématicien français Henri Poincaré d éclairer les travaux du Russe Nicolaï Lobatchevski. Sommaire 1 Le demi plan de Poincaré (1882) 1.1… …   Wikipédia en Français

  • Demi-plan de Poincaré — Le demi plan de Poincaré est un sous ensemble des nombres complexes. Il a permis au mathématicien français Henri Poincaré d éclairer les travaux du Russe Nikolaï Lobatchevski. Sommaire 1 Le demi plan de Poincaré (1882) 1.1 Géométrie 1.1.1 …   Wikipédia en Français

  • Poincare — Poincaré Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Henri Poincaré (1854 1912), mathématicien et philosophe français cousin de Raymond Poincaré. Lucien Poincaré (1862 1920), haut… …   Wikipédia en Français

  • Poincaré — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronyme 2 Mathématiques 3 …   Wikipédia en Français

  • Métrique de Poincaré — En mathématiques, et plus précisément en géométrie différentielle, la métrique de Poincaré, due à Henri Poincaré, est le tenseur métrique décrivant une surface de courbure négative constante. C est la métrique naturelle utilisée pour des calculs… …   Wikipédia en Français

  • Disque De Poincaré — Exemple de droites en représentation conforme …   Wikipédia en Français

  • Disque de Poincare — Disque de Poincaré Exemple de droites en représentation conforme …   Wikipédia en Français

  • Disque de Poincaré — Exemple de droites en représentation conforme …   Wikipédia en Français

  • Disque de poincaré — Exemple de droites en représentation conforme …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”