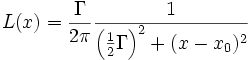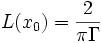Courbe de Lorentz

Courbe de Lorentz

Fonction lorentzienne

On reconnaît une courbe lorentzienne à la forme suivante :

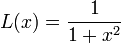
L(x) = \frac{1}{1+x^2}

C'est l'expression la plus simple d'une lorentzienne, centrée en x=0. Une forme paramétrée par l'abscisse x0 du sommet et la largeur Γ à mi-hauteur (couramment appelée largeur de la lorentzienne) est la fonction L définie par :

L(x) = \frac{\Gamma}{2\pi}\frac{1}{\left ( \frac{1}{2}\Gamma\right )^2 + (x-x_0)^2}

En son sommet, elle atteint :

L(x_0) = \frac{2}{\pi \Gamma}

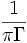C'est la transformée de Fourier d'une exponentielle décroissante de constante de temps \frac{1}{\pi \Gamma}.

C'est une courbe en cloche.

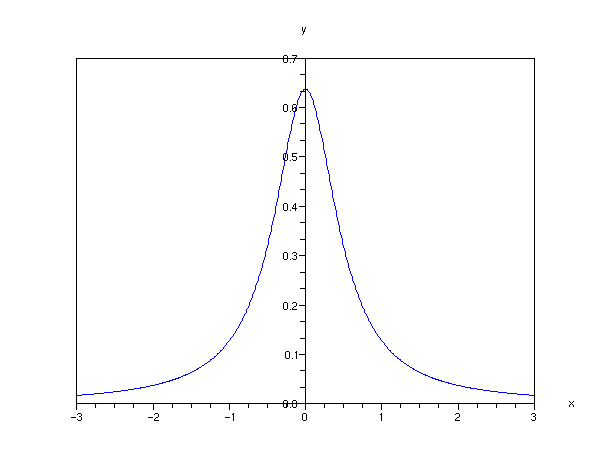
x0 = 0, Γ = 1
Fonction lorentzienne pour x0 = 0, Γ = 1

Sommaire

Applications

En spectrométrie d'émission ou d'absorption, une raie correspond à l'énergie de transition entre deux niveaux électroniques. Le spectre devrait donc présenter une bande de fréquence (ou d'énergie) indéfiniment mince (signal monochromatique). Dans les faits, cette raie a une certaine largeur. Dans le cas d'un gaz, une fonction lorentzienne permet de modéliser la largeur de cette raie (dans un spectre en fréquences) en raison des collisions entre les molécules (élargissement lorentzien) : l'élargissement de la raie est dû à un raccourcissement de la durée d'émission induit par les chocs.

En diffractométrie de rayons X, une fonction lorentzienne permet de décrire le profil des pics de diffraction si l'on considère un effet de taille de cristallites (loi de Scherrer).

Voir aussi

Articles connexes

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction lorentzienne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Courbe de Lorentz de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • SPECTROSCOPIE - Spectroscopie des rayons X — Les principes fondamentaux qui régissent les transitions électroniques du domaine X et qui permettent leur interprétation sont identiques à ceux de la spectroscopie optique. Toutefois, les transitions X présentent des particularités liées au fait …   Encyclopédie Universelle

  • Moindres carrés non linéaires — Les moindres carrés non linéaires est une forme des moindres carrés spécialisée dans l estimation d un modèle non linéaire en n paramètres à partir de m observations (m > n). Une façon d estimer ce genre de problème est de considérer …   Wikipédia en Français

  • Relativité restreinte — Pour les articles homonymes, voir relativité. La relativité restreinte est la théorie formelle élaborée par Albert Einstein en 1905 en vue de tirer toutes les conséquences physiques de la relativité galiléenne et du principe que la vitesse de la… …   Wikipédia en Français

  • Relativite restreinte — Relativité restreinte Pour les articles homonymes, voir relativité …   Wikipédia en Français

  • Effet Sagnac — L effet Sagnac est un phénomène physique découvert par Georges Sagnac en 1913. C est une asymétrie de la vitesse relative de signaux lumineux parcourant en sens inverse la circonférence d un disque en rotation. Sommaire 1 Introduction et… …   Wikipédia en Français

  • ESPACE-TEMPS — La mécanique classique, sous la forme mathématique rigoureuse que lui a donnée Newton, repose sur les deux concepts fondamentaux d’espace et de temps absolus: un événement ponctuel est parfaitement déterminé lorsqu’on connaît sa position dans… …   Encyclopédie Universelle

  • Geometrie de l'espace-temps dans les reperes tournants — Géométrie de l espace temps dans les repères tournants Nous allons aborder dans cet article la géométrie de l espace temps dans un repère en rotation. Plus spécifiquement nous considérerons un disque en rotation et nous allons voir quelle forme… …   Wikipédia en Français

  • Géométrie De L'espace-Temps Dans Les Repères Tournants — Nous allons aborder dans cet article la géométrie de l espace temps dans un repère en rotation. Plus spécifiquement nous considérerons un disque en rotation et nous allons voir quelle forme prend la géométrie de l espace temps pour un observateur …   Wikipédia en Français

  • Géométrie de l'espace-temps dans les repères tournants — Nous allons aborder dans cet article la géométrie de l espace temps dans un repère en rotation. Plus spécifiquement nous considérerons un disque en rotation et nous allons voir quelle forme prend la géométrie de l espace temps pour un observateur …   Wikipédia en Français

  • RELATIVITÉ — En physique, le vocable «relativité» recouvre deux concepts très différents. Celui de relativité restreinte (qui a remplacé la relativité galiléenne ) spécifie la structure cinématique de l’espace temps. Cette structure, d’abord suggérée par… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”