- Courbe de Lorenz
-
Pour l’article homonyme, voir Fonction lorentzienne.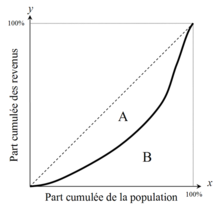 
Courbe de Lorenz. La ligne pointillée représente la ligne d'égalité parfaite. Le coefficient de Gini est définit comme étant deux fois l'aire A.
La courbe de Lorenz a été développée par Max O. Lorenz comme une représentation graphique des inégalités de revenu. Elle peut aussi servir à mesurer les inégalités de répartition d'un actif ou de toute autre distribution de richesse.
La courbe de Lorenz est la représentation graphique de la fonction qui à la part x des ménages les moins riches associe la part y du revenu total qu'ils perçoivent.
La part des ménages, classés par ordre de revenu individuel croissant, est donc en abscisse, et la part du revenu reçu en ordonnée.
Dans une société, on dira que la distribution des revenus est parfaitement égalitaire si tous les ménages reçoivent le même revenu. Alors la part x des ménages les moins riches reçoit une part y=x du revenu global. Une répartition égalitaire est donc représentée par la première bissectrice du repère (d'équation y = x). Cette droite est appelée la ligne d'égalité parfaite.
À l'inverse, on parlera de distribution parfaitement inégalitaire si dans la société considérée, un ménage accapare le revenu total (global). Dans ce cas, la fonction associée prend la valeur y=0 pour tout x<100%, et y=100% quand x=100%. La courbe de Lorenz correspondant à cette situation est appelée la ligne de parfaite inégalité.
La courbe de Lorenz est utilisée pour calculer le coefficient de Gini, qui est égal au double de l'aire de la zone (A) entre la ligne d'égalité parfaite et la courbe de Lorenz : c'est un taux d'inégalité de répartition.
Sommaire
Courbes de Lorenz par pays
France
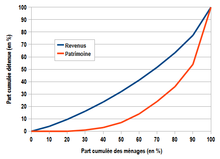Courbe de Lorenz pour les revenus et le patrimoine en France en 2003.Courbe ROC
Dans d'autres domaines (épidémiologie, traitement du signal, psychologie expérimentale), la courbe de Lorenz correspond à ce qu'on appelle la courbe ROC (Receiver Operating Characteristic).
Voir aussi
Articles connexes
Liens externes
- Courbe de Lorenz et coefficient de Giniexplication et démonstration.
- (en) Une fiche technique sur la courbe de Lorenz comprenant divers champs d'application, incluant un fichier Excel traçant la courbe de Lorenz et calculant coefficients de Gini et de variation.
- Courbe ROC
Wikimedia Foundation. 2010.
