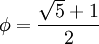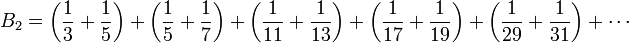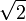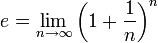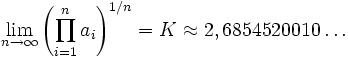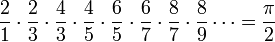Constantes mathematiques (representees en fraction continuee)
- Constantes mathematiques (representees en fraction continuee)
-
Constantes mathématiques (représentées en fraction continuée)
Voici une table de constantes mathématiques exprimées par leurs notations et par leurs représentations en fraction continue :
(Constantes connues comme étant irrationnelles avec un développement en fraction continue infini : leur dernier terme est ....)
 Portail des mathématiques
Portail des mathématiques
Catégorie : Constante mathématique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Constantes mathematiques (representees en fraction continuee) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Constantes Mathématiques (Représentées En Fraction Continuée) — Voici une table de constantes mathématiques exprimées par leurs notations et par leurs représentations en fraction continue : (Constantes connues comme étant irrationnelles avec un développement en fraction continue infini : leur… … Wikipédia en Français
Constantes mathématiques (représentées en fraction continuée) — Voici une table de constantes mathématiques exprimées par leurs notations et par leurs représentations en fraction continue : (Constantes connues comme étant irrationnelles avec un développement en fraction continue infini : leur… … Wikipédia en Français
Table de constantes mathematiques — Table de constantes mathématiques Cet article donne une liste de certaines constantes mathématiques. Typiquement, une constante en mathématique est un élément du corps des nombres réels ou des nombres complexes. À la différence des constantes… … Wikipédia en Français
Table de constantes mathématiques — Cet article donne une liste de certaines constantes mathématiques. Typiquement, une constante en mathématique est un nombre réel ou complexe. À la différence des constantes physiques, les constantes mathématiques sont définies indépendamment de… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Constante mathématique — Table de constantes mathématiques Cet article donne une liste de certaines constantes mathématiques. Typiquement, une constante en mathématique est un élément du corps des nombres réels ou des nombres complexes. À la différence des constantes… … Wikipédia en Français
Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 … Wikipédia en Français
Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 … Wikipédia en Français
Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e … Wikipédia en Français
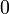

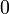
![[0;]\,\!](/pictures/frwiki/57/935b904604aa062eeb36c57356ea2014.png)

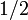
![[0; 2]\,\!](/pictures/frwiki/100/d0a654f93b63022dd93bcb52cc8fe8c9.png)
![C_2= [0; 1, 1, 1, 16, 2, 2, 2, 2, 1, 18, 2, 2, 11, 1, 1, 2, 4, 1, 16, 3, 2, 4, 21, 2, 405, 2, 1, 33, 1,
1] = 0 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/100/de16dd722910e59af11677c9463ced90.png)
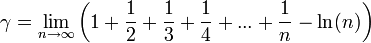 où ln représente le logarithme népérien.
où ln représente le logarithme népérien.![\gamma = [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1,
2, 4, 1, 1, 40, 1, 11, 3, 7, 1, 7, 1, 1, 5, 1, 49, ...] = 0 + \frac{1}{1 + \frac{1}{1 + \frac{2}{1 + \cdots}}}](/pictures/frwiki/98/bc82cec452c072a32b2ed4c5a4d5513e.png)
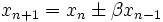 dégénère exponentiellement quand
dégénère exponentiellement quand 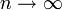 avec une probabilité 1.
avec une probabilité 1.![\beta^{*} = [0; 1, 2, 2, 1, 3, 5, 1, 2, 6, 1, 1, 5] = 0 + \frac{1}{1 + \frac{2}{1 + \frac{2}{1 + \cdots}}}](/pictures/frwiki/56/8ec84afcca5ae1c31ece60642dbaacd2.png)
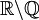 ?
?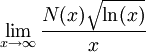 où N(x) est le nombre d'entiers positifs inférieurs à x qui sont la somme de deux carrés.
où N(x) est le nombre d'entiers positifs inférieurs à x qui sont la somme de deux carrés.![K = [0; 1, 3, 4, 6, 1, 15, 1, 2, 2, 3, 1, 23, 3, 1, 1, 3, 1, 1, 7, 2, 3, 3, 18, 2, 1, 2, 1, 2, 1,
6] = 0 + \frac{1}{1 + \frac{3}{1 + \frac{4}{1 + \cdots}}}](/pictures/frwiki/98/bf5e8b51f5f0afdd842400b4b6a161f2.png)
![B_4 = [0; 1, 6, 1, 2, 1, 2, 956, 8, 1, 1, 1, 23] = 0 + \frac{1}{1 + \frac{6}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/49/19fce12d6b2bc314fc351e35714098c0.png)
![K = [0; 1, 10, 1, 8, 1, 88, 4, 1, 1, 7, 22, 1, 2, 3, 26, 1, 11, 1, 10, 1, 9, 3, 1, 1, 1, 1, 1, 1, 2,
2] = 0 + \frac{1}{1 + \frac{10}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/48/0b051c195c56650c29a98958a5142ee5.png)
![M_1= [0; 3, 1, 4, 1, 2, 5, 2, 1, 1, 1, 1, 13, 4, 2, 4, 2, 1, 33, 296, 2, 1, 5, 19, 1, 5, 1, 1, 1, 1,
1] = 0 + \frac{3}{1 + \frac{1}{1 + \frac{4}{1 + \cdots}}}](/pictures/frwiki/102/ff4e62fa2263868c07f6e7ed991a664b.png)
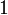

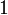
![\phi = [1; 1, 1, 1, ...] = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/53/545cfcd18fedb86cb00f8dd8137ed54d.png)
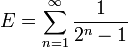
![E_B = [1; 1, 1, 1, 1, 5, 2, 1, 2, 29, 4, 1, 2, 2, 2, 2, 6, 1, 7, 1, 6, 2, 1, 1, 1, 20, 1, 3, 1, 1,
1, ...] = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/54/6948d9347360f7c0c577258ca75213a2.png)
![B_2 = [1; 1, 9, 4, 1, 1, 8, 3, 4, 7, 1, 3, 3, 1, 2, 1, 1, 12, 4, 2, 1, 2, 2] = 1 + \frac{1}{1 + \frac{9}{1 + \frac{4}{1 + \cdots}}}](/pictures/frwiki/48/06304217ffce109b6c86f45e0504b19a.png)
![\sqrt[n]{|f_n|} \to 1,13198824\dots \mbox{quand }n \to \infty.](/pictures/frwiki/54/6e3c091ca34c64c6f20b8fd7c3b4653d.png) où fn est une suite de Fibonacci aléatoire
où fn est une suite de Fibonacci aléatoire![K = [1; 7, 1, 1, 2, 1, 3, 2, 1, 2, 1, 17, 1, 1, 2, 1, 2, 4, 1, 2] = 1 + \frac{7}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/98/b5783926658b7e318222605982760c2c.png)
![\sqrt{2} = [1; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, ...] = 1 + \frac{2}{1 + \frac{2}{1 + \frac{2}{1 + \cdots}}}](/pictures/frwiki/97/aa76f5b91e4131081ec67ca269da7407.png)
![\mu = [1; 2, 4, 1, 1, 1, 3, 1, 1, 1, 2, 47, 2, 4, 1, 12, 1, 1, 2, 2, 1, 7, 2, 1, 1, 1, 2, 30, 6, 3,
6] = 1 + \frac{2}{1 + \frac{4}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/53/52f392f552a06c296150a38186d5c2ec.png)
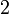

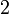
![[2;]\,\!](/pictures/frwiki/53/53beffacdfe66522dcd5dde82938178d.png)
![\alpha = [2; 1, 1, 85, 2, 8, 1, 10, 16, 3, 8, 9, 2, 1, 40, 1, 2, 3, 2, 2, 1, 17, 1, 1, 5, 3, 2, 6, 3, 5, 1] = 2 + \frac{1}{1 + \frac{1}{1 + \frac{85}{1 + \cdots}}}](/pictures/frwiki/53/5ec873fc3ccf4b20bab5be2fbd4bea14.png)
![e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, 1, 16, 1, 1, 18, 1, 1, 20, 1, ...] = 2 + \frac{1}{1 + \frac{2}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/99/c75b68077979560737422168cf24193d.png)
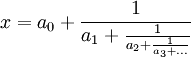 , il est presque toujours vrai que
, il est presque toujours vrai que![K_h = [2; 1, 2, 5, 1, 1, 2, 1, 1, 3, 10, 2, 1, 3, 2, 24, 1, 3, 2, 3, 1, 1, 1, 90] = 2 + \frac{1}{1 + \frac{2}{1 + \frac{5}{1 + \cdots}}}](/pictures/frwiki/53/504b7bcc9a93327488354fbbe1e08261.png)

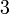
![[3;]\,\!](/pictures/frwiki/56/8374d111f8e965b5c02bf508d79c887a.png)
![\pi = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15, 3, 13, 1,
4, 2, ...] = 3 + \frac{7}{1 + \frac{15}{1 + \frac{1}{1 + \cdots}}}](/pictures/frwiki/101/e6a97d7b209126c8c8fe13eb1846b658.png)

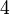
![[4;]\,\!](/pictures/frwiki/50/2bf4485a6d4c8c4d62572aae7f585284.png)
![\delta = [4; 1, 2, 43, 2, 163, 2, 3, 1, 1, 2, 5, 1, 2, 3, 80, 2, 5, 2, 1, 1, 1, 33, 1, 1, 53, 1, 1, 1, 1, 1] = 4 + \frac{1}{1 + \frac{2}{1 + \frac{43}{1 + \cdots}}}](/pictures/frwiki/99/cf9e8d4aef5d6fc07ab3dd2160b8c0a6.png)

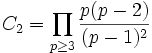
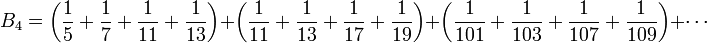
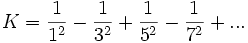
![M = \lim_{n \rightarrow \infty } \left(
\sum_{p \leq n} \frac{1}{p} - \ln(\ln(n)) \right)=\gamma + \sum_{p} \left[ \ln \left( 1 - \frac{1}{p} \right) + \frac{1}{p} \right]](/pictures/frwiki/53/5e64515f3b653026f658bf6cdc98834a.png)