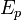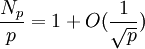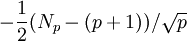Conjecture de satō-tate

En mathématiques, la conjecture de Satō-Tate est un énoncé statistique à propos de la famille des courbes elliptiques

sur le corps fini à p éléments, avec p un nombre premier, obtenu à partir d'une courbe elliptique E sur le corps des nombres rationnels, par le processus de réduction modulo un nombre premier pour presque tous les p. Si

désigne le nombre de points sur E_p et défini sur le corps à p éléments, la conjecture donne une réponse à la distribution du terme du deuxième ordre pour 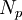. C’est-à-dire, par le théorème de Hasse, nous avons

lorsque 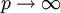, l'objectif de la conjecture étant de prédire comment le terme O varie.

Sommaire 1 Détails 2 L'annonce de Taylor 3 Généralisation 4 Questions plus précises 5 Lien externe

Détails

Il est facile de voir que nous pouvons, en fait, choisir le premier M des E_p comme nous voulons, comme une application du théorème des restes chinois, pour un entier M quelconque fixé. Dans le cas où E possède une multiplication complexe la conjecture est remplacée par une autre loi, plus simple.

Il est connu, à partir de la théorie générale que le reste

peut être exprimé sous la forme 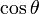pour un angle 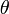; en termes géométriques, il existe deux valeurs propres comptant pour le reste et avec le dénominateur donné, il existe des conjugués complexes et de valeur absolue 1. La conjecture de Satō-Tate, lorsque E n'a pas de multiplication complexe, établit la mesure de probabilité de 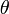est proportionnelle à

.

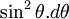Ceci est dû à Mikio Satō et John Tate (indépendamment, et aux environs de 1960 édité quelque temps plus tard).

L'annonce de Taylor

Le 18 mars 2006, Richard Taylor de l'Université d'Harvard a annoncé sur sa page web une démonstration de la conjecture de Satō-Tate pour les courbes elliptiques sur les corps totalement réels satisfaisant une certaine condition : d'avoir une réduction multiplicative à un certain nombre premier. C’est-à-dire, pour un certain p où E a une mauvaise réduction (et au moins pour les courbes elliptiques sur les nombres rationnels, il y a quelques p de cette sorte), le type dans la fibre singulière du modèle de Néron est multiplicatif, plutôt qu'additif. En pratique, ceci est un cas typique, donc la condition peut être pensée comme douce.

Généralisation

Il existe des généralisations, impliquant la distribution des éléments de Frobenius dans les groupes de Galois impliqués dans les représentations de Galois sur la cohomologie étale. En particulier, il existe une théorie conjecturale pour les courbes de genre > 1.

La forme de la distribution conjecturée est quelque chose qui peut être lue à partir de la géométrie des groupes de Lie d'un cas donné; de sorte qu'en termes généraux, il existe un raisonnement pour cette distribution particulière. En fait, cette distribution se décrit de manière naturelle: c'est la mesure image, sur l'espace des classes de conjugaison, de la mesure de Haar du groupe de Lie compact considéré. On trouve le cas classique pour SU(2), quitte à paramétrer les classes de conjugaisons par leur valeur deux valeurs propres conjuguées, voire leur argument θ.

Questions plus précises

Il existes des énoncés plus raffinés. La conjecture de Lang-Trotter (1976) de Serge Lang et Hale Trotter prédit le nombre asymptotique de nombre premiers p avec une valeur donnée de 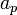, la trace de Frobenius qui apparaît dans la formule. Pour le cas typique (pas de multiplication complexe, trace ≠ 0) leur formule établit que le nombre de p jusqu'à X est asymptotiquement

avec une constante C précise. Neal Koblitz (1988) a fourni des conjectures détaillées pour le cas d'un nombre premier q de points sur E_p, motivé par la cryptographie sur les courbes elliptiques.

Lien externe

• Diagrammes illustrant la conjecture de Satō-Tate, faits avec le logiciel d'algèbre SAGE.

• Portail des mathématiques