- Module de Galois
-
Représentation galoisienne
La théorie des représentations galoisiennes est l'application naturelle de la théorie des représentations à la théorie algébrique des nombres. Un module galoisien est un module sur lequel agit un groupe de Galois G. Ces modules seront par exemple des groupe d'unité, des groupes des classes, ou des groupes de Galois eux-mêmes.
Base normale d'entiers
En théorie algébrique des nombres classique, soit L une extension de corps K, et soit G le groupe de Galois correspondant. Alors l'anneau OL d'entiers de L peut être considéré comme un OK[G]-module. Le théorème de la base normale assure que L est un K[G]-module libre de rang 1 ; c'est un résultat de théorie des corps. La question arithmétique analogue peut donc s'énoncer : OL est-il un OK[G]-module de rang 1. C'est la question de l'existence d'une base normale d'entiers, c'est-à-dire d'
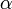 dans OK tel que ses éléments conjugués sous G donnent une OK-base de OL. Cette question se pose particulièrement dans le cas où K est le corps
dans OK tel que ses éléments conjugués sous G donnent une OK-base de OL. Cette question se pose particulièrement dans le cas où K est le corps 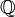 des nombres rationnels.
des nombres rationnels.En fait, tous les sous-corps des corps cyclotomiques, c'est-à-dire des Q(ζp) où ζp est une racine p-ième de l'unité pour p un nombre premier, ont des bases normales d'entiers (sur
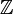 ) ; ceci se déduit de la théorie des périodes de Gauss. En revanche, le corps de Gauss Q(i) n'en admet pas. En fait, ces exemples s'insrivent dans le cadre plus général d'une condition nécessaire trouvée par la mathématicienne Emmy Noether : en prenant
) ; ceci se déduit de la théorie des périodes de Gauss. En revanche, le corps de Gauss Q(i) n'en admet pas. En fait, ces exemples s'insrivent dans le cadre plus général d'une condition nécessaire trouvée par la mathématicienne Emmy Noether : en prenant 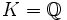 le théorème de Noether établit que le fait que la ramification soit modérée est nécessaire et suffisante pour que OL soit un module projectif sur Z[G]. C'est par conséquent une condition nécessaire pour qu'il soit un module libre. Cela laisse en suspens la question de la différence entre libre et projectif, pour lequel beaucoup de travail a maintenant été fait.
le théorème de Noether établit que le fait que la ramification soit modérée est nécessaire et suffisante pour que OL soit un module projectif sur Z[G]. C'est par conséquent une condition nécessaire pour qu'il soit un module libre. Cela laisse en suspens la question de la différence entre libre et projectif, pour lequel beaucoup de travail a maintenant été fait.Cohomologie étale
Dans le cas d'un groupe G profini, c'est-à-dire si G est groupe de Galois d'une extension infinie, il existe une grande quantité de G-modules disponibles en théorie cohomologie étale, qui est une théorie algébrique (et par conséquent exhibe la 'covariance' en ce qui concerne la symétrie de Galois). Une découverte de base des années 1960 montre que de tels modules sont comme non-triviaux comme ils peuvent être, en général; de sorte que la théorie des plutôt riche.
Programme de Langlands
Catégorie : Théorie algébrique des nombres
Wikimedia Foundation. 2010.
