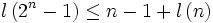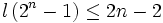Conjecture de scholz

Conjecture de Scholz

En mathématiques, la conjecture de Scholz, parfois appelée conjecture de Scholz-Brauer ou conjecture de Brauer-Scholz, fut proposée en 1937. Elle prétend que

$l \left( 2^n - 1 \right) \le n - 1 + l \left( n \right)$

où l(n) est la plus courte chaîne d'additions qui vaut n. Elle a été démontrée dans de nombreux cas, mais pas dans le cas général.

Par exemple, l(5)=3 (puisque 1+1=2, 2+2=4, 4+1=5 et il n'existe pas de chaîne plus courte) et l(31)=7 (1+1=2, 2+1=3, 3+3=6, 6+6=12, 12+12=24, 24+6=30, 30+1=31), alors

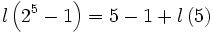$l \left( 2^5 - 1 \right) = 5 - 1 + l \left( 5 \right)$ .

Des recherches en théorie des nombres et sur la nature des chaînes d'additions ont permis d'établir cette égalité, plus faible :

$l \left( 2^n - 1 \right) \le 2 n - 2$

Une preuve qui permet de passer des n à l(n) n'a pas encore été trouvée.

Liens externes

(en) Plus courte chaîne d'additions
(en) OEIS séquence A003313

Références

Scholz, A., "Jahresbericht" Deutsche Math. Vereingung 1937 pp. 41-42
Brauer, A. T., "On addition chains" Bull. Amer. Math. Soc. 1939 pp. 637-739

Portail des mathématiques

Ce document provient de « Conjecture de Scholz ».

Catégories : Conjecture | Analyse

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture de scholz de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Conjecture De Scholz — En mathématiques, la conjecture de Scholz, parfois appelée conjecture de Scholz Brauer ou conjecture de Brauer Scholz, fut proposée en 1937. Elle prétend que où l(n) est la plus courte chaîne d additions qui vaut n. Elle a été démontrée dans de… … Wikipédia en Français
Conjecture de Scholz — En mathématiques, la conjecture de Scholz, parfois appelée conjecture de Scholz Brauer ou conjecture de Brauer Scholz, fut proposée en 1937. Elle prétend que où l(n) est la longueur de la plus courte chaîne d additions (en) qui produit n, c… … Wikipédia en Français
Scholz — is a German surname.* Rupert Scholz (born 1937), German politician * Heiko Scholz(born 1966) * Donald Thomas Scholz (born 1947), guitarist * Jackson Scholz (1897 1986), American athlete * Franz Scholz (1909 1998) priest and professor of theology… … Wikipedia
Scholz conjecture — In mathematics, the Scholz conjecture (sometimes called the Scholz Brauer conjecture or the Brauer Scholz conjecture) is a conjecture from 1937 stating that: l (2 n −1) le; n − 1 + l ( n )where l ( n ) is the length of the shortest addition chain … Wikipedia
Proof of weak Scholz conjecture — In mathematics, a weaker version of the Scholz conjecture about addition chains can be proven without advanced number theory. In fact, proving the inequality: l (2 n − 1) le; 2n − 2is simple, providing some basic observations are made.First of… … Wikipedia
Liste Des Conjectures Mathématiques — Ce qui suit est une liste de conjectures mathématiques, contenues dans les pages de Wikipedia. Elles sont divisées en quatre sections, en accord avec leur état en 2006. Voir aussi : La conjecture d Erdős, qui liste les conjectures de Paul… … Wikipédia en Français
Liste des conjectures — mathématiques Ce qui suit est une liste de conjectures mathématiques, contenues dans les pages de Wikipedia. Elles sont divisées en quatre sections, en accord avec leur état en 2006. Voir aussi : La conjecture d Erdős, qui liste les… … Wikipédia en Français
Liste des conjectures mathematiques — Liste des conjectures mathématiques Ce qui suit est une liste de conjectures mathématiques, contenues dans les pages de Wikipedia. Elles sont divisées en quatre sections, en accord avec leur état en 2006. Voir aussi : La conjecture d Erdős,… … Wikipédia en Français
Liste des conjectures mathématiques — Ce qui suit est une liste de conjectures mathématiques, contenues dans les pages de Wikipedia. Elles sont divisées en quatre sections, en accord avec leur état en 2006. Voir aussi : La conjecture d Erdős, qui liste les conjectures de Paul… … Wikipédia en Français
Liste de conjectures mathématiques — Ce qui suit est une liste de conjectures mathématiques, non exhaustive. Elles sont divisées en quatre sections, en accord avec leur état en 2011. Voir aussi : Conjecture d Erdős (en), qui liste des conjectures de Paul Erdős et de ses… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Conjecture de scholz