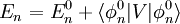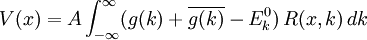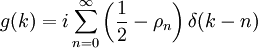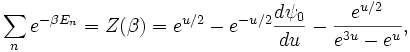Conjecture de Hilbert-Polya

En mathématiques, la conjecture de Hilbert-Pólya est une approche possible de l'hypothèse de Riemann, à l'aide de la théorie spectrale.

Sommaire 1 Premières idées 2 Les années 50 et la formules des traces de Selberg 3 Les années 70 et les matrices aléatoires 4 Développements récents 5 Connexion possible avec la mécanique quantique 6 Connexion possible avec la mécanique statistique

Premières idées

Hilbert et Pólya ont spéculé que les valeurs de t telle que 1/2 + it soit un zéro de la fonction zêta de Riemann doivent être les valeurs propres d'un opérateur hermitien, et ceci serait une voie pour démontrer l'hypothèse de Riemann.

Les années 50 et la formules des traces de Selberg

À ce moment, c'était une petite base pour une telle spéculation. Néanmoins Selberg au début des années 1950 a démontré une dualité entre la longueur du spectre d'une surface de Riemann et les valeurs propres de son laplacien. Ceci, que l'on appelle la formule des traces de Selberg avance une ressemblance frappante avec les formules explicites, donna une certaine crédibilité à la spéculation de Hilbert et Pólya.

Les années 70 et les matrices aléatoires

Hugh Montgomery rechercha et trouva que la distribution statistique des zéros sur la droite critique possède une certaine propriété. Les zéros ne tendent pas à être trop fermement ensemble, mais à se repousser. En visitant l'Institute for Advanced Study en 1972, il montra ce résultat à Freeman Dyson, un des fondateurs de la théorie des matrices aléatoires, qui sont très importantes en physique — les états propres d'un hamiltonien, par exemple les niveaux d'énergie d'un noyau atomique, satisfont à de telles statistiques.

Dyson a vu que la distribution statistique trouvée par Montgomery était exactement la même que la distribution des paires de corrélations pour les valeurs propres d'une matrice hermitienne aléatoire. Le travail postérieur a fortement élevé cette découverte, et la distribution des zéros de la fonction zêta de Riemann est maintenant reconnue pour satisfaire les mêmes statistiques que les valeurs propres d'une matrice hermitienne aléatoire, les statistiques de ce que l'on appelle l'ensemble unitaire gaussien. Ainsi, la conjecture de Pólya et Hilbert possède maintenant une base plus solide, bien qu'elle n'ait pas encore conduit à une démonstration de l'hypothèse de Riemann.

Développements récents

Dans un développement qui a donné une force appréciable à cette approche de l'hypothèse de Riemann à travers l'analyse fonctionnelle, Alain Connes a énoncé une formule de trace qui est actuellement équivalente à l'hypothèse de Riemann généralisée. Ceci a, par conséquent, renforcé l'analogie avec la formule de trace de Selberg au point où elle donne des résultats précis.

Connexion possible avec la mécanique quantique

Une connexion possible de l'opérateur de Hilbert-Pólya avec la mécanique quantique a été donnée par Pólya. L'opérateur de Hilbert-Pólya est de la forme 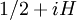où 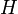est l'Hamiltonien d'une particule de masse 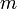c’est-à-dire se déplaçant sous l'influence d'un potentiel V(x). La conjecture de Riemann est équivalente à l'affirmation que l'Hamiltonien est Hermitien, ou de manière équivalente que V est réel.

En utilisant la théorie de la perturbation du premier ordre, l'énergie du nième état propre est relié à la valeur espérée du potentiel :

où 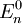et 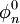sont les valeurs propres et les états propres de l'Hamiltonien de la particule libre. Cette équation peut être prise pour être une équation intégrale de Fredholm de première espèce, avec les énergies E_n. De telles équations intégrales peuvent être résolues au moyen du noyau résolvant, de sorte que le potentiel peut être écrit sous la forme

où R(x,k) est le noyau résolvant, A est une constante réelle et

où 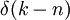est la fonction delta de Dirac, et les 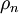sont les racines "non-triviales" de la fonction zêta .

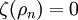Connexion possible avec la mécanique statistique

En utilisant la formule explicite pour la fonction de Tchebychef, en fixant x=exp(u), nous avons

où Z est une fonction de partition, par conséquent est la trace de l'exponentielle d'un certain Hamiltonien où "bêta" est une quantité imaginaire pure.

En utilisant la définition de Z en termes d'une intégrale sur (x, p), nous avons l'intégrale non-linéaire prochaine pour le potentiel :

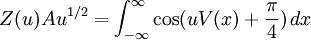with − β = iu.

Donc, l'opétateur de Hilbert-Pólya est un Hamiltonien, dont les "énergies" sont précisément les parties imaginaires des nombres satisfaisant .

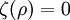• Portail des mathématiques
• Portail de la physique