Coefficient de Gini

Coefficient de Gini
Page d'aide sur l'homonymie Pour les articles homonymes, voir Gini (homonymie).

Le coefficient de Gini est une mesure du degré d'inégalité de la distribution des revenus dans une société donnée, développée par le statisticien italien Corrado Gini.

Le coefficient de Gini est un nombre variant de 0 à 1, où 0 signifie l'égalité parfaite (tout le monde a le même revenu) et 1 signifie l'inégalité totale (une personne a tout le revenu, les autres n'ont rien, cas extrême du maître et de ses esclaves).

Sommaire

Calcul du coefficient de Gini

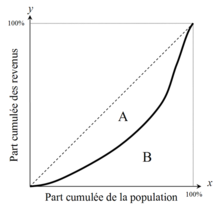Courbe de Lorenz et coefficient de Gini (2 fois A)

Le coefficient de Gini se calcule par rapport à la fonction (dont la représentation graphique est la courbe de Lorenz) qui associe à chaque part de la population ordonnée par revenu croissant, la part que représente ses revenus.

Il estime l'inégalité par l'écart à la courbe de Lorenz de la répartition égale (en pointillés) : c'est le double de la surface (A) qui sépare la courbe de Lorenz de la situation étudiée (en gras) de la droite d'égalité.

G = 2A = 2(A+B-B) = 2(A+B) - 2B = 1 - 2B

(A+B est le triangle moitié du carré 1x1)

Le coefficient de Gini est égal à la différence entre 1 et le double de l'intégrale de la fonction représentée par la courbe de Lorenz.

En pratique, on ne dispose pas de cette fonction, mais du revenu par « tranches » de la population. Pour n tranches, le coefficient s'obtient par la formule de Brown :

G = 1 - \sum_{k=0}^{k=n-1} (X_{k+1} - X_{k}) (Y_{k+1} + Y_{k})

où X est la part cumulée de la population, et Y la part cumulée du revenu.


Pour n personnes ayant des revenus yi, pour i allant de 1 à n, indicés par ordre croissant ( yi ≤ yi+1):

G = \frac{2 \Sigma_{i=1}^n \; i y_i}{n \Sigma_{i=1}^n y_i} -\frac{n+1}{n}

Quelques exemples

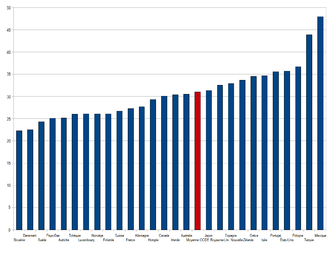
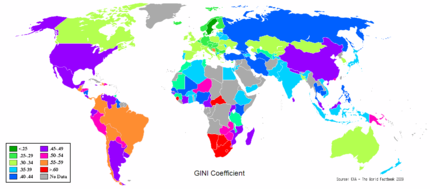
Article détaillé : Liste des pays par égalité de revenus.
Coefficient de Gini pour la distribution du revenu disponible des ménages en 2000 dans les pays de l'OCDE.
Coefficient de Gini en 2009

Les pays les plus égalitaires ont un coefficient de l'ordre de 0,2 (Danemark, Suède, Japon, République tchèque...). Les pays les plus inégalitaires au monde ont un coefficient de 0,6 (Brésil, Guatemala, Honduras, ...). En France, le coefficient de Gini est de 0,289[1]. Celui de la Chine est en train d'augmenter et avoisine désormais 0,5.

Autres applications

Le coefficient de Gini est principalement utilisé pour mesurer l'inégalité de revenu, mais peut aussi servir à mesurer l'inégalité de richesse ou de patrimoine. Le coefficient de Gini en économie est souvent combiné avec d'autres données. Se situant dans le cadre de l'étude des inégalités, il va de pair avec la politique. Ses liens avec l'indicateur démocratique (élaboré par des chercheurs, entre -2.5 au pire et +2.5 au mieux) sont réels mais pas automatiques.[réf. nécessaire]

Il est aussi utilisé par les logisticiens en entrepôts pour étudier l'implantation des références en fonction des statistiques de sorties des articles. En informatique, le coefficient de Gini est employé dans le cadre de certaines méthodes d'apprentissage supervisé, comme les arbres de décision.

Amartya Sen a proposé une « fonction du bien-être » : PIB (1 - coefficient de Gini) comme alternative à la médiane[2].

  • explication et démonstration, voir le lien :

http://www.4shared.com/document/ZYtYBV5V/Courbe_de_Lorenz_et_coefficien.html

Références

  1. ↑ http://www.insee.fr/fr/themes/document.asp?ref_id=erfs2007
  2. ↑ James E. Foster und Amartya Sen: On Economic Inequality, expanded edition with annexe, 1996, ISBN 0-19-828193-5

Voir aussi

Lien interne

Liens externes

Littérature

  • Y. Amiel: Thinking about inequality, Cambridge 1999.
  • C. Gini: Measurement of inequality of income, in: Economic Journal 31 (1921), 22-43.
  • Amartya Sen: On Economic Inequality (Enlarged Edition with a substantial annexe “On Economic Inequality” after a Quarter Century with James Foster), Oxford 1997, ISBN 0-19-828193-5

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Coefficient de Gini de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Coefficient De Gini — Pour les articles homonymes, voir Gini (homonymie). Courbe de Lorenz et coefficient de Gini Le coefficient de Gini est une mesure du degré d inégalité …   Wikipédia en Français

  • Coefficient de GINI — Pour les articles homonymes, voir Gini (homonymie). Courbe de Lorenz et coefficient de Gini Le coefficient de Gini est une mesure du degré d inégalité …   Wikipédia en Français

  • Coefficient de gini — Pour les articles homonymes, voir Gini (homonymie). Courbe de Lorenz et coefficient de Gini Le coefficient de Gini est une mesure du degré d inégalité …   Wikipédia en Français

  • Gini — (homonymie) Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Gini peut être : une boisson : Gini une mesure d inégalité des revenus : Coefficient de Gini un statisticien et sociologue… …   Wikipédia en Français

  • Gini (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Gini peut être : une boisson : Gini une mesure d inégalité des revenus : Coefficient de Gini un statisticien et sociologue italien :… …   Wikipédia en Français

  • Gini — can have several meanings:*G.I.N.I., a predecessor organization to Post Polio Health International *Corrado Gini, an Italian statistician, demographer, sociologist and developer of the Gini coefficient, which measures income inequality in a… …   Wikipedia

  • GINI (INDICE DE) — Dès que l’on s’interroge sur le point de savoir si les inégalités (de revenu, de niveau scolaire, et autres) sont plus ou moins grandes dans telle société que dans telle autre, ou si elles ont tendance à croître ou à diminuer dans une société… …   Encyclopédie Universelle

  • Gini coefficient — coefficient developed by Corrado Gini which is a number between zero and one that is a measure of inequality …   English contemporary dictionary

  • coefficient — UK US /ˌkəʊɪˈfɪʃənt/ noun [C] ► in mathematics, a value that appears in front of and multiplies another value: »In 2x + 4y = 7, 2 is the coefficient of x. ► a number or a method of calculating a number that measures the characteristics of a… …   Financial and business terms

  • Gini coefficient — The Gini coefficient is a measure of statistical dispersion most prominently used as a measure of inequality of income distribution or inequality of wealth distribution. It is defined as a ratio with values between 0 and 1: A low Gini coefficient …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”