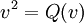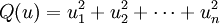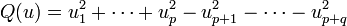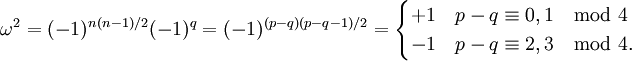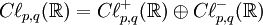Classification Des Algèbres De Clifford

Classification des algèbres de Clifford

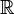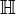En mathématiques, en particulier dans la théorie des formes quadratiques non dégénérées sur les espaces vectoriels réels et complexes, les algèbres de Clifford de dimension finie ont été complètement classées. Dans chaque cas, l'algèbre de Clifford est isomorphe à une algèbre de matrices sur $\mathbb{R}\,$ , $\mathbb{C}\,$ , ou $\mathbb{H}\,$ (les quaternions), ou à une somme directe de deux de ces algèbres, bien que ce ne soit pas la manière canonique.

Notation et conventions. Dans cet article, nous utiliserons la convention de signe (+) pour la multiplication de Clifford, c’est-à-dire

$v^2 = Q(v)\,$

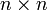pour tous les vecteurs $v \in V\,$ , où Q est la forme quadratique sur l'espace vectoriel V. Nous désignerons l'algèbre de matrices $n \times n\,$ avec les entrées dans l'algèbre de division K par K(n). La somme directe des algèbres sera désignée par K²(n) = K(n) ⊕ K(n).

Le cas complexe

Le cas complexe est particulièrement simple : chaque forme quadratique non dégénérée forme sur un espace vectoriel complexe est équivalente à la forme diagonale standard

$Q(u) = u_1^2 + u_2^2 + \cdots + u_n^2$

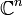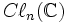où n = dim V, donc, il existe essentiellement une seule algèbre de Clifford dans chaque dimension. Nous noterons l'algèbre de Clifford sur $\mathbb{C}^n\,$ avec la forme quadratique standard par $C\ell_{n}(\mathbb{C})\,$ .

Il existe deux cas séparés à considérer, suivant que n est pair ou impair. Lorsque n est pair, l'algèbre 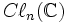$C\ell_{n}(\mathbb{C})\,$ est centrale simple et donc, par le théorème d'Artin-Wedderburn est isomorphe à l'algèbre de matrice sur $\mathbb{C}\,$ . Lorsque n est impair, le centre inclus non seulement les scalaires mais aussi les pseudoscalaires (éléments de degré n). Nous pouvons toujours trouver un pseudoscalaire normalisé $\omega\,$ tel que $\omega^2 = 1\,$ . Définissons les opérateurs

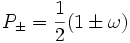$P_{\pm} = \frac{1}{2}(1\pm\omega)$ .

Ces deux opérateurs forment un ensemble complet d'éléments idempotents orthogonal, et puisqu'ils sont centraux, ils donnent une décomposition de 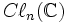$C\ell_{n}(\mathbb{C})\,$ en une somme directe de deux algèbres

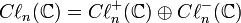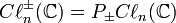$C\ell_n(\mathbb{C}) = C\ell_n^{+}(\mathbb{C}) \oplus C\ell_n^{-}(\mathbb{C})$ où $C\ell_n^\pm(\mathbb{C}) = P_\pm C\ell_n(\mathbb{C})$ .

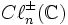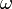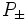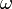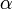Les algèbres $C\ell_{n}^{\pm}(\mathbb{C})\,$ sont simplement les espaces propres positifs et négatifs d' $\omega\,$ et les $P_{\pm}\,$ sont simplement les opérateurs de projection. Puisque $\omega\,$ est impair, ces algèbres sont mélangées par $\alpha\,$ :

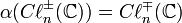$\alpha(C\ell_n^\pm(\mathbb{C})) = C\ell_n^\mp(\mathbb{C})$ .

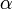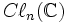et par conséquent isomorphes (puisque $\alpha\,$ est un automorphisme). Ces deux algèbres isomorphes sont chacune simple centrale et donc, de nouveau, isomorphes à une algèbre de matrices sur $\mathbb{C}\,$ . Les tailles de ces matrices peuvent être déterminées à partir du fait que la dimension de $C\ell_{n}(\mathbb{C})\,$ est $2^n\,$ . Ce que nous obtenons alors, c'est la table suivante :

n	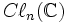$C\ell_{n}(\mathbb{C})\,$
2m	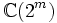$\mathbb{C}(2^m)\,$
2m+1	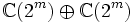$\mathbb{C}(2^m) \oplus \mathbb{C}(2^m)\,$

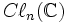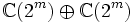La sous-algèbre paire de $C\ell_{n}(\mathbb{C})\,$ est (non-canoniquement) isomorphe à $C\ell_{n-1}(\mathbb{C})\,$ . Lorsque n est pair, les sous-algèbres paires peuvent être identifiées avec les matrices diagonales en blocs (lorsqu'elles sont séparées en matrice en bloc 2 ×2). Lorsque n est impair, les sous-algèbres paires sont ces éléments de $\mathbb{C}(2^m) \oplus \mathbb{C}(2^m)\,$ pour lesquels les deux facteurs sont identiques. 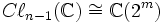En rassemblant l'une et l'autre pièce, cela donne un isomorphisme avec $C\ell_{n-1}(\mathbb{C}) \cong \mathbb{C}(2^m)$ .

Le cas réel

Le cas réel est légèrement plus compliqué, exhibant une périodicité 8 plutôt que 2. Chaque forme quadratique non dégénérée sur un espace vectoriel réel est équivalent à la forme diagonale standard :

$Q(u) = u_1^2 + \cdots + u_p^2 - u_{p+1}^2 - \cdots - u_{p+q}^2$

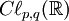où n = p + q est la dimension de l'espace vectoriel. La paire d'entiers (p, q) est appelée la signature de la forme quadratique. L'espace vectoriel réel avec cette forme quadratique est souvent noté $\mathbb{R}^{p,q}\,$ . L'algèbre de Clifford sur $\mathbb{R}^{p,q}\,$ est notée $C\ell_{p,q}(\mathbb{R})\,$ .

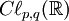Une base orthonormale standard {e_i} pour $\mathbb{R}^{p,q}\,$ consiste en n = p + q vecteurs mutuellement orthogonaux, p est de norme +1 et q est de norme -1. L'algèbre $C\ell_{p,q}(\mathbb{R})\,$ aura par conséquent p vecteurs dont le carré sera +1 et q vecteurs dont le carré sera -1. L'unité pseudoscalaire dans 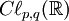$C\ell_{p,q}(\mathbb{R})\,$ est définie par

$\omega = e_1e_2\cdots e_{n}.$

Le carré d' 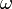$\omega\,$ est donné par

$\omega^2 = (-1)^{n(n-1)/2}(-1)^q = (-1)^{(p-q)(p-q-1)/2} = \begin{cases}+1 & p-q \equiv 0,1 \mod{4}\\ -1 & p-q \equiv 2,3 \mod{4}.\end{cases}$

À noter, à la différence du cas complexe, qu'il n'est pas toujours possible de trouver un pseudoscalaire dont le carré est +1.

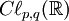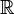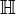La classification s'ensuit : si n est paire (de manière équivalente, si p - q est pair) l'algèbre $C\ell_{p,q}(\mathbb{R})\,$ est simple centrale et donc est isomorphe à une algèbre de matrices sur $\mathbb{R}\,$ ou $\mathbb{H}\,$ par le théorème d'Artin-Wedderburn. Si n (ou p - q) est impair, alors l'algèbre n'est pas simple centrale mais possède plutôt un centre qui inclut les pseudoscalaires aussi bien que les scalaire. Si n est impair et 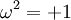$\omega^2 = +1\,$ alors, comme dans le cas complexe, l'algèbre 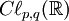$C\ell_{p,q}(\mathbb{R})\,$ se décompose en une somme directe d'algèbres isomorphes

$C\ell_{p,q}(\mathbb{R}) = C\ell_{p,q}^{+}(\mathbb{R})\oplus C\ell_{p,q}^{-}(\mathbb{R})$

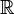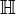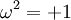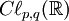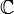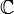chacune est simple centrale et donc isomorphe à l'algèbre de matrice sur $\mathbb{R}\,$ ou $\mathbb{H}\,$ . Si n est impair et $\omega^2 = +1\,$ alors le centre de $C\ell_{p,q}(\mathbb{R})\,$ est isomorphe à $\mathbb{C}$ et peut être considérée comme une algèbre complexe. Comme une algèbre complexe, elle est simple centrale et donc, isomorphe à une algèbre de matrice sur $\mathbb{C}$ .

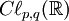Tout indique qu'il existe trois propriétés qui déterminent la classe de l'algèbre $C\ell_{p,q}(\mathbb{R})\,$ :

n est pair/impair,
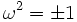$\omega^2 = \pm 1\,$ ,
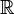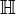La classe de Brauer de l'algèbre (n pair) ou de la sous-algèbre paire (n impair) est $\mathbb{R}\,$ ou $\mathbb{H}\,$ .

Chacune de ces propriétés dépend seulement de la signature p - q modulo 8. La table de classification complète est donnée ci-dessous. La taille des matrices est déterminée par la condition que 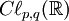$C\ell_{p,q}(\mathbb{R})\,$ ont une dimension $2^{p+q}\,$ .

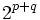p - q mod 8	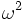$\omega^2\,$	$\mathbb{R}^{p,q}\,$ (p+q = 2m)	p - q mod 8	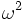$\omega^2\,$	$\mathbb{R}^{p,q}\,$ (p+q = 2m + 1)
0	+	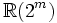$\mathbb{R}(2^m)\,$	1	+	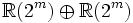$\mathbb{R}(2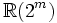^m) \oplus \mathbb{R}(2^m)\,$
2	-	$\mathbb{R}(2^m)\,$	3	-	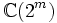$\mathbb{C}(2^m)\,$
4	+	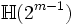$\mathbb{H}(2^{m-1})\,$	5	+	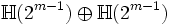$\mathbb{H}(2^{m-1})\oplus\mathbb{H}(2^{m-1})\,$
6	−	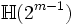$\mathbb{H}(2^{m-1})\,$	7	−	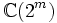$\mathbb{C}(2^m)\,$

Ce qui suit est une table de cette classification pour p + q \le 8. Ici p + q est placé verticalement et p - q horizontalement (par ex. l'algèbre 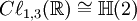$C\ell_{1,3}(\mathbb{R}) \cong \mathbb{H}(2)\,$ est trouvée ligne 4, colonne - 2).

- 1

- 2

- 3

- 4

- 5

- 6

- 7

- 8

$\mathbb{R}\,$

$\mathbb{R}^2\,$

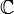
$\mathbb{C}$

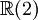
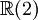
$\mathbb{R}(2)\,$

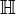
$\mathbb{H}\,$

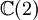
$\mathbb{C}(2)\,$

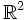
$\mathbb{R}^2\,$

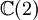
$\mathbb{C}(2)\,$

$\mathbb{H}^2\,$

$\mathbb{H}(2)\,$

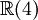
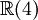
$\mathbb{R}(4)\,$

$\mathbb{H}(2)\,$

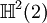
$\mathbb{H}^2(2)\,$

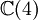
$\mathbb{C}(4)\,$

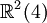
$\mathbb{R}^2(4)\,$

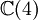
$\mathbb{C}(4)\,$

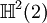
$\mathbb{H}^2(2)\,$

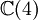
$\mathbb{C}(4)\,$

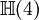
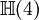
$\mathbb{H}(4)\,$

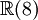
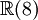
$\mathbb{R}(8)\,$

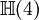
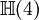
$\mathbb{H}(4)\,$

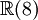
$\mathbb{R}(8)\,$

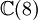
$\mathbb{C}(8)\,$

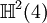
$\mathbb{H}^2(4)\,$

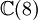
$\mathbb{C}(8)\,$

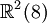
$\mathbb{R}^2(8)\,$

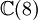
$\mathbb{C}(8)\,$

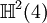
$\mathbb{H}^2(4)\,$

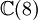
$\mathbb{C}(8)\,$

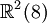
$\mathbb{R}^2(8)\,$

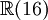
$\mathbb{R}(16)\,$

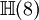
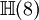
$\mathbb{H}(8)\,$

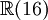
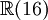
$\mathbb{R}(16)\,$

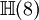
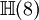
$\mathbb{H}(8)\,$

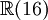
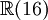
$\mathbb{R}(16)\,$

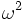
$\omega^2\,$

Il existe une toile embrouillée de symétrie et de relations dans la table ci-dessus. Par exemple, la table entière est symétrique par rapport à la colonne 1 (aussi bien que la colonne 5, - 3 et - 7). Se déplacer sur 4 emplacements dans n'importe quelle ligne donne une algèbre identique.

Voir aussi

Représentations des algèbres de Clifford

Portail des mathématiques

Ce document provient de « Classification des alg%C3%A8bres de Clifford ».

Catégorie : Algèbre

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Classification Des Algèbres De Clifford de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Classification des algebres de Clifford — Classification des algèbres de Clifford En mathématiques, en particulier dans la théorie des formes quadratiques non dégénérées sur les espaces vectoriels réels et complexes, les algèbres de Clifford de dimension finie ont été complètement… … Wikipédia en Français
Classification des algèbres de clifford — En mathématiques, en particulier dans la théorie des formes quadratiques non dégénérées sur les espaces vectoriels réels et complexes, les algèbres de Clifford de dimension finie ont été complètement classées. Dans chaque cas, l algèbre de… … Wikipédia en Français
Classification des algèbres de Clifford — En mathématiques, en particulier dans la théorie des formes quadratiques non dégénérées sur les espaces vectoriels réels et complexes, les algèbres de Clifford de dimension finie ont été complètement classées. Dans chaque cas, l algèbre de… … Wikipédia en Français
Algebre de Clifford — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algèbre De Clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
Algèbre de Clifford — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être… … Wikipédia en Français
Algèbre de Clifford du plan euclidien) — Algèbre de Clifford En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des… … Wikipédia en Français
Algèbre de clifford — En mathématiques, les algèbres de Clifford sont des algèbres associatives importantes au sein des théories des formes quadratiques, des groupes orthogonaux et en physique. Elles peuvent être vues comme l une des généralisations possibles des… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Classification Des Algèbres De Clifford