Cerf-volant (géométrie)
- Cerf-volant (géométrie)
-
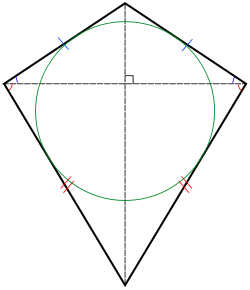
Un cerf-volant avec ses côtés égaux et son cercle inscrit.
En géométrie, un cerf-volant, est un quadrilatère dont une des diagonales est un axe de symétrie (ou -ce qui est équivalent- un quadrilatère ayant deux paires de côtés adjacents égaux). Les diagonales peuvent se couper à l'intérieur (cerf-volant convexe) ou à l'extérieur (« pointe de flèche » ou cerf-volant non convexe). Ceci contraste avec un parallélogramme, où les côtés égaux sont opposés. L'objet géométrique est nommé en référence au cerf-volant que l'on fait voler, qui a, dans son aspect le plus simple, cette forme.
Propriétés
Les paires de côtés égaux impliquent beaucoup de propriétés :
- Les diagonales sont perpendiculaires entre elles
- Une des diagonales divise le cerf-volant en deux triangles isocèles ; et l'autre le divise en deux triangles congrus
- Les cerf-volants possèdent au moins un axe de symétrie ; cet axe est la diagonale qui divise en deux triangles congrus
- Un cerf-volant possède un cercle inscrit ; c’est-à-dire qu'il existe un cercle qui est tangent aux quatre côtés.
- Si d1 et d2 sont les longueurs des diagonales, alors l'aire est

- Alternativement, si a et b sont les longueurs des côtés, et θ l'angle entre les côtés inégaux, alors l'aire est

Cas particuliers
- Lorsque le cerf-volant est concave, il devient une pointe de flèche, plutôt qu'un cerf-volant.
- Si tous les côtés sont de la même longueur, le quadrilatère est appelé un losange.
Voir aussi
Liens externes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Cerf-volant (géométrie) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Cerf-volant (Géométrie) — Pour les articles homonymes, voir Cerf volant (homonymie). Un cerf volant avec ses cotés égaux et son cercle inscrit. En géométrie … Wikipédia en Français
Cerf-volant (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Cerf volant Cerf volant : engin volant Cerf volant : quadrilatère particulier, en géométrie Voir aussi Expérience du cerf volant de… … Wikipédia en Français
Cerf-volant (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Cerf volant Cerf volant, engin volant Cerf volant, quadrilatère particulier, en géométrie Voir aussi Expérience du cerf volant de Franklin, célèbre… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Pavage de penrose — Les pavages de Penrose sont des pavages du plan découverts par le mathématicien et physicien britannique Roger Penrose dans les années 70. Ce sont des pavages non périodiques caractérisables par des règles locales : s ils ne sont… … Wikipédia en Français
Pavage de Penrose — Les pavages de Penrose sont des pavages du plan découverts par le mathématicien et physicien britannique Roger Penrose dans les années 1970. Ce sont des pavages non périodiques caractérisables par des règles locales : s ils ne sont… … Wikipédia en Français
Quadrilatère — Pour les articles homonymes, voir Quatre coins. Quadrilatères ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
Quadrilatere — Quadrilatère QUADRILATÈRES ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
Quadrilatère (mathématiques élémentaires) — Quadrilatère QUADRILATÈRES ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
Quadrilatère convexe — Quadrilatère QUADRILATÈRES ┌─────────────┼─────────────┐ concave convexe croisé … Wikipédia en Français
 Pour les articles homonymes, voir Cerf-volant (homonymie).
Pour les articles homonymes, voir Cerf-volant (homonymie).


